За период модуляции состояние системы меняется в зависимости от состояния силовых ключей. Поэтому на разных интервалах времени (интервалах коммутации) существует своя конфигурация и своя система дифференциальных уравнений, описывающих ее состояние. Таким образом, преобразователь является системой с переменной структурой, анализ которой классическими методами вести очень сложно и трудоемко. Наиболее эффективным методом является метод прямого имитационного моделирования на компьютере. Однако поиск оптимальных параметров системы регулирования может занять определенное время (в зависимости от сложности системы и квалификации специалиста) и потребовать создания специального алгоритма и программы поиска.

Для упрощения анализа и определения характеристик дискретно-непрерывной системы возможна ее замена на эквивалентную непрерывную систему при условии частота среза сглаживающего фильтра значительно ниже (примерно на порядок), чем частота коммутации. Используется метод усреднения переменных состояния, который дает решение, обеспечивающее компромисс между точностью и простотой.

Требования к системе регулирования. Качество регулирования.

Можно выделить три основных требования к системе регулирования:

1. Устойчивость – свойство системы автоматического регулирования возвращаться к первоначальному состоянию после прекращения действия внешнего возмущения. Система должна оставаться устойчивой на всех режимах;

Формальное определение внутренней устойчивости было введено в работах Александра Михайловича Ляпунова, поэтому такое понятие устойчивости принято называть устойчивостью по Ляпунову.

Система называется устойчивой по Ляпунову в положении равновесия x*, если при начальном отклонении от положения равновесия x* не более, чем на δ, траектория движения отклоняется от x* не более, чем на ε, причем для каждого ε можно найти соответствующее ему δ (ε ) :

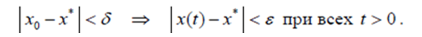
Фактически это означает, что чем меньше начальное отклонение, тем меньше траектория движения отклоняется от положения равновесия. Если вектор состояния стремится к положению равновесия, то есть, x(t) − x* →0 при t →∞, система называется асимптотически устойчивой в положении равновесия x*.

2. Точность - степень приближения истинного значения регулируемой величины к ее заданному значению в установившемся режиме. При этом ошибка не должна превышать допустимого значения.

Точность регулирования задается как допустимая ошибка регулирования (обычно в % к заданному или установившемуся значению этой величины)

3. Качество переходных процессов – при смене заданного значения система должна переходить в нужное состояние по возможности быстро и плавно.

В совокупности эти три требования определяют качество регулирования. Можно выделить три основные группы основных критериев качества:

1.Критерии точности – в качестве критерия используют величину ошибки в типовых режимах:

- Ненулевое, неподвижное (стационарное) состояние.

- Движение с постоянной скоростью.

- Движение с постоянным ускорением.

- Движение по гармоническому закону

2.Критерии запаса устойчивости – оценивают удаленность САР (системы автоматического регулирования) от границы устойчивости.

3.Критерии быстродействия – оценивают быстроту реагирования САР на изменение задающего или на появление возмущающего воздействий.

Существуют три основных подхода к оценке качества регулирования:

1.Определение качества по переходной характеристике (реакции системы на единичный ступенчатый входной сигнал или реакция системы на возмущающее воздействие – сброс/наброс нагрузки).

2. Оценка качества по частотным свойствам системы регулирования.

3. Оценка качества по расположению нулей и полюсов передаточной функции замкнутой системы регулирования, так называемая корневая оценка качества.