Сервисные центры в большинстве случаев предназначены для выполнения работ по концентрации, комплектации или разукрупнению грузопотоков.
Требуется:
а) определить оптимальный объем работы сервисного центра;
б) определить число сервисных центров на полигоне обслуживания.
Исходные данные:
- суммарный объем перевозок Q =300 тонн/сутки;
- удельная стоимость накопления, хранения и комплектации схр=10 руб/тонн;
- тариф на перевозку стр = 0,11 руб/ткм;
- административные расходы, связанные с содержанием одного сервисного центра са=22руб/сутки;
- средняя плотность грузообразования на полигоне d=0,1 т/км2;
- затраты на информационное сопровождение одной партии груза си=0,6 руб;
- размер партии поставки q =35 тонн.
Решение.
Объем работы и число сервисных центров определяется исходя из минимума общих затрат С, состоящих из:
- затрат, связанных с содержанием сервисного центра Са;
- затрат, связанных с хранением, накоплением и комплектацией
- затрат на перевозку Стр;
- затрат на оформление документов и передачу информации Си.
Общие затраты С определяются путем суммирования всех этих затрат:
С = Схр+Са + Си+Стр (6.1)
Затраты, связанные с хранением, накоплением и комплектацией определяют по формуле:
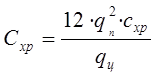 (6.2)
(6.2)
где 12 - параметр накопления груза в случае равномерного поступления грузопотока;
qn - размер партии поставки, тонн;
q ц - объем работы одного сервисного центра, тонн.
Затраты, связанные с функционированием и содержанием сервисных центров определяют по формуле:
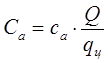 (6.3)
(6.3)
Затраты на оформление документов и передачу информации рассчитывают по формуле:
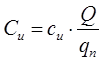 (6.4)
(6.4)
Затраты на перевозку определяются по формуле:
Cmp = cmpQ , (6.5)
Где - среднее расстояние перевозки в км, определяется из предположения, что плотность грузообразования d - величина равномерная и для каждого сервисного центра полигон имеет форму круга радиуса r = 2/3 R , где R - радиус полигона обслуживания.
В этом случае плотность грузообразования в зоне обслуживания сервисного центра определяют по формуле:
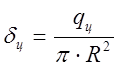 (6.6)
(6.6)
Определив из формулы (6.6) R и подставив полученное значение в формулу (6.5), получим:
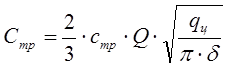 (6.7)
(6.7)
Подставив полученные зависимости для определения слагаемых в формулу (6.1), получим аналитическую зависимость для определения суммарных затрат:
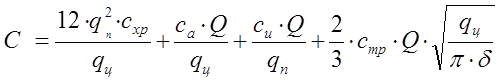 (6.8)
(6.8)
Для определения минимума функции общих затрат найдем ее первую производную по 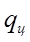 и приравняем ее нулю:
и приравняем ее нулю:

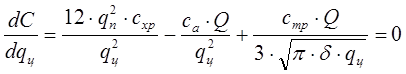 (6.9)
(6.9)
Отсюда
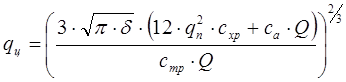 (6.10)
(6.10)
Подставив значения переменных в выражение (6.10), получим оптимальный объем работы одного сервисного центра:
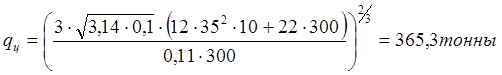
Число сервисных центров Z определяется по формуле:
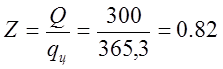
При этом общие затраты составляют:
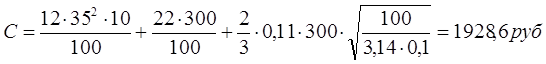
Величина общих затрат в зависимости от объема работы одного сервисного центра может быть представлена в виде графика. Для этого, используя заданные параметры, рассчитаем общие затраты при изменении q ц в пределах от 80 до 200 тонн. Результаты расчетов приведены в таблице 6.1.
Таблица 6.1 - Зависимость общих затрат от q ц
| q ц , тонн | Объем работы в тоннах | ||||||||
| 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | |
| С,руб | 1929 | 1505 | 1323 | 1235 | 1192 | 1173 | 1169 | 1174 | 1185 |
Дата: 2019-05-28, просмотров: 756.