Портфели, оптимальные в смысле задачи Марковица, называются эффективными портфелями (efficient portfolios) рисковых ценных бумаг или оптимальными по Марковицу портфелями.
Осуществим качественный анализ решения задачи Марковица и сформулируем некоторые свойства оптимальных портфелей.
1. Согласно (39) с увеличением ожидаемой доходности портфеля вклады { 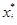 } в ценные бумаги при возможности операции "короткая продажа" изменяются линейно: увеличиваются для более доходных и уменьшаются для менее доходных активов. Известно, что при невозможности операции "короткая продажа" имеет место кусочно-линейное изменение {
} в ценные бумаги при возможности операции "короткая продажа" изменяются линейно: увеличиваются для более доходных и уменьшаются для менее доходных активов. Известно, что при невозможности операции "короткая продажа" имеет место кусочно-линейное изменение { 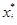 }[17].
}[17].
2. Из (43) следует, что риск оптимального портфеля возрастает вместе с ростом ожидаемой доходности. При возможности операции "короткая продажа" достижима сколь угодно высокая доходность при соответственно растущем риске. При невозможности данной операции максимальной доходностью обладает портфель, образованный из актива (активов) с максимальной ожидаемой доходностью (на рис. 4 такому портфелю соответствует точка А и доходность 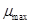 ).
).
Таким образом, из (43) следует, что функция 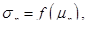 описывающая зависимость между риском и доходностью оптимальных портфелей, является вогнутой и имеет положительный наклон (см. рис. 4). Причем если
описывающая зависимость между риском и доходностью оптимальных портфелей, является вогнутой и имеет положительный наклон (см. рис. 4). Причем если 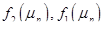 -функции, соответствующие предположениям о возможности и невозможности операции "короткая продажа", то имеет место соотношение
-функции, соответствующие предположениям о возможности и невозможности операции "короткая продажа", то имеет место соотношение 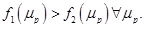 Это означает, что при использовании операции "короткая продажа" всегда можно построить более эффективный портфель за счет решения задачи оптимизации на более широком множестве портфелей. Иллюстрацией данному свойству служит рис. 4.
Это означает, что при использовании операции "короткая продажа" всегда можно построить более эффективный портфель за счет решения задачи оптимизации на более широком множестве портфелей. Иллюстрацией данному свойству служит рис. 4.
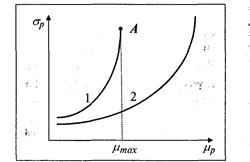
Рис. 4. Графики зависимости риска эффективного портфеля от его ожидаемой доходности при возможности (2) и невозможности (1) операции "короткая продажа"
В теории портфельного инвестирования зависимость между риском и доходностью оптимальных портфелей обычно анализируется в системе координат "доходность — риск", причем по оси абсцисс откладываются значения риска, а по оси ординат - значения ожидаемой доходности портфеля. Поэтому далее будем использовать именно такое расположение координат.
3. Эффективный портфель рисковых ценных бумаг с характеристиками:
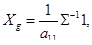 (44)
(44)
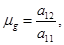 (45)
(45)
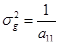 (46)
(46)
будем называть "глобальным" эффективным портфелем (global mean-variance portfolio [37] ), на рис. 5 ему соответствует точка G.
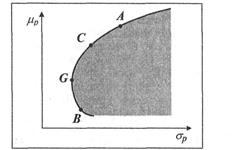
Рис. 5. Фронт эффективных портфелей:
А, С- эффективные портфели; G- "глобальный" эффективный портфель; В - неэффективный портфель
4. Эффективные портфели обладают двумя свойствами оптимальности
1) имеют максимальную доходность среди всех достижимых портфелей с одинаковым риском (например, если А -эффективный портфель с характеристиками 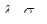 то для любого достижимого портфеля с характеристиками
то для любого достижимого портфеля с характеристиками 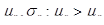 при
при 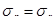 ) ;
) ;
2) имеют минимальный риск среди всех достижимых портфелей с одинаковой доходностью (если С - эффективный портфель с характеристиками 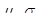 , то для любого достижимого портфеля с характеристиками
, то для любого достижимого портфеля с характеристиками 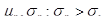 при
при 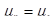 ).
).
Справедливы также следующие два свойства ковариаций доходностей портфелей активов[18]:
4.Ковариация доходностей Ra, Rc двух эффективных портфелей А и С с ожидаемыми доходностями 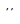 и
и 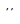 равна:
равна:
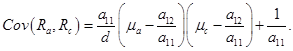 (47)
(47)
6. Ковариация доходности глобального эффективного портфеля Rg с доходностью любого другого портфеля или актива Ra равна:
Cov(Ra,Rg)= 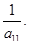
Множество всех эффективных портфелей с характеристиками 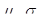 в системе координат "доходность — риск" описывается кривой, известной как фронт эффективных портфелей (efficient frontier), ограничивающей множество всех портфелей, достижимых на множестве из N ценных бумаг с характеристиками
в системе координат "доходность — риск" описывается кривой, известной как фронт эффективных портфелей (efficient frontier), ограничивающей множество всех портфелей, достижимых на множестве из N ценных бумаг с характеристиками 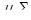 (feasible set).
(feasible set).
На рис 5 фронту эффективных портфелей соответствует отрезок кривой от точки G (включая "глобальный" портфель G) до точки А и выше. Портфели, лежащие на отрезке кривой от точки G до точки В и ниже, не являются эффективными. Портфели, лежащие в заштрихованной области, ограниченной кривой (включая саму кривую), образуют множество достижимых портфелей (feasible set).
Таким образом, в результате решения задачи Марковица инвестор получает не один, а бесконечное множество эффективных портфелей. Индивидуальные предпочтения инвестора при выборе единственного оптимального в смысле подхода "доходность — риск" портфеля могут быть учтены с использованием кривых безразличия данного инвестора. Проиллюстрируем этот выбор на примере.
Пусть приемлемые для инвестора портфели, соответствующие различным уровням его притязаний, описываются кривыми безразличия 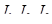 (рис. 6).
(рис. 6).
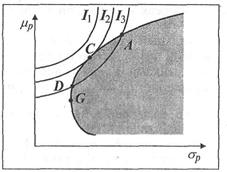
Рис. 6. Выбор оптимального портфеля с учетом предпочтений инвестора, задаваемых кривыми безразличия
Фронту эффективных портфелей соответствует кривая G-A. Очевидно, портфели, принадлежащие кривой безразличия 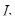 , недостижимы. Среди достижимых и приемлемых для инвестора портфелей эффективными являются портфели А, С и D. Но более эффективным среди них является портфель С, поскольку он лежит на кривой безразличия
, недостижимы. Среди достижимых и приемлемых для инвестора портфелей эффективными являются портфели А, С и D. Но более эффективным среди них является портфель С, поскольку он лежит на кривой безразличия 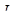 что выше и левее кривой
что выше и левее кривой 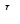 .
.
Таким образом, оптимальным для конкретного инвестора является портфель С, соответствующий точке касания фронта эффективных портфелей и кривой безразличия данного инвестора.
Подход Г. Марковица, ядром которого является идея диверсификации вложений, можно рассматривать как теорию портфельного инвестирования в ее микроэкономическом аспекте, поскольку основным объектом исследования в рамках данной теории является портфель инвестора, формируемый им на основе индивидуальных представлений относительно ожидаемой доходности и риска ценных бумаг.
Дата: 2019-05-28, просмотров: 318.