Портфелем ценных бумаг (portfolio of securities) инвестора будем называть совокупность ценных бумаг, принадлежащих данному инвестору[13].

Пусть инвестор формирует свой портфель на множестве из N(N>1) различных ценных бумаг. Капитал инвестора распределяется между различными активами в некоторых пропорциях х1, x2, ..., xN, удовлетворяющих условию:

Х1 + Х2 + ... + XN = 1. (26)

Совокупность величин {хi} (i=1, 2, ..., N) определяет структуру портфеля ценных бумаг. Имеет место следующая интерпретация значений {хi}:

а) хi >0 означает, что доля хi- капитала инвестора вложена в ценную бумагу i;

б) хi =0 означает, что ценная бумага i отсутствует в портфеле инвестора;

в) хi <0 означает, что относительно ценной бумаги i совершена операция короткая продажа (short sale); средства, полученные за счет данной операции, составляют долю |хi| от первоначального капитала инвестора и использованы им для покупки других ценных бумаг.

Определим векторы: Х=(хi) (i=1, 2, ..., N) - вектор, определяющий структуру портфеля; 1=(1, 1, ..., 1)т - единичный N-вектор. Тогда условие (5.1) может быть представлено в виде:

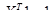 (27)

Для характеристик ценных бумаг, соответствующих одному и тому же периоду владения, введем следующие обозначения:

R=(Ri) - вектор доходностей ценных бумаг, образующих портфель, причем компонента Ri (i=1, 2, ...,N) данного вектора представляет собой "простую" ставку доходности ценной бумаги за один период владения.

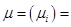E(R) - вектор ожидаемых доходностей ценных бумаг, т.е. 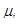=Е(Ri)>0 (i=1, 2, ..., N) - ожидаемая доходность ценной бумаги i за один период владения;

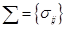=E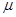((R- )(R— 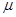)T) (i, j=1, 2, ..., N) - ковариационная матрица доходностей ценных бумаг размерности (NxN). Матрица  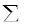является симметричной, т.е. 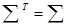. Будем также предполагать, что она является невырожденной: 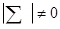. Диагональные элементы матрицы  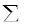представляют собой дисперсии доходностей активов:

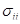=D(Ri)=

Для удобства будем также использовать обозначение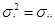

Среднеквадратическое отклонение 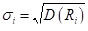> О доходности ценной бумаги i будем интерпретировать как риск ценной бумаги.

Недиагональные элементы матрицы 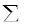 являются коварициями доходностей ценных бумаг и определяются по формуле

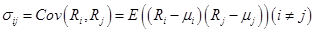
и связаны с коэффициентами корреляции доходностей 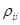 соотношением:

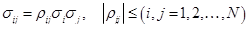. (28)

С учетом принятых обозначений и соглашений характеристики портфеля ценных бумаг для одного периода владения будут определяться следующими выражениями:

• доходность портфеля:

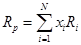; (29)

• ожидаемая доходность портфеля:

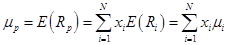 (30)

• дисперсия доходности портфеля:

.

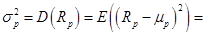
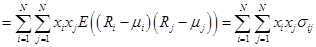Откуда получаем:

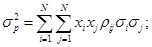 (31)

• риск портфеля:

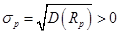 (32)

В аналитических исследованиях более удобной является векторно-матричная форма представления характеристик портфеля:

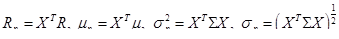 (33)

Пусть инвестор распределяет свой капитал среди N (N>1) рисковых активов в некоторых пропорциях Как известно, в рамках подхода "доходность — риск", предполагается, что цены { 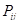}, а следовательно, и доходности активов {Rit} ( 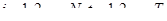) являются случайными величинами. Из доходностей N активов за один и тот же период t образуем вектор доходностей Rt = 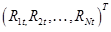а из величин { 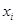} - вектор, определяющий структуру портфеля X=(xh x2, ...,xN)T.

Решение задачи формирования оптимального в смысле подхода "доходность — риск" портфеля основано на определенных модельных предположениях относительно:

• вероятностной модели доходностей (курсов) активов

• рынка и поведения его участников.

1) Предположения относительно вероятностной модели доходностей.

Уже обсуждались традиционные предположения относительно вероятностной модели доходностей в задаче оптимального портфельного инвестирования. Так же отмечались недостатки этих предположений с точки зрения адекватности соответствующей им модели.

В соответствии с этими предположениями, значения векторов доходностей {Rt}, полученные за анализируемый исторический период, можно рассматривать как случайную выборку из многомерного нормального распределения, параметрами которого являются математическое ожидание вектора доходностей активов (т.е. вектор ожидаемых доходностей) 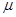, и ковариационная матрица вектора доходностей активов 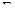. Это позволяет не учитывать автокорреляцию значений доходностей и считать ожидаемые доходности активов, дисперсии и ковариации (ковариационную матрицу) доходностей активов постоянными во времени, т.е. полагать, что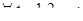

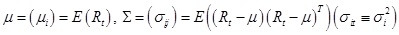
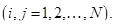
В качестве статистических оценок параметров 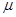 и 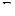 при этом теоретически могут использоваться выборочное среднее значение  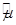и выборочная ковариационная матрица 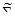. На практике, однако, как это будет показано, для оценивания неизвестных параметров приходится использовать различные «факторные» модели.

Найденные оценки 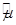,  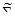рассматриваются как прогнозные значения соответствующих характеристик в будущем периоде владения и используются вместо неизвестных истинных значений параметров в алгоритмах оптимизации структуры портфеля ценных бумаг для одного будущего периода владения, т.е. решаются однопериодные задачи оптимизации структуры портфеля активов для каждого периода владения независимо от других периодов.

2) Предположения относительно рынка и поведения его участников.

Данные предположения состоят в следующем:

М.1. Инвесторы осуществляют оценку портфелей, основываясь на ожидаемой доходности и риске активов.

М.2. При выборе их двух идентичных во всем, кроме ожидаемой доходности, портфелей инвестор отдает предпочтение портфелю с большей ожидаемой доходностью.

М.3. При выборе из двух идентичных во всем, кроме риска, портфелей инвестор отдает предпочтение портфелю с меньшим риском.

М.4. Характеристики активов и портфелей относятся к одному заданному периоду владения.

М.5. Активы являются бесконечно делимыми, т.е. в каждый актив может быть вложена любая доля капитала инвестора.

М.6. Отсутствуют какие – либо технические препятствия в реализации оптимальных инвестиционных стратегий; относительно любого актива возможна операция «короткая продажа»; налоги и издержки, связанные с покупкой и продажей активов, не принимаются во внимание.

При выполнении свойства М.6 рынок часто называется полным рынком (complete market)[14].

Предположения М.1 – М.3 выражают предпочтения инвесторов в рамках подхода «доходность – риск». Предположение М.4 говорит о том, что рассматривается однопериодная задача оптимизации. Предположения М.5 – М.6 носят технический характер и вводятся для упрощения аналитического решения задачи.

3) Постановка задачи оптимизации структуры портфеля.

Пусть инвестор формирует свой портфель сроком на один период владения из N (N>1) различных рисковых ценных бумаг. Прогнозные значения вектора ожидаемых доходностей активов и ковариационной матрицы доходностей активов для рассматриваемого периода равны 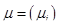 и 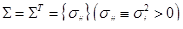. Будем полагать, что  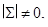т.е. ковариационная матрица  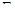является невырожденной (положительно определенной как ковариационная матрица). Приемлемая для инвестора доходность портфеля ценных бумаг равна .

Задача заключается в определении такой структуры портфеля 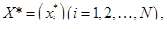 которая обеспечила бы достижение заданной доходности портфеля  с минимальным риском. Математическая формулировка данной задачи имеет вид:

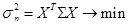, (34)

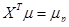, (35)

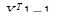 (36)

Соотношения (35)—(36) представляют собой формализованное описание задачи определения оптимального в смысле подхода "доходность — риск" портфеля рисковых ценных бумаг, которая известна как задача Марковица[15].

Вектор X*, являющийся решением задачи Марковица, определяет структуру оптимального в смысле подхода "доходность — риск" портфеля среди всех возможных портфелей с ожидаемой доходностью 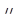. Заметим, что в рассматриваемом случае компоненты вектора 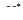=( 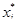) могут принимать отрицательные значения, что означает рекомендацию инвестору совершить относительно соответствующих активов операцию "короткая продажа".

Множество возможных или достижимых портфелей (feasible set) в данном случае - это множество всех портфелей, которые можно образовать из N рассматриваемых ценных бумаг при возможности использования операции "короткая продажа ".