Во многих практических задачах, например при покупке или продаже облигаций на фьючерсных рынках, появляется необходимость в определении стоимости и ожидаемой доходности облигаций в будущие периоды.
В связи с этим возникает еще один тип процентных ставок, известных как форвардные ставки.
1) Форвардные ставки.
Форвардными ставками (forward rates) в широком смысле принято называть ставки, которые фиксируются в текущий момент относительно займов или кредитов, которые должны быть получены или предоставлены в некоторый будущий период.
Применительно к долговым ценным бумагам под форвардной ставкой будем иметь в виду ставку, которая устанавливается в текущий момент и характеризует доходность к погашению ценной бумаги, соответствующую некоторому будущему периоду владения.
Обозначим: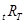 
- ставка доходности к погашению в периоде t бескупонной облигации со сроком обращения, равным Т-периодам.
Пусть известна временная структура процентных ставок в виде последовательности спот-ставок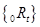 
, t=l, 2, ..., Т. Тогда ставки 
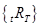, удовлетворяющие условию
(1+0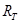 
)Т= 
, 
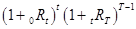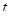=1, 2, ..., Т-1, Т>1, (22)
называются форвардными.
Заметим, что условие (22) - это условие эквивалентности двух альтернативных стратегий инвестирования, исключающее возможность получения гарантированного дохода без каких-либо инвестиций, т.е. исключающее арбитражные возможности
Первая стратегия (ей соответствует правая часть соотношения (22)) заключается в инвестировании средств сначала на t периоды, а затем реинвестировании полученной суммы на оставшийся до погашения срок, равный T-t периодам владения. На первом и втором этапах инвестирования используются соответственно спот-ставка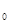 
Rt для 
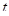-периодных вложений и форвардная ставка t 
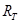, соответствующая периоду t. Вторая стратегия (левая часть соотношения (22)) состоит в инвестировании средств сразу на весь срок, оставшийся до погашения облигации под ставку 
.
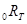Из соотношения (22) может быть найдено представление для форвардных ставок в случае капитализации дохода с использованием формулы сложных процентов. Это представление определяется формулой (23), которая позволяет вычислить по заданным значениям спот-ставок {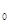 
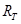}, а также комбинациям значений t и Т все необходимые для анализа форвардные ставки:
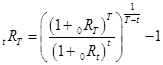(23)
В случае непрерывно начисляемых процентов с учетом обозначения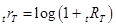 
получаем:
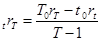
С учетом (20), (22) текущая стоимость купонной облигации может быть представлена в виде
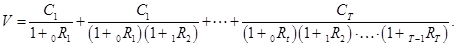(24)
Воспользуемся формулами (23) и (24) для нахождения форвардных цен облигаций, т.е. ожидаемых в текущий момент цен облигаций в будущие периоды.
2) Форвардные цены облигаций.
Пусть Vt (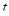 
=1, 2, ..., Т) - цена облигации в конце t-гo периода владения после выплат по ней всех предусмотренных платежей. Поскольку данные цены соответствуют будущим периодам времени, их принято называть форвардными ценами облигации.
Форвардные цены V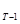 
,..., V 
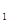для Т-периодной купонной облигации при известных форвардных ставках { 
) ( 
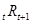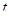=l, 2, ..., T-l) могут быть определены с помощью следующей рекуррентной формулы:
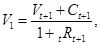
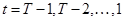(25)
Рекуррентная формула (25) основывается на интерпретации текущей стоимости ценной бумаги как некоторой суммы, которая может быть вложена на определенный срок под соответствующую данному сроку и риску вложений ставку. Предполагается, что полученная по окончании срока вложений сумма будет равна стоимости потока платежей по ценной бумаге, представленного на рис. 2
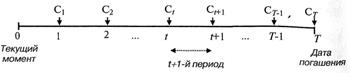
Рис. 2. Схема потока платежей по облигации
В соответствии с указанным принципом стоимость облигации после ее погашения в момент времени Т равна нулю, поскольку после погашения по облигации не ожидается никаких платежей. Таким образом, можно положить Vт=0.
В начале последнего периода по облигации ожидается платеж, равный Ст, поэтому в момент времени Т-1 стоимость облигации должна удовлетворять соотношению:
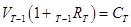
Откуда следует:
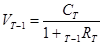
Для цены облигации в момент времени Т-2 (т.е. в начале Т-1-го периода) имеем:
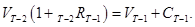
Аналогично для момента времени t, являющегося началом произвольного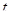 
+1-го периода ( 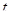= Т-1, Т-2, ..., 1), получаем:
Vt (1+tRt+l)=Vt+1+ Сt+1,
что влечет (25).
При 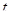=0 формула (25) эквивалентна формуле (24) и приводит к вычислению текущей стоимости облигации. Приведем некоторые частные случаи формулы (25):
•для купонных облигаций с потоком платежей вида C1=qF, t=l, 2, ...,Т-1; CТ=qF+F получаем выражение вида:
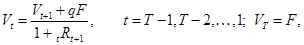
где с целью сохранения общности формально положено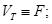 
•для бескупонных облигаций, полагая в предыдущем выражении q=0, получаем:
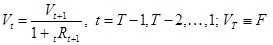
3) Интерпретация кривой доходности.
Форвардные ставки существенно используются в рамках различных теорий временной структуры процентных ставок. Например, в соответствии с теорией чистых ожиданий при отсутствии на рынке арбитражных возможностей устанавливаемые в текущий момент форвардные ставки для будущих периодов должны быть равны ожидаемым в соответствующих будущих периодах спот-ставкам с аналогичными сроками инвестирования. Другими словами (используя терминологию вероятностного подхода ), форвардные ставки должны равняться математическому ожиданию соответствующих спот-ставок.
На данном предположении основана интерпретация формы кривой доходности в рамках теории чистых ожиданий. В качестве примера рассмотрим две стратегии инвестирования на два периода. Первая заключается в покупке двухпериодной бескупонной облигации, доходность к погашению которой определяется спот-ставкой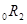 
. Вторая стратегия представляет собой так называемую стратегию возобновления (rollover strategy) и состоит в последовательной покупке однопериодных бескупонных облигаций. Доходность к погашению первой однопериодной облигации определяется однопериодной спот-ставкой 
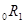, а доходность второй облигации - форвардной однопериодной ставкой 
.
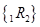Предположение об отсутствии арбитражных возможностей приводит по аналогии с (22) к тождеству
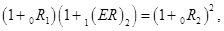
в котором, в соответствии с теорией чистых ожиданий учтено, что форвардная ставка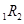 
равна ожидаемой в будущем периоде спот-ставке 
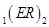- Представим данное соотношение в более удобном для интерпретации виде:
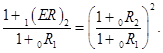(26)
На основании (26) можно сделать следующие выводы о форме кривой доходности (см. рис. 1):
1) если кривая доходности имеет наклон вверх, т.е.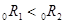 
, то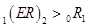 
.. Это означает, что инвесторы ожидают в будущем периоде роста краткосрочных (однопериодных) ставок;
2) если кривая доходности имеет наклон вниз, т.е.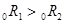 
, то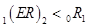 
, а значит, инвесторы ожидают в будущем периоде падения краткосрочных ставок;
3) если кривая доходности параллельна оси абсцисс, т.е.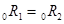 
, то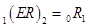 
, и, следовательно, в будущем инвесторы ожидают, что краткосрочные ставки не изменятся.
Очевидно, аналогичные рассуждения могут быть проведены и для произвольного срока инвестирования.
Оценка рисков
Как отмечалось ранее, инвестиции в ценные бумаги в условиях неопределенности сопряжены с риском того, что фактическая доходность вложений может отличаться от ожидаемой доходности. Это дает основание рассматривать доходность R ценной бумаги, соответствующую некоторому периоду владения, как случайную величину, а выбор инвестиционной стратегии осуществлять на основе анализа ее числовых характеристик: математического ожидания, дисперсии, среднеквадратического отклонения и т.д. При этом математическое ожидание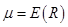 
доходности актива соответствует ожидаемой доходности, а дисперсия 
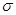2=D(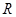 
) или сред-неквадратическое отклонение 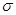доходности могут использоваться как меры риска вложений в данный актив.
Идеальной для инвестора стратегией инвестирования в рамках данного подхода была бы стратегия, обеспечивающая достижение максимальной ожидаемой доходности при минимальном риске вложений. Однако одновременное достижение этих целей невозможно. Практика работы на финансовых рынках свидетельствует о том, что большему значению ожидаемой доходности обычно сопутствует и большее значение риска вложений.
Риск и доходность связаны тесной однонаправленной зависимостью, что вполне логично, так как любой инвестор требует от более опасных проектов адекватной добавочной прибыли. Величина этой надбавки слабо меняется со временем, что позволяет использовать ее определения стоимости стандартных пакетов бизнесов, например на фондовом рынке. Однако очень часто требуется проанализировать совершенно конкретный проект, имеющий нестандартные риски, в этом случае вопрос измерения этих рисков выходит на передний план. Для того чтобы их определить, мы должны знать[8]:
· как измерить риск
· какова связь между возникновением риска и требуемыми премиями за риск.
Один из способов охарактеризовать неопределенность — сказать, что событий происходит меньше, чем можно ожидать. Риск, присущий активам, можно точно выразить описанием всех возможных результатов и вероятности, их возникновения. Однако для реальных активов это сделать трудно, а часто и невозможно. Поэтому стандартными статистическими показателями разброса результатов (а следовательно, порождаемой им неопределенности) служат дисперсия и стандартное отклонение. Дисперсия рыночной доходности представляет собой ожидаемое отклонение от ожидаемой доходности в квадрате. Это можно выразить иначе:
Дисперсия σ2 =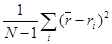 
, где ri - фактическая доходность, rср - ожидаемая доходность. Стандартное отклонение равно квадратному корню из дисперсии: стандартное отклонение σ =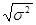 
Эти показатели и являются естественными измерителями риска. Если бы исход с события был предопределен, стандартное отклонение равнялось бы нулю. Как мы определим позже, дисперсия и стандартное отклонение служат верными критериями риска только при нормальном распределении доходностей. При этом следует иметь ввиду, что только стандартное отклонение имеет размерность исследуемого фактора, дисперсия же, теоретически более адекватно отражает степень разброса значений.
Инвестируя в активы с более высоким риском, инвесторы, как правило, рассчитывают на достижение "более высокой доходности в виде премии за риск (risk premium). Иллюстрацией этой закономерности могут служить данные, приведенные в табл. 1. Таблица содержит статистические оценки в виде выборочного среднего для ожидаемой годовой доходности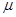 
,-и в виде выборочного среднеквадратического отклонения для риска 
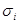, а также соответствующие значения коэффициента вариации для трех видов ценных бумаг фондового рынка США: казначейских векселей (T-bills), долгосрочных корпоративных облигаций (Long Term Corporate Bonds - LTCB's) и обыкновенных акций (Common Stocks - CS's).
Из приведенных данных следует, что большему значению ожидаемой доходности соответствует большее значение риска. Кроме того, анализ значений коэффициента вариации доходности ценных бумаг {Vi} показывает, что с ростом доходности растет и доля риска, приходящаяся на единицу доходности. Существование двух противоположных целей инвестирования позволяет сделать два важных вывода.
1. При осуществлении финансовых инвестиций в условиях неопределенности необходимо учитывать не только ожидаемую доходность, но и риск финансовых активов. При этом притязания инвесторов относительно доходности и риска должны быть сбалансированы.
2. Не следует вкладывать весь капитал в один актив. Действительно, вкладывая весь свой капитал лишь в один актив, инвестор обрекает себя либо на заведомо низкую доходность, либо на заведомо высокий риск. Следствием второго вывода является необходимость распределения (диверсификации) капитала между разными активами[9].
Распределение инвестируемого капитала среди различных ценных бумаг приводит к формированию портфеля ценных бумаг инвестора. За счет использования "эффектов портфеля" инвестор может достичь приемлемых для себя значений ожидаемой доходности и риска вложений. В этом состоит главное преимущество портфельного инвестирования по сравнению с инвестициями в отдельные ценные бумаги.
Выбор портфеля ценных бумаг на основе учета его ожидаемой доходности (mean) и риска (variance) известен как подход "доходность - риск" (mean-variance), который был впервые сформулирован Г. Марковицем. Дальнейшее развитие этот подход получил благодаря ранее упоминавшимся работам Дж. Тобина, У. Шарпа, С. Росса и др.
В рамках данного подхода предполагается, что инвестор стремится максимизировать ожидаемую доходность портфеля при заданном уровне риска либо минимизировать риск при заданном уровне ожидаемой доходности посредством диверсификации вложений. Для иллюстрации проблемы выбора портфеля ценных бумаг с помощью подхода "доходность — риск" удобно использовать кривые безразличия.
Кривые безразличия (indifference curves) - это линии, описывающие различные комбинации значений ожидаемой доходности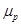 
и риска 
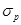портфелей ценных бумаг, которые являются равноценными в смысле определенных предпочтений инвестора (рис. 2).
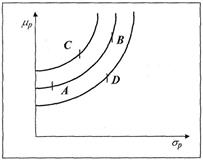
Рис. 2. Кривые безразличия инвестора при подходе "доходность — риск"
В рамках подхода "доходность - риск" используются следующие предположения относительно предпочтений инвестора[10]:
1) предположение о "ненасыщаемости" (nonsaturation) инвестора, которое может быть сформулировано следующим образом: при выборе из двух идентичных во всем, кроме ожидаемой доходности, портфелей инвестор отдает предпочтение портфелю с большей ожидаемой доходностью;
2) предположение о том, что инвестор избегает риска (risk aversion), т.е. при выборе из двух идентичных во всем, кроме риска, портфелей он отдает предпочтение портфелю с меньшим риском.
Избегать риска - значит идти на риск только при соответствующей компенсации за риск, т.е. "премии за риск": большему риску должен соответствовать больший доход. Например, инвестор, избегающий риска, не станет участвовать в "честной" азартной игре (fair game) типа подбрасывания монеты, ожидаемый доход от которой равен нулю.
Пусть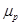 
- ожидаемая доходность, 
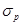— риск портфеля. В силу сделанных предположений относительно предпочтений инвестора в рамках рассматриваемого подхода соответствующие кривые безразличия в системе координат "доходность — риск" должны быть вогнутыми и иметь положительный наклон, как это имеет место на рис. 2.
Кривые безразличия инвестора обладают рядом свойств.
1. Каждая кривая линия описывает множество равноценных портфелей с характеристиками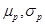 
соответствующими заданному уровню притязаний инвестора, и, следовательно, кривые безразличия одного инвестора не могут пересекаться.
2. Портфели, лежащие выше и левее, являются более привлекательными, чем портфели, располагающиеся ниже и правее. Так, изображенные на рис.2 портфели А и В являются равноценными, портфель С является более привлекательным, чем портфели А я В, а те, в свою очередь, привлекательнее портфеля D.
3. Каждый инвестор имеет бесконечно много кривых безразличия, т.е. ему соответствуют так называемые карты кривых безразличия.
4. Кривые безразличия для инвесторов, избегающих риска в различной степени, т.е. различающихся склонностью к риску, имеют различный угол наклона (рис. 3).
Рассмотрим задачу вычисления характеристик 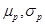портфеля ценных бумаг, а также исследуем эффекты портфельного инвестирования.
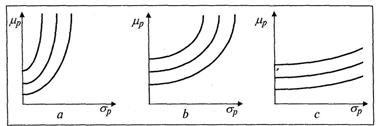
Рис. 3. Кривые безразличия инвесторов, различающихся склонностью к риску: а - невысокая склонность; b - средняя склонность; с - высокая склонность
Основываясь на вышеизложенном, можно сделать следующие выводы. В настоящее время существует достаточный теоретический аналитический аппарат, основанный на различных математических методах, позволяющих оценивать доходности и риски ценных бумаг.
В рамках рассмотренных классических постановок задач Марковица — Тобина предполагается, что инвесторы формируют оптимальные в смысле подхода "доходность -риск" портфели ценных бумаг сроком на один период владения, исходя из прогнозных значений ожидаемых доходностей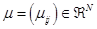 
и ковариационной матрицы доходностей 
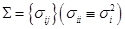на рассматриваемый период инвестирования. Прогнозные значения данных характеристик строятся на основе имеющихся "исторических" значений доходностей активов { 
} ( 
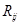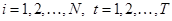) за предшествующие периоды времени. При этом предполагается, что параметры , 
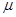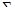остаются постоянными в течение всего анализируемого периода.
Государственные облигации используются инвесторами преимущественно для сохранения денежных средств, так как они имеют невысокую доходность, но и риск по ним тоже низок.
Дата: 2019-05-28, просмотров: 216.
