Оценка стоимости облигации

Как известно, облигации представляют широкий класс долговых ценных бумаг с ограниченным сроком обращения и фиксированным доходом. По сроку обращения различают краткосрочные, среднесрочные и долгосрочные облигации[5].

Краткосрочные облигации обычно являются бескупонными. При анализе их удобно рассматривать как однопериодные активы, доход по которым образуется за счет разницы цен покупки и продажи (погашения).

Облигации с более длительными сроками обращения обычно являются купонными, т.е. предусматривают периодические выплаты процентов (купонного дохода) в течение срока обращения и возврат номинальной стоимости облигации при погашении.

Менее типичным видом облигаций являются так называемые бессрочные облигации, т.е. облигации, погашение которых не ожидается в обозримом будущем. Примерами бессрочных облигаций (undated, irredeemable gilts) являются несколько типов государственных облигаций, обращающихся на фондовом рынке Великобритании. Наиболее известными среди них являются "2,5-процентные консоли" 1888 г. выпуска. Однако анализ подобных ценных бумаг представляет скорее теоретической интерес.

В настоящем разделе приводится краткое изложение методов анализа основных типов "многопериодных" облигаций в предположении полной определенности относительно потоков платежей по ним и ставок дисконтирования.

Анализ купонных облигаций

Для определения текущей стоимости купонной облигации воспользуемся общей формулой (1) при некоторых предположениях, учитывающих особенности потока платежей по купонным облигациям.

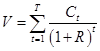(1)

Обозначим:

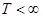 - количество периодов владения, оставшихся до погашения облигации;

F - финальная выплата по облигации (principal), совпадающая с ее номинальной стоимостью;

q>0 - ставка купонного дохода (купонная доходность) за один период владения в долях;

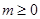 - частота выплат купонного дохода за один период владения;

R>0 - ставка дисконтирования купонного дохода, соответствующая одному периоду владения.

Ставка R интерпретируется как ожидаемая доходность вложений.

Относительно потока платежей 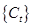 предполагается:

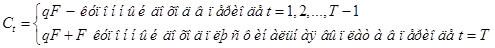
Предполагается также, что платежи в виде купонного дохода поступают в конце каждого периода и подлежат капитализации с начислением сложных процентов.

Рассмотрим вначале случай, когда 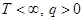 и 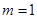, т.е. когда период выплат купонного дохода совпадает с периодом владения облигацией. С учетом сделанных предположений из (1) следует, что текущая стоимость купонной облигации определяется соотношением:

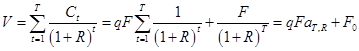(2)

Где:

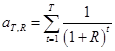(3)

- текущая стоимость ренты с Т единичными выплатами и постоянной ставкой наращения R;

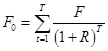(4)

- текущая стоимость финальной выплаты по облигации, .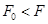

Обозначим 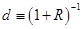 - дисконтный множитель. По формуле для суммы Т первых членов геометрической прогрессии имеем:

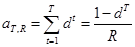(5)

На основании (3)—(5) из (2) следует:

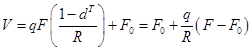(6)

Если известна текущая рыночная стоимость облигации (цена покупки) Р, то можно оценить инвестиционную привлекательность облигации на основе чистой текущей стоимости NPV и внутренней доходности R*, которая, как известно, является решением уравнения NPV=0, т.е. удовлетворяет тождеству:

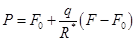(7)

Ставка внутренней доходности облигации R* определяет так называемую полную доходность облигации (доходность к погашению), поскольку учитывает все виды платежей по облигации до момента ее погашения.

Получить явное выражение для ставки R* в общем случае затруднительно, поскольку от нее зависит и величина Fq, поэтому выполним качественный анализ формулы (7).

На основании (7) можно сделать следующие выводы:

• рыночная цена купонной облигации прямо пропорциональна ставке купонного дохода q, причем P>F0 для q>0;

• существует обратная зависимость между рыночной ценой облигации (ценой покупки) и ее доходностью R*.

Для купонных облигаций с несколькими выплатами купонного дохода в течение одного периода владения (т.е. при 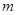>1) может быть проведен аналогичный анализ, если предварительно принять:

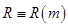 - номинальная ставка начисления процентов за один период владения в предположении, что ;

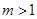R/m - ставка начисления процентов за один период выплат купонного дохода;

q/m - ставка купонного дохода за один период выплат.

По аналогии с предыдущим случаем можно получить следующую формулу для текущей стоимости облигации:

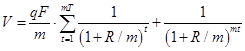(8)

Данная формула аналогичным образом может быть приведена к виду (6).

Анализ бессрочных облигаций

Применим описанный метод для анализа бессрочных облигаций.

Предположим, что 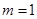 и 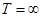, т.е. период выплат купонного дохода совпадает с периодом владения облигацией, а ее погашение не ожидается в обозримом будущем. При  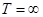текущей стоимостью финальной выплаты в формуле (2) можно пренебречь, поскольку по свойству предела

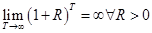(9)

что влечет 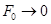 при 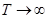. Таким образом, для бессрочной облигации

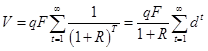(10)

Так как 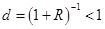, то по свойству суммы бесконечной геометрической прогрессии имеем

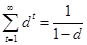(11)

На основании (11) из (10) следует:

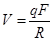(12)

Из (12) следует, что текущая стоимость облигации прямо пропорциональна величине выплачиваемого по ней купонного дохода и обратно пропорциональна ожидаемой доходности вложений.

Если Р - рыночная цена покупки облигации, то с учетом (12) ставка R* внутренней доходности облигации, определяемая из условия NPV= V-P=0, равна:

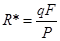(13)

Обычно ставка доходности, определяемая как отношение купонного дохода к рыночной цене (цене покупки) облигации, называется текущей доходностью (current yield) облигации. Таким образом, в случае бессрочных облигаций полная доходность, определяемая ставкой R*, совпадает с текущей доходностью облигации.