Произведем расчет вала шнека волчка на прочность и плотность.
Передаваемый момент
Mz = N/w, (4.78)
где N = 7×103 - передаваемая мощность, Вт;
w = 15,7 - угловая скорость вала, рад/с
Mz = 7×103/15,7 = 445×103 Н×мм.
Окружное усилие в зацеплении
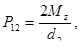 (4.79)
(4.79)
где d2 = 284 - диаметр делительной окружности зубчатого колеса, мм;
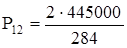 = 3133,8 Н.
= 3133,8 Н.
Осевое усилие в зацеплении
Q12 = P12×tgb, (4.80)
где b = 10 - угол наклона зубьев, град
Q12 = 3133,8×tg10 = 3133,8×0,176 = 551 Н.
Радиальное усилие в зацеплении
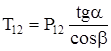 , (4.81)
, (4.81)
где a = 20 - угол зацепления в нормальном сечении, град,
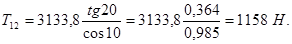
Определим реакции в вертикальной плоскости.
Сумма моментов относительно опоры В
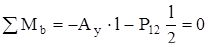 , (4.82)
, (4.82)
Из формулы (4.82) выразим реакцию Ах
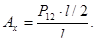 (4.83)
(4.83)
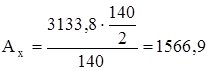 Н.
Н.
Сумма моментов относительно опоры А
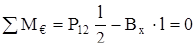 , (4.84)
, (4.84)
Из формулы (4.84) выразим опорную реакцию Вх
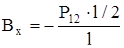 , (4.85)
, (4.85)
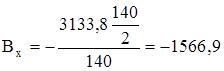 Н.
Н.
Определим изгибающие моменты в горизонтальной плоскости Муа = 0,
Му1 = Bx 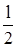 , (4.86)
, (4.86)
Му1=1566,9× 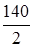 = 109,6×103 Н×мм.
= 109,6×103 Н×мм.
Определим суммарный изгибающий момент в наиболее нагруженном сечении В
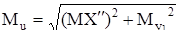 , (4.87)
, (4.87)
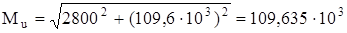 Н×мм.
Н×мм.
Эквивалентный момент по III гипотезе прочности
Мэкв = 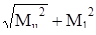 , (4.88)
, (4.88)
Мэкв = 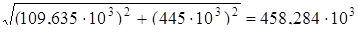 Н×мм.
Н×мм.
Определим диаметр вала под подшипником
Dn = 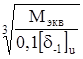 , (4.89)
, (4.89)
где [d -1] 4 = 50 – допускаемое напряжение изгиба, МПа
Dn =  = 61 мм.
= 61 мм.
Диаметр под подшипник принимаем из стандартного ряда Dn = 65 мм.
Определяем диаметр вала на выходном конце.
Dn = 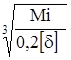 , (4.90)
, (4.90)
где [d] = 20 - допускаемое напряжение на чистое кручение, МПа;
Dn = 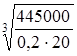 = 32 мм.
= 32 мм.
Принимаем диаметр выходного конца вала равным 35 мм
Выполним уточнённый расчёт вала, который заключается в определении коэффициентов запаса прочности в опасных сечениях. Материал вала круг, 100-е дм, Т 2590-88/30 дм, Т 1050-88 предел прочности для этого материала sB = 780 МПа, предел текучести sт = 440 МПа.
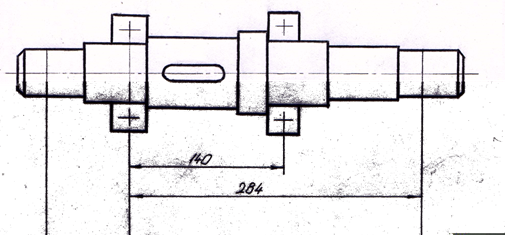

Рисунок 4.3 - Расчетная схема вала шнека.
Определяем предел выносливости при изгибе
s-1 = 0,43sВ , (4.91)
s-1 = 0,43×780 = 335 МПа.
Определяем предел выносливости при кручении
t-1 = 0,58s-1, (4.92)
t-1 = 0,58×335 = 193 МПа.
Концентрация напряжений обусловлена посадкой подшипника с гарантированным натягом.
Определяем амплитуду нормальных напряжений
sv= smax= 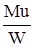 , (4.93)
, (4.93)
где W – осевой момент сопротивления, мм3;
W = 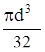 (4.94)
(4.94)
W = 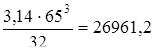 мм3;
мм3;
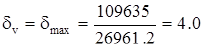 МПа.
МПа.
Определяем амплитуду и среднее напряжение цикла касательных напряжений
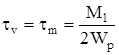 (4.95)
(4.95)
где Wр- полярный момент сопротивления, мм3;
Wр= 2×W, (4.96)
Wр= 2×26961,2 = 53922,4 мм3.
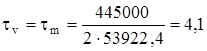 МПа.
МПа.
Определяем коэффициент запаса прочности по нормальным напряжениям
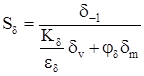 , (4.97)
, (4.97)
где Кd = 3,6 – эффективный коэффициент концентрации нормальных напряжений;
ed= 2,5 – масштабный фактор для вала диаметром 65 мм;
jd = 0,15 – коэффициент, учитывающий влияние постоянной составляющей цикла для сталей
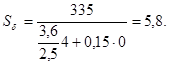
Определим коэффициент запаса прочности по касательным напряжениям
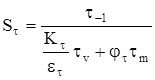 , (4.98)
, (4.98)
где Кt = 2,5– эффективный коэффициент концентрации касательных напряжений;
et = 0,68 – масштабный фактор для вала диаметром 65 мм;
jt = 0,1– коэффициент, учитывающий влияние постоянной составляющей цикла для сталей.
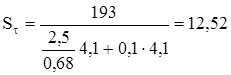 .
.
Определяем общий коэффициент запаса прочности
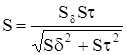 , (4.99)
, (4.99)
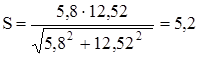 .
.
Условие прочности выполняется, если S ³ [ S ]. А так как
[ S ] = 2,5 - 4, то прочность и жесткость обеспечены.
Выполним проверку вала на сопротивление пластическим деформацием. Условие прочности
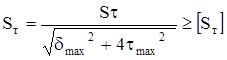 , (4.100)
, (4.100)
где Sт - коэффициент запаса по текучести,
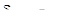 - наибольшие нормальные и касательные напряжение при передаче валом пикового момента, МПа;
- наибольшие нормальные и касательные напряжение при передаче валом пикового момента, МПа;
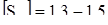 - требуемый коэффициент запаса прочности по текучести;
- требуемый коэффициент запаса прочности по текучести;
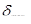 = 2×dv= 2×4 = 8 МПа.
= 2×dv= 2×4 = 8 МПа.
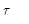 = 2×4,1 = 8,2 МПа.
= 2×4,1 = 8,2 МПа.
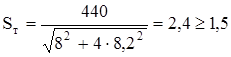 .
.
Этот коэффициент запаса достаточен.
Дата: 2019-05-28, просмотров: 444.