Пусть имеется выборка х=(х1,...,xn) размера n. Известно, что эта выборка принадлежит одному из двух распределений: W(x|A1) или W(x|A2). Априорные вероятности состояний А1 и А2 равны, соответственно, v1 и v2=1-v1. Необходимо найти оптимальный с точки зрения возможных потерь метод принятия решения о том, какому из указанных распределений принадлежит выборка.
Пусть H1 и H2 гипотезы о том, что выборка принадлежит распределениям, соответственно, W(x|A1) и W(x|A2), а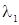 
и 
-решения, состоящие в принятии гипотез, соответственно, Н1 или Н2.
Определим граничное значение х*, в зависимости от которого по текущему х будем принимать решения в пользу гипотезы Н1 или Н2. При х<х*, условимся принимать решение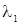 
, тогда, как при х>х*, будем принимать решение 
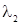. Вероятности неизбежных ошибок при принятии решения выражаются как:
|
|
где р1 - вероятность принятия решения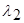 
при реализации гипотезы Н1;
р2 - вероятность принятия решения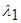 
при реализации гипотезы Н2.
Вероятности принятия правильных решений можно выразить как:
|
|
Пусть известны цены правильных и ошибочных решений, так что:
С11-цена правильного принятия решения 
;
С21-цена ошибочного принятия решения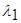 
;
С22-цена правильного принятия решения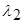 
;
С12-цена ошибочного принятия решения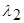 
;
С12>C11, C21>C22.
Среднее значение потерь равно:
|
R=v1r1+v2r2
|
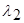|A1)+C12P( |A1)=C11(1-p1)+C12p1
|
r2=C21P(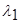 
|A2)+C22P( 
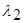|A2)=C21p2+C22(1-p2)
Подставляя в (29) выражения (30) и (31), получим:
|
Подставляя величины р1 и р2 из (25) и (26) в промежуточное выражение (32), находим, что окончательно среднее значение потерь определяется как:
|
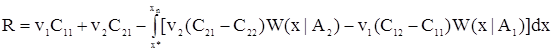
Минимальное значение средних потерь R достигается, когда подынтегральная функция будет неотрицательной, или когда при интегрировании в области [x*,xn]:
|
v2(C21-C22)W(x|A2)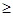 
v1(C12-C11)W(x|A1)
Граничное значение х* находится из выражения:
|
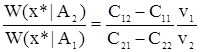
Функция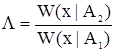 
называется отношением правдоподобия.
Обычно вместо граничного значения х* используется пороговое значение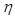 
, так что:
|
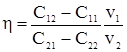
Тогда оптимальный метод принятия решения можно выразить так:
при L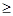 
, принимается решение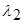 
; при L< 
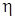, принимается решение .
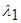Отношения правдоподобия есть, по сути, отношение вероятностей наступления состояний А2 и А1 в зависимости от значения х:
|
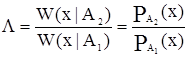
С учетом вышеописанного, рассмотрим нахождение порога принятия решения для прогнозирования и принятия соответствующего рыночной ситуации правильного решения.
Пусть необходимо совершить определенную сделку покупки или продажи ценной бумаги. Такая ситуация может быть обусловлена приказом клиента, распоряжением руководства фирмы или просто собственным решением трейдера, принятым в результате рыночного анализа. Допустим, необходимо купить пакет акций.
Автор диссертации /1/ рассматривает два варианта вычисления порога принятия решения в зависимости от игнорирования или учета величины потенциальной потери.
Рассмотрим первый вариант, когда величина потенциальной потери не принимается в расчет. В этом конкретном случае переменные, входящие в выражение (36), определяются следующим образом.
Величины v2 и v1 описывают вероятности, соответственно, повышения и понижения котировок, которые показывают, как часто встречаются эти события в реальных условиях. Пусть частоты появления этих двух событий одинаковы, тогда:
|
v1=v2=0,5
Величина С11 представляет собой стоимость правильного решения «не покупать» при последующем снижении котировок. В рассматриваемом варианте:
|
С11=0
при этом отсутствуют как потери, так и выигрыши.
Величина С12 описывает стоимость ошибочного решения «покупать», при последующем снижении котировок. Эта стоимость складывается из величины убытка L, обусловленного снижением котировочных цен на купленные акции, и уплаченной комиссии за совершение сделки q:
|
С12=L+q
L вычисляется как произведение величины изменения САЛК и количества купленных акций :
|
|
S(i+1)<>S(i)
В данной работе принимается, что величина ближайшего изменения САЛК |S(i+1)-S(i)| равняется текущей разнице между ценами лучших предложений на покупку и продажу.
Величина C21 представляет собой стоимость ошибочного решения «не покупать» при дальнейшем увеличении котировок. В данном случае теряется потенциальная прибыль, величина которой равна:
С21=L-q
(43)
Величина C22 выражает стоимость правильного решения «покупать» при дальнейшем увеличении котировок, равную полученной прибыли:
|
С22=-(L-q)
Подставив величины С11, С12, С21, С22, определенные выражениями (38), (39), (40), (41), (44) в формулу (36), получим:
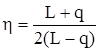
Из выражения (45) видно, что если величина q сравнима с L, потенциальная прибыль, в основном, пойдет на компенсацию комиссионных. В таких случаях, в соответствии с вышеизложенным методом оптимального принятия решения, следует покупать только при значениях Рр(a,b,c), близких к 1.
В случае, когда прибыль много больше комиссии (L>>q), из выражения (45) следует, что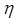 
~0,5. Это означает, что осуществлять покупку следует, если:
|
Рр(a,b,c)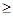 
0,5Pn(a,b,c)
Во втором варианте вычисления порога принятия решения учитывается величина потенциальной потери. В этом случае в выражении (36) переменная С11 определяется, исходя из следующих соображений. При правильном решении не покупать, с учетом последующего понижения котировок, трейдер виртуально выигрывает величину L+q. Так что:
|
С11=-(L+q)
После подстановки (38), (40), (43), (44), (47) в выражение (36), последнее приобретает следующий вид:
|
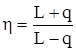
При условии L>>q, решение о покупке можно принимать только когда Рр(a,b,c) 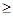Pn(a,b,c).
Дата: 2019-05-28, просмотров: 189.
