Рассмотрим схему образования законченного ИПС из незаконченного. Ввиду большого числа возможных вариантов трансформаций незаконченного ИПС в различные ИПС в случаях большого размера последних, ограничимся рассмотрением формирования ИПС, размер которых не превышает 3 сделки. Схема образования различных ИПС размером в 3 сделки показана на рис. 4.
Схема формирования различных ИПС размером в 3 сделки
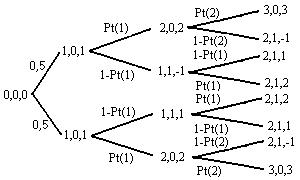
Рис. 4
Линиями с наклоном вверх, обозначены сделки, совершаемые в направлении аккумулирования. Линии с наклоном вниз обозначают сделки, совершенные в направлении диссипации. Возле каждой линии указаны вероятности совершения соответствующей ей сделки.
Зная вероятности Ррac(a,b,c) и Рnac(a,b,c) изменения САЛК по завершению ИПС определенного размера, рассмотрим случай, когда размер ИПС неизвестен, что соответствует реальным условиям торгов.
Из экспериментальных данных следует, что частота появления ИПС определенного размера l=а+b уменьшается с увеличением значения l (табл. 2).
Таблица 2
Количество ИПС размера l=а+b в экспериментальной статистической базе данных
| l | N(l) |
| 1 | 182 |
| 2 | 117 |
| 3 | 86 |
| 4 | 67 |
| 5 | 44 |
| 6 | 38 |
| 7 | 25 |
| 8 | 18 |
| 9 | 12 |
| 10 | 13 |
| 11 | 4 |
| 12 | 4 |
| 13 | 7 |
N(l)-количество ИПС размера l в экспериментальной статистической базе данных.
Общее количество ИПС в экспериментальной статистической базе данных – n=627.
Делением каждой величины N(l) на n были получены экспериментальные значения вероятностей f*(l) появления ИПС с размером l. Значения функции f*(l) приведены в табл. 3.
Таблица 3
Экспериментальные значения вероятностей f*(l)появления ИПС с размером l
| l | f*(l) |
| 1 | 0,290 |
| 2 | 0,187 |
| 3 | 0,137 |
| 4 | 0,107 |
| 5 | 0,070 |
| 6 | 0,061 |
| 7 | 0,040 |
| 8 | 0,029 |
| 9 | 0,019 |
| 10 | 0,021 |
| 11 | 0,006 |
| 12 | 0,006 |
| 13 | 0,011 |
|
 .
.
Согласно правилу В.И. Романовского, гипотезу о данном виде функции f(l) можно считать верной, если число R<3:
|
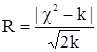 ,
,
где 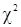 – статистика Пирсона;
– статистика Пирсона;
k – число степеней свободы.
Величина  вычисляется по формуле:
вычисляется по формуле:
|
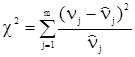 ,
,
где 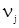 – абсолютные экспериментальные частоты:
– абсолютные экспериментальные частоты: 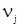 =N(j);
=N(j);
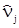 – абсолютные теоретические частоты;
– абсолютные теоретические частоты;
m – минимальная величина размера ИПС до которой происходит подсчет  .
.
При этом m и 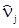 вычисляются по формулам:
вычисляются по формулам:
|
m 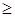 1+ln n
1+ln n
|
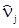 =f(j)n
=f(j)n
|
k=m-2
Было выбрано m=8, при этом число R, вычисленное по формулам (13)-(17) составило 0,95<3, т.е. гипотезу о данном виде функции (12) можно считать верной.
Значения f(l), в зависимости от величины l, приведены в табл. 4.
Таблица 4
Значения аппроксимированной зависимости f(l)вероятности появления ИПС размером l от величины l
| l | f(l) |
| 1 | 2 |
| 1 | 0,262 |
| 2 | 0,192 |
Продолжение табл. 4
| 1 | 2 |
| 3 | 0,140 |
| 4 | 0,103 |
| 5 | 0,075 |
| 6 | 0,055 |
| 7 | 0,040 |
| 8 | 0,029 |
| 9 | 0,021 |
| 10 | 0,016 |
| 11 | 0,011 |
| 12 | 0,008 |
| 13 | 0,006 |
Пусть lmax-размер ИПС, начиная с которого, вероятность появления ИПС с размерами l 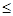 lmax по статистике меньше 0,01. Из приведенных в табл.4.12 результатов видно, что lmax =12 для исследуемых акций. В дальнейших расчетах, будем считать, что максимальный размер ИПС не превышает величины lmax. С учетом этого каждому незаконченному ИПС, размера l (l
lmax по статистике меньше 0,01. Из приведенных в табл.4.12 результатов видно, что lmax =12 для исследуемых акций. В дальнейших расчетах, будем считать, что максимальный размер ИПС не превышает величины lmax. С учетом этого каждому незаконченному ИПС, размера l (l 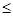 lmax) можно поставить в соответствие функцию fl(х), которая определяет вероятности появления законченных ИПС с размером х: l
lmax) можно поставить в соответствие функцию fl(х), которая определяет вероятности появления законченных ИПС с размером х: l 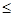 х
х 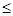 12. Функции fl(х) выражаются как:
12. Функции fl(х) выражаются как:
|
 ,
,
где 1 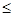 l
l 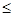 lmax, l
lmax, l 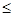 x
x 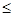 lmax.
lmax.
Искомые величины Рр(a,b,c) и Рn(a,b,c) рассчитываются следующим образом:
|
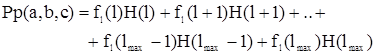
|
где l - размер текущего незаконченного ИПС, l=a+b;
fl(x) - вероятность того, что ИПС размером x будет законченным;
H(x) - вероятность того, что новая сделка вызовет повышение САЛК
законченного ИПС размером x.
Поскольку с увеличением значения x число слагаемых в функции H(х) увеличивается по закону геометрической прогрессии, формулы расчета значений H(х) приведены только для H(l) и H(l+1), так что:
если с>0:
|
H(l)=Рpаc(a,b,c)
|
H(l+1)=Pt(c)Рpаc(a+1,b,c+1)+(1-Pt(c))Рpаc(a,b+1,-1)
|
H(l)=Рpаc(a,b,c)
|
H(l+1)=(1-Pt(c))Рpаc(a+1,b,1)+Pt(c)Рpаc(a,b+1,c-1)
где Рpаc(a,b,c) - вероятность повышения САЛК законченного ИПС с параметрами a,b,c;
Pt(c) - вероятность совершения новой сделки по направлению хвоста индекса незаконченного ИПС в зависимости от величины с.
Дата: 2019-05-28, просмотров: 289.