ИСПОЛЬЗОВАНИЕ ИЗМЕРЕНИЙ И РЕШЕНИЕ ЗАДАЧ НА МЕСТНОСТИ ПРИ ИЗУЧЕНИИ НЕКОТОРЫХ ТЕМ ШКОЛЬНОГО КУРСА ГЕОМЕТРИИ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ДИПЛОМНАЯ РАБОТА

ИСПОЛЬЗОВАНИЕ ИЗМЕРЕНИЙ И РЕШЕНИЕ ЗАДАЧ НА МЕСТНОСТИ ПРИ ИЗУЧЕНИИ НЕКОТОРЫХ ТЕМ ШКОЛЬНОГО КУРСА ГЕОМЕТРИИ

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ . . . . . . . . . . 3

ГЛАВА 1. Содержание и методические особенности проведения факультатива

§1. Простейшая геометрия на местности . . . . . 5

§2. Измерения при различных ограничениях . . . 11

§3. Преподавание математики в сельской школе. . . 12

§4. Факультатив, как одна из форм проведения внеклассной

работы по геометрии . . . . . . . 15

§5. Методика проведения факультативных занятий по теме «Решение

задач на местности» . . . . . . . 16

§6. Педагогический эксперимент . . . . . 30

ГЛАВА 2. Комплекс задач, решаемых на местности

§1. Задачи с измерениями при различных ограничениях . 33

§2. На равном расстоянии . . . . . . 39

§3. Задачи, предлагаемые учащимся сельской школы . 47

ЗАКЛЮЧЕНИЕ . . . . . . . . . 62

ЛИТЕРАТУРА . . . . . . . . . 64

Введение

Пусть читатель прогуливается в огромном

саду геометрии, в котором он сможет подобрать

себе такой букет, какой ему нравится.

Давид Гильберт.

Одной из самых важных проблем сегодня в нашей стране является проблема образования. Причем речь идет не о высшей ступени, а о средней, самой главной, ступени образования. Сущность проблемы заключается в том, что у учащихся снизился интерес к изучению, как всех предметов, так и математики, в частности. Поэтому цель работы состоит в повышении интереса к математике за счет изучения нового, не связанного с общеобразовательной программой материала.

В наше время происходят процессы глобализации образования, широкого внедрения новых технологий дистанционного обучения, Интернет и мультимедиа-технологий. Необходимо видеть, что наряду с несомненными достоинствами происходящие процессы несут в себе и отрицательные моменты. Технологизация, компьютеризация образования удаляет ученика от учителя других учеников. Одним из возможных направлений сближения может быть повышение интереса к предмету, демонстрация его практических приложений, возможность решать интересные и практически значимые задачи вместе (как с учителем, так и с группой учеников). Особенностью большинства задач на местности является то, что для получения данных задачи и ее решения необходимо участие нескольких человек.

Образование теснейшим образом связано с духовной культурой. Цель всего образования и математического образования в частности – формирование, воспитание духовной культуры личности. Геометрическое мышление в своей основе является разновидностью образного, чувственного мышления.

Наглядность и практичность обучения геометрии являются необходимыми условиями успешного ее изучения. Формирование отвлеченного мышления у школьников с первых школьных шагов требует предварительного пополнения их сознания конкретными представлениями. При этом удачное и умелое применение наглядности побуждает учеников к познавательной самостоятельности и повышает их интерес к предмету, является важнейшим условием успеха [7].

Наглядные методы применяются на всех этапах педагогического процесса. Формирование геометрических представлений является важным разделом умственного воспитания, политехнического образования, имеют широкое значение во всей познавательной деятельности человека [13] .

Известно, что механическое, нетворческое усвоение школьниками большого объема фактов, представленных в школьном курсе математики, несовместимо с подлинной образованностью, с полноценным воспитанием умственных, нравственных и других качеств личности учащихся, подготовкой их к активному участию в создании материальных и духовных ценностей независимо от того, какую профессию они получат в дальнейшем. Удачный подбор содержательных практических задач еще не обеспечивает должного эффекта. Такие задачи, как правило, вызывают у учащихся затруднения. Условия прикладной задачи только тогда легко доходит до сознания учащихся, когда они (а тем более учитель) встречались с описываемой производственной ситуацией в реальной действительности. Поэтому при постановке задач следует широко опираться на наглядные аналоги из производственного окружения школы, на трудовой опыт учащихся.

Велико значение геометрии в развитии личности. Установлено, что развитое пространственное мышление, прочные математические знания и умения школьников представляют собой важнейшие компоненты готовности к непрерывному образованию, что является актуальным в настоящее время. Необходимость достаточно высокого уровня развития пространственного мышления для успешного усвоения учащимися общеобразовательных предметов и дальнейшего профессионального образования в условиях современного производства доказана многими исследователями психологами.

Умение решать задачи на местности – так же как и руководить их решением – приходит с опытом, при систематическом использовании таких задач в учебном процессе.

Все выше сказанной говорит об актуальности проблемы исследования, которая заключается в изучении теории и отборе содержания данной темы для школьного курса математики.

Объектом исследования является процесс обучения учащихся математике.

Предметом исследования – содержание темы «Использование измерений и решение задач на местности при изучении школьного курса геометрии» и организация деятельности учителя и учащихся.

Задачи исследования:

1. Изучить математическую, психолого-педагогическую, методическую литературу по проблеме исследования.

2. Подобрать и адаптировать для школьников теоретический и практический материал, позволяющий продемонстрировать приложение геометрических фактов к решению задач на местности.

3. Найти эффективные пути и способы организации факультативных занятий.

4. Разработать методику проведения факультативных занятий по теме «Решение задач на местности».

5. Провести экспериментальную проверку отобранного материала и методики факультативных занятий.

ГЛАВА 1

Педагогический эксперимент

По проблеме исследования был проведен естественно – педагогический эксперимент.

Эксперимент проходил в три этапа:

1 этап – констатирующий эксперимент. При его проведении были выявлены знания учащихся по теме «Использование и измерений и решение задач на местности при изучении некоторых тем школьного курса геометрии», при этом использовались различные формы и методы выявления знаний, такие как: анкетирование, беседы с учащимися и учителями, наблюдение за учащимися.

2 этап – поисковый. На этом этапе производился отбор заданий для проведения факультатива. В результате был подобран комплекс заданий, при работе с которым учащиеся знакомятся с задачами, решаемыми на местности, осуществляется повторение и систематизация знаний школьного курса геометрии, пропедевтика ряда геометрических понятий, повышается интерес школьников к математике, вырабатывается осознанный подход к применению знаний на практике.

3 этап – обучающий (формирующий), когда была проведена экспериментальная проверка знаний, полученных в ходе проведения факультативных занятий, в виде опроса.

На третьем этапе эксперимента проводилась проверка гипотезы.

Выводы: факультативные занятия способствуют углублению и расширению знаний, развитию интереса учащихся к предмету, развитию математических способностей, привитию школьникам интереса и вкуса к самостоятельным занятиям, воспитанию и развитию инициативы и творчества, развитию определенных сторон мышления и черт характера учащихся. Также занятия содействуют профессиональной ориентации учащихся. На факультативах осуществляется подготовка к выпускным экзаменам за счет повторения теории и решения различных задач. У учащихся в процессе изучения темы повысился интерес к геометрии, чего не наблюдается в классах, где факультативные занятия не проводились.

Таким образом, эксперимент подтвердил выдвинутую гипотезу: если систематически и целенаправленно включать в школьный курс геометрии разнообразный материал, то это повысит интерес учащихся к геометрии и разовьет их творческие способности.

ГЛАВА 2

Существует множество различных способов производить измерения при помощи незамысловатых приборов и даже без всяких приспособлений.

Самый легкий и самый древний способ – без сомнения, тот, который греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды [10]. Он воспользовался ее тенью. Фалес, – говорит предание, - избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна также равняться длине отбрасываемой ею тени. Конечно, длину тени надо было считать от средней точки квадратного основания пирамиды; ширину этого основания Фалес мог измерить непосредственно.

Фалес жил задолго до Евклида, автора замечательной книги, по которой обучались геометрии в течение двух тысячелетий после его смерти. Заключенные в ней истины не были открыты в эпоху Фалеса. А чтобы воспользоваться тенью для решения задачи о высоте пирамиды, надо было знать уже некоторые геометрические свойства треугольника, - именно следующие два:

1) что углы при основании равнобедренного треугольника равны, и обратно - что стороны, лежащие против равных углов треугольника, равны между собою;

2) что сумма углов всякого треугольника (или по крайней мере прямоугольного) равна двум прямым углам.

Только вооруженный этим знанием Фалес вправе был заключить, что, когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и, следовательно, вершина пирамиды, середина ее основания и конец ее тени должны обозначать равнобедренный треугольник. Однако способ Фалеса в указанном виде применим не всегда.

На равном расстоянии

В настоящем параграфе рассматривается несколько практических задач, в которых нужно использовать геометрический материал для нахождения точек или линий на местности из соображений равенства каких-либо расстояний. Построения, которые понадобятся для решения этих задач, должны быть по возможности более простыми. Если они не потребуют никаких средств, выходящих за рамки простейшей геометрии на местности, то такие построения можно будет осуществить в обычных условиях без использования сколько-нибудь сложных измерительных приборов [2]. В противном случае для реализации построений можно изобразить исходную конфигурацию на плане и, решив задачу на бумаге с помощью циркуля и линейки, перенести результат на местность.

Ниже предполагается, что все населенные пункты имеют незначительные размеры и могут быть приняты в задачах за точки, а магистрали, каналы и железные дороги являются прямыми и имеют пренебрежимо малую ширину, т.е. могут быть представлены как прямые линии.

Задачи

2.1. Невдалеке от двух населенных пунктов проходит шоссе. В каком месте этого шоссе нужно построить автозаправочную станцию, чтобы расстояния от нее до обоих пунктов были одинаковыми?

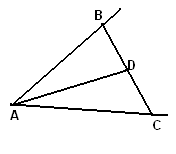
Обозначим через А и В данные в задаче населенные пункты и проведем на местности серединный перпендикуляр к отрезку АВ. Так как все точки этого перпендикуляра равноудалены от пунктов А и В и никакие другие точки этим свойством не обладают, то автозаправочную станцию нужно построить в точке пересечения перпендикуляра с шоссе (если такая точка найдется).

2.2. Жильцы трех домов решили совместными усилиями построить колодец. Какое место для колодца следует выбрать, чтобы все три расстояния от него до домов были одинаковыми?

Пусть А, В и С — точки расположения трех данных домов. Проведем серединные перпендикуляры к отрезкам АВ и ВС. Тогда точка О их пересечения будет единственной точкой, равноудаленной от точек А, В и С, поскольку для этой точки выполнены равенства АО=ОВ и ВО=ОС, а если точку О выбрать иначе, то для нее хотя бы одно из указанных равенств будет несправедливо. Заметим, что проведенные перпендикуляры могут и не пересечься, но только в случае, когда точки А, В и С лежат на одной прямой. Таким образом, искомое место для колодца — точку О — можно найти приведенным способом, но лишь при условии, что дома расположены не на одной прямой.

2.3. Две магистрали пересекаются под углом, внутри которого протекает речка. Где построить мост через речку, чтобы расстояния от него до обеих магистралей были одинаковыми?

Проведем биссектрису угла, образованного магистралями. Так как все точки этой биссектрисы равноудалены от магистралей и никакие другие точки внутри угла этим свойствам не обладают, то мост через речку нужно построить в точке пересечения биссектрисы с речкой (если такая точка найдется).

2.4. Две магистрали пересекают канал в разных местах. Где нужно разместить пионерский лагерь, чтобы расстояния от него до канала и до каждой магистрали оказались одинаковыми? Укажите место расположения пионерского лагеря, при котором эти расстояния минимальны?

Каждая магистраль, пересекаясь с каналом, образует две пары вертикальных углов, а четыре их биссектрисы составляют две прямые (рис. 29). Так как все точки этих биссектрис равноудалены от канала и соответствующей магистрали, а никакие другие точки этим свойством не обладают, то все возможные места расположения пионерского лагеря, лежат на пересечениях биссектрис углов при разных вершинах А и В.

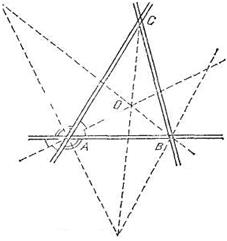
Рис. 29

Таких точек пересечения может быть, вообще говоря, четыре, поскольку любая из двух прямых, проходящих через вершину А, может пересечься с любой из двух прямых, проходящих через вершину В. Если магистрали не параллельны, то никакие пары этих прямых не параллельны и все четыре точки пересечения реализуются, а наименьшее расстояние до канала (а значит, и до магистралей) достигается в той точке О пересечения биссектрис, которая лежит внутри треугольника, образованного каналом и магистралями. Действительно, из двух точек пересечения биссектрисы внутреннего угла треугольника при вершине А с биссектрисами углов при вершине В ближе к вершине А (а значит, и к каналу) лежит точка О. Аналогично из двух точек пересечения, лежащих на биссектрисе внутреннего угла треугольника при вершине В, также выбираем точку О. Наконец, последняя точка пересечения биссектрис внешних углов треугольника при вершинах А и В лежит вместе с точкой О на биссектрисе угла треугольника при вершине С, причем точка О лежит ближе к вершине С, следовательно, ближе к магистралям и, стало быть, к каналу. Если же магистрали параллельны, то четыре биссектрисы углов при вершинах А и В образуют параллелограмм (из-за симметрии всей картины относительно середины отрезка АВ), поэтому обе точки пересечения этих прямых равноудалены от канала.

2.5. В каком направлении через город должна проходить магистраль, чтобы два данных населенных пункта лежали по разные стороны от нее на одинаковом расстоянии?

Пусть через город А нужно провести магистраль, равноудаленную от пунктов В и С (рис. 30). Так как точки В и С должны лежать по разные стороны от искомой магистрали, то она должна пересечь отрезок ВС, причем точка пересечения должна совпадать с серединой этого отрезка (что вытекает из равенства соответствующих прямоугольных треугольников). Таким образом, искомая магистраль определена однозначно, если только сама точка А не совпадает с серединой отрезка ВС (в случае их совпадения годится любое направление).

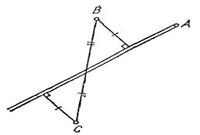
Рис. 30

2.6. Как должна проходить магистраль, чтобы расстояния от нее до трех данных населенных пунктов были одинаковыми? Укажите положение магистрали, при котором эти расстояния минимальны.

Обозначим через А, В и С три данных населенных пункта. Если искомая магистраль может проходить так, чтобы все три точки лежали по одну сторону относительно магистрали (в том числе и на ней самой) и к тому же на равном расстоянии от нее, то точки А, В и С лежат на одной

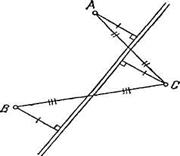
Рис. 31

прямой, параллельной магистрали. В этом случае расстояние минимально, когда магистраль проходит через эти точки.

В противном случае две из данных точек, скажем А и В, должны лежать по одну сторону от искомой магистрали, а третья — по другую (рис. 31). Так как магистраль равноудалена от точек А и С, то она проходит через середину отрезка АС (см. решение задачи 2.5), а так как она равноудалена от точек В и С, то проходит и через середину отрезка ВС. Таким образом, мы доказали, что искомая магистраль проходит по одной из трех средних линий треугольника ABC .

Среди возможных расположений магистрали наименьшее расстояние до точек А, В и С, равное половине наименьшей высоты треугольника ABC , достигается, когда магистраль параллельна наибольшей стороне этого треугольника (точнее, какой-нибудь из наибольших сторон, если их несколько), поскольку наименьшая высота в треугольнике соответствует наибольшей стороне — ведь их произведение есть константа, равная удвоенной площади треугольника.

2.7. Магистраль пересекает канал под углом, внутри которого расположен населенный пункт. В каком направлении следует провести через этот пункт прямую дорогу, чтобы расстояния по ней до магистрали и до канала оказались одинаковыми?

Проведем прямую через точку А пересечения магистрали с каналом и через данный населенный пункт В. Рассмотрим точку С па этой прямой, удаленную от точки В на расстояние АВ (рис. 32). Тогда если искомая дорога пересекает магистраль и канал в точках D и Е соответственно, то точка Весть центр симметрии четырехугольника ADCE, который, стало быть является параллелограммом. Теперь сами точки D и Е можно найти, проведя через точку С прямые, параллельные каналу и магистрали, до пересечения их соответственно с магистралью (в точке D) и с каналом (в точке Е).

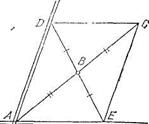
Рис. 32

2.8. Железная дорога пересекает канал под острым углом, внутри которого расположен населенный пункт. В каком месте железной дороги нужно расположить полустанок, чтобы расстояния от него до этого пункта и до канала оказались одинаковыми? Укажите положение полустанка, при котором эти расстояния минимальны.

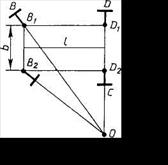
Из точки А пересечения железной дороги с каналом через данный населенный пункт В проведем луч. Опустим из какой-либо точки О железной дороги перпендикуляр ОС к каналу и найдем на луче АВ точки, удаленные

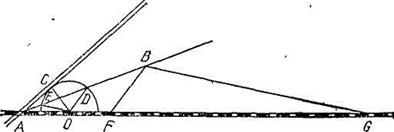
Рис. 33

от точки О на расстояние ОС. Таких точек окажется две — это буду точки D и Е, лежащие на окружности с центром О и радиусом ОС. Для определенности будем считать, что DA > EA (рис. 33). Проведем отрезки BF и BG , соединяющие точку В с точками F и G на железной дороге и параллельные отрезкам DO и ЕО соответственно. Тогда из подобия соответствующих треугольников будет следовать, что точки F и G равноудалены от канала и от точки В, т. е. они укажут искомые места расположения полустанка. Никаких других возможностей для расположения полустанка нет, поскольку для любой искомой точки существует преобразование гомотетии относительно точки А, переводящее искомую точку в точку О, а точку В в точку луча АВ, удаленную от точки О на расстояние ОС, т. е. в одну из точек D или Е.

Минимальное расстояние до полустанка достигается в точке F , для которой имеем

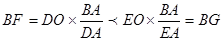ибо 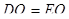и .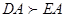

2.9. Две магистрали пересекаются под углом, внутри которого расположен населенный пункт. Как выбрать место для устройства пруда круглой формы, чтобы расстояния от него до этого пункта и до каждой магистрали оказались одинаковыми?

Найдем точку О, в которой должен находиться центр пруда. Поскольку точка О равноудалена от двух данных магистралей, то она лежит на биссектрисе угла между ними. Таким образом, задача сводится к нахождению на данной прямой l – биссектрисе - точки О , равноудаленной от данной точки А – населенного пункта – и от другой данной прямой – той из магистралей, которая образует с прямой l угол, содержащей точку А (этот угол будет обязательно острым, так как он равен половине угла между магистралями). Такая ситуация разобрана в решении задачи 2.8.

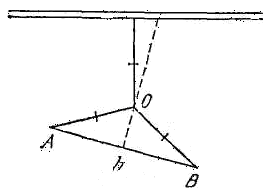
Рис. 34

2.10. Как выбрать место для устройства пруда круглой формы, чтобы расстояния от него до данной магистрали и до каждого из двух данных населенных пунктов, расположенных с одной стороны от магистрали, были одинаковыми?

Найдем точку О, в которой должен находиться центр пруда. Поскольку точку О равноудалена от двух данных населенных пунктов А и В, то она лежит на серединном перпендикуляре к отрезку АВ (рис. 34). Таким образом, задача сводится к нахождению на данной прямой h (перпендикуляре) точки О, равноудаленной от точки А или точки В и от другой данной прямой l (магистрали). Если прямые h и l не параллельны и не перпендикулярны, то они в пересечении образуют острый угол, внутри которого расположена одна из точек А и В (ведь обе эти точки лежат по одну сторону от прямой l). Способ нахождения точки О в этом случае указан в решении задачи 2.8. Если прямые h и l перпендикулярны, то точка О должна быть равноудалена от точки их пересечения и от точки А, и этот случай также был разобран в решении задачи 2.1. Наконец, если прямые h и l параллельны, то точка 0 должна быть удалена от точки А на расстояние, равное расстоянию d между прямыми h и l. Поэтому искомая точка лежит на пересечении прямой h и окружности с центром А и радиусом d (таких точек пересечения будет две, поскольку расстояние от точки А до прямой h меньше d — ведь одна из точек А или В расположена между прямыми h и l).

ОКРУЖНОСТЬ

3.1. Для возможности поворота автомобиля (или колесного трактора) направляющие (передние) колеса соединены с осью шарнирам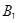и и 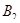так, что плоскости колес (рис. 35) могут поворачиваться относительно оси. Во время правильного поворота все четыре колеса катятся по дугам концентрических окружностей, причем проекции колес являются касательными к этим окружностям [19]. Докажите, что правильный поворот возможен лишь тогда, когда направляющие колеса поворачиваются на разные углы.

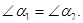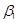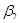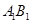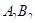Решение. Допустим противное, что Тогда равны и вертикальные им углы и , а значит, по признаку параллельности прямые и параллельны.

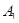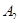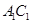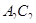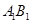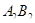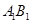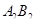С другой стороны, поскольку углы и прямые, а прямые и — касательные к окружности качения, то прямые и содержат радиусы концентрических окружностей. Значит, прямые и пересекаются. Противоречие.

Замечание. Рассмотренный эффект на практике достигается с помощью так называемой рулевой трапеции.

ТЕОРЕМА ПИФАГОРА

3.2. Телевизионные радиосигналы распространяются на 15% дальше пределов прямой видимости антенны. При каком наибольшем расстоянии s от передающей антенны высоты Н можно принять телепередачу с помощью приемной антенны высоты h ? Определить, при каком максимальном расстоянии можно принять передачу с помощью антенны высотой 20м с Останкинской телебашни (ее высота 538м).

Решение. Вершина В принимающей антенны (рис. 36) за счет шаровой поверхности Земли будет в крайнем случае еще видна из вершины передающей антенны А тогда, когда точки А и В лежат на касательной к земной поверхности. В этом случае 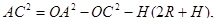где R – радиус Земли. Так как Н очень мало по сравнению с 2 R, то 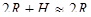, а потому 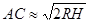. Полагая в этой формуле 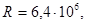получаем .

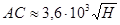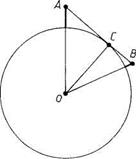
Рис. 36

Определив таким же образом ВС, найдем АВ. Увеличив полученную величину на 15%, получаем искомую формулу для s (в м): s 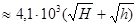. Из нее теперь нетрудно получить ответ и на второй вопрос задачи.

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

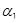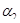3.3. Докажите, что правильный поворот (см. 3.1.) автомобиля возможен лишь тогда, когда направляющие колеса поворачиваются на такие углы и , что 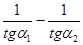есть величина постоянная при любых возможных 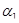и .

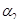Решение. В силу условия правильного поворота точка О (рис. 37) должна лежать на продолжении задней оси CD . Так как 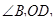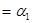, , 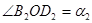то из прямоугольных треугольников 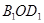и 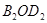находим:

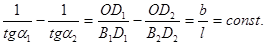
3.4. Величина угла на местности часто определяется линейными промерами. На сторонах угла откладывают отрезки (рис. 38) АВ = АС = 10 м и измеряют ВС. Какова величина угла, если ВС = 12 м?

Решение. Пусть D — середина ВС. Тогда AD — высота биссектриса

Рис. 37 Рис. 38

равнобедренного треугольника. Из прямоугольного треугольника ADB имеем:

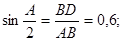
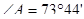3.5. В строительной практике широко распространены понятия уклона и угла наклона (участка дороги, откоса плотины, стенок канала, скатов крыши и т. п.). Пусть ЕС— некоторый отрезок на местности, CD — вертикальная, ED — горизонтальная прямая. Углом наклона СЕ называется угол CED ; уклоном отрезка СЕ называется отношение его подъема CD к его горизонтальной проекции ED . Какая зависимость существует между углом наклона ее отрезка ЕС и его уклоном k ?

Ответ., k = tg .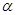

ПОДОБИЕ ФИГУР

3.8. На рисунке 41 изображен высотомер лесника. Он представляет собой прямоугольную пластинку размером 10Х 10 см с закрепленным в точке А отвесом, шкалой на стороне ВС и визирами в точках А и D . Наведя с помощью визиров сторону AD на вершину дерева Е и заметив деление шкалы, которое показывает отвес AF , лесник с помощью несложной формулы и находит высоту дерева. Пусть, например, BF = 3 см. Докажите, что

(*)

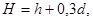где Н — высота дерева, h — высота человека на уровне глаз, d — расстояние от дерева до человека (все размеры в метрах).

Рис. 41

Решение. Так как 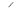GEA = 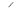AFB (докажите это, рассматривая пары параллельных прямых), то прямоугольные треугольники EGA и FBA подобны. Поэтому (все размеры в см):

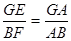или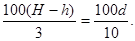

Отсюда и следует (*).

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ

3.9. Высевающий аппарат большинства сеялок представляет собой цилиндрическую катушку с желобками (рис. 42), которые при вращении катушки захватывают зерна и высыпают из сеялки. При проектировании катушки вначале определяют число желобков п и ширину желобка t , исходя из размеров и механических свойств зерен, для которых предназначена сеялка. Эти данные позволяют найти диаметр катушки.

Каким должен быть диаметр катушки высевающего аппарата зерновой сеялки у которой t =13.6 мм (с учетом ширины ребра между смежными желобками), п=12?

Рис. 42

Решение. Требуется найти диаметр окружности, описанной около правильного n-угольника со стороной а_п — t . По известной формуле получаем:

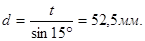
Площади фигур

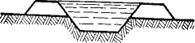
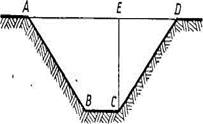
3.12. Требуется выкопать канал для подачи воды к рыбоводному пруду. Имеется возможность устроить его в форме полувыемки — полунасыпи (рис. 46). В таком случае наиболее экономичным будет такое расположение канала, при котором сечение выемки

Рис. 46

равновелико сечению насыпи (не нужно будет ни отвозить, ни подвозить грунт). Определите, какой должна быть при этом глубина выемки, если общая глубина канала h = 2м, ширина по дну b = 1м, ширина гребня выемки а = 1м, а угол наклона откосов—45°.

Решение. Пусть х — глубина выемки. Тогда площадь поперечного сечения выемки 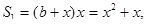площадь сечения насыпи 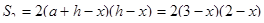. Приравняв площади, получим квадратное уравнение. Решив его, найдем х = 1,2м.

3.13. В различных расчетах по эксплуатации оросительных систем встречается величина R = 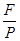гидравлический радиус канала, где F — площадь поперечного сечения канала (живое сечение), Р — длина границы этого сечения (смоченный периметр). Найдите гидравлический радиус канала (рис. 47), проложенного каналокопателем Д — 716 ( AD = 260 см, ВС = 60 см, ABC = BCD = 135°).

Рис. 47

3.14. С помощью теоретических расчетов и эксперимента установлено, что из всех каналов с заданным живым сечением наибольшей пропускной способностью и одновременно наименьшей фильтрацией отличаются каналы с наименьшим смоченным периметром. Про такие каналы говорят, что они имеют гидравлически наивыгоднейший профиль.

Сечение канала — равнобедренный треугольник. Каким должен быть угол при вершине, чтобы канал имел гидравлически наивыгоднейший профиль?

Решение. Пусть F — живое сечение канала, х — величина угла при его вершине, а — длина боковой стороны треугольника. Так как F = 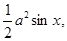Р = 2а, то

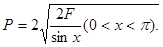
Смоченный периметр Р будет наименьшим, когда 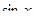будет наибольшим, т.е. при х = 90°.

3.15. Для хранения зерна на элеваторах часто сооружают емкости в форме цилиндров [4]. При этом строят сразу несколько таких емкостей, примыкающих друг к другу в определенном порядке, а также в некоторых местах сооружают дополнительные круглые стенки. Получается монолитный корпус с поперечным сечением довольно сложной конструкции. Зерно засыпается не только в цилиндрические емкости (круглые силосы), но и в емкости образовавшиеся между ними (силосы-звездочки). Для расчета емкости силосного корпуса необходимо знать площади сечений всех его силосов.

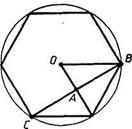
На рисунке 48 изображено поперечное сечение силосного корпуса одного из элеваторов. Найдите площади сечений силосов-звездочек 2 и 3, зная диаметр d силоса 1 и пренебрегая толщиной стенок.

Рис. 48

Решение. Площадь 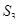равна, очевидно, разности между площадью квадрата ABCD и площадью круга 1:

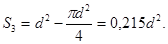
Если от площади квадрата EFGH (которая, очевидно, равна половине площади квадрата 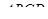) вычесть 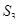, то мы получим учетверенную площадь луночки. Поэтому площадь луночки

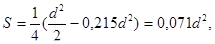
а площадь фигуры 2

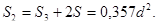
МНОГОГРАННИКИ

3.18. При одном из способов защиты почв от смыва на склонах штампуют лунки в форме прямоугольного параллелепипеда с квадратным основанием (сторона квадрата — 50 см) и высотой 10 см. Определите, сколько литров воды может собраться в такой лунке на склоне под углом наклона 10°, если дополнительно известно, что одна из сторон основания лунки горизонтальна.

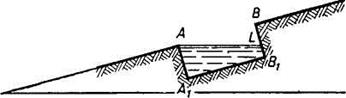
Рис. 51

Решение. Так как (рис. 51) BL = 50tgl0° < 10, то в момент наибольшего наполнения слой воды представляет собой призму высоты 50 см, основанием которой является трапеция 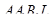. Поэтому объем воды

ТЕЛА ВРАЩЕНИЯ.

3.19. Бревна и дрова на складах лесоматериалов укладывают в штабеля. Учет уложенной в штабеля древесины ведется через объем штабеля с помощью коэффициента полнодревесности, под которым понимается отношение объема древесины в штабеле к геометрическому объему штабеля (первый меньше из-за наличия пустот между стволами). Найдите коэффициент полнодревесности идеализированного прямоугольного штабеля (рис. 52), состоящего из одинаковых цилиндров.

Рис. 52

Решение. Пусть r— радиус основания цилиндра, h — его высота. Допустим, что по ширине штабеля уложено m цилиндров, а по высоте — п. Тогда объем древесины в штабеля

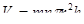Штабель принимается за параллелепипед с измерениями 2 mr , 2 nr и h . Его объем

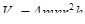значит, коэффициент полнодревесности

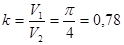Удивительно, что именно такой коэффициент полнодревесности указан в ГОСТ для правильного прямоугольного штабеля из метровых бревен без коры.

3.20. При защите почв от водной эрозии на склонах иногда делают лунки в форме полушара диаметром d. Сколько воды может накопиться в такой лунке на склоне с углом наклона ?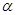

Рис. 53

Решение: Объем воды равен объему (рис. 53) шарового сегмента:

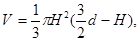
где Н – высота сегмента. Так как расстояние от центра лунки до поверхности воды 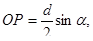то 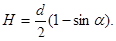Отсюда находим:

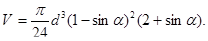
Заключение

Целью данной работы являлось разработка содержания темы «Использование измерений и решение задач на местности при изучении некоторых тем школьного курса геометрии» и методики проведения факультативных занятий. В работе была выдвинута гипотеза исследования, заключающаяся в том, что систематическое и целенаправленное внедрение в школьный курс геометрии разнообразного материала способствует повышению интереса учащихся к геометрии и развивает их творческие способности. В результате естественного педагогического эксперимента гипотеза была подтверждена.

Были решены следующие задачи:

1. Изучена математическая, психолого-педагогическая, методическая литература по проблеме исследования.

2. Подобран и адаптирован для школьников теоретический и практический материал, позволяющий продемонстрировать приложение геометрических фактов к решению задач на местности.

3. Найдены эффективные пути и способы организации факультативных занятий.

4. Разработана методика проведения факультативных занятий по теме «Решение задач на местности».

5. Проведена экспериментальная проверка отобранного материала и методики факультативных занятий.

Практическая значимость исследования заключается в том, что в нем обоснованы возможности совершенствования учебно-воспитательного процесса применительно к процессу преподавания математики путем проведения факультативных занятий, разработаны рекомендации по совершенствованию организационно-педагогического обеспечения математических факультативов. Предложенные научно - методические материалы при использовании в массовой практике позволяют находить эффективные пути организации математических факультативов. Разработанные материалы могут быть использованы студентами физико-математических факультетов при изучении методики преподавания и на педагогической практике, а так же учителями средних школ при организации и проведении уроков.

На основе изучения педагогической, методико-математической, психолого-педагогической литературы, а также опыта работы учителей по вопросу организаций факультативных занятий и непосредственной работы с учителями общеобразовательных школ разработаны рекомендации для успешного функционирования математического факультатива в средней школе.

Важной задачей является раскрытие психолого-педагогических основ организации факультативных занятий как осуществление профильной дифференциации.

Основным направлением предложенных рекомендаций, является максимальное повышение эффективности работы факультативных занятий.

Современная общеобразовательная школа ставит задачу профориентации учащихся по окончании школы, путем введения факультативной формы работы. В работе сформулированы рекомендации, которые повысят уровень преподавания факультативных занятий и тем самым повысят уровень подготовленности учащихся.

Литература

1. Бабанский Ю.К. Оптимизация процесса обучения: Общедидактический

аспект. – М., 1977.

2. Балк М.Б., Балк Г.Д. Математика после уроков, М., Просвещение, 1977.

3. Балк М.Б., Балк Г.Д. Математический факультатив вчера, сегодня, завтра

//Математика в школе – 1987 - №5.

4. Бенбяминов М.Р. Математика и сельское хозяйство, М., 1968.

5. Вилянкин Н.Я., Шибасов Л.Т., Шибасова З.Ф. За страницами учебника

математики: Арифметика. Алгебра. Геометрия. – М.: Просвещение:

АО «Учеб. мет.», 1996.

6. Ганьшин В.Н. Простейшие измерения на местности, М., 1973 – 126 с.

7. Гильбух Ю., Кондратенко Л., Коробко С. Как не убить талант? //Народное

образование. – 1991. - №4.

8. Геометрия. Учебное пособие для 9 и 10 классов средней школы. М., 1979.

9. Депман И.Я., Виленкин Н. Я. За страницами учебника математики. – М. -:

Просвещение, 1989.

10. Занимательная алгебра. Занимательная геометрия. / Я.И. Перьльман. –

Ростов н/Д: ЗАО «Книга», 2005.

11. Иваньков П.А. Основы геодезии , топографии и картографии.-М., 1972

12. Иванов П.А. Технические измерения М., 1964

13. Калмыкова З.И. Типологические принципы развивающегося обучения.-

М.: Знание, 1979.

14. Методика преподавания математики в средней школе. Частная методика:

Учеб. пособие для студентов пед. ин-тов по физ.-мат. спец./А.Я.Блох,

В.А. Гусев, Г.В. Дорофеев и др.; Сост. В.И. Мишин. – М.: Просвеще-

ние, 1987.

15. Методика преподавания математики в средней школе. Общая методика:

Учеб. пособие для студентов физ.-мат. фак. пед. институтов / В.А. Ога-

несян, Ю.М. Колягин, Г.Л. Луканкин, В.Я. Саннинский. – 2-е изд., пе-

раб. и доп. – М.: Просвещение, 1980.

16. Морозова Н.Г. Учителю о познавательном интересе. М.: Знание, серия

«Педагогика и психология», 1979.

17. Педагогическая энциклопедия: в 2-х т./ Под ред. И.А. Каирова, Ф.Н. Пет-

рова. – М.: Советская энциклопедия, 1964. – Т.1.

18. Педагогическая энциклопедия: в 2-х т./ Под ред. И.А. Каирова, Ф.Н. Пет-

рова. – М.: Советская энциклопедия, 1964. – Т.2.

19. Петров В.А. Преподавание математики в сельской школе: Кн. для учите-

ля. – М..6 Просвещение, 1986.

20. Погорелов А.В. Геометрия. М., 1990.

21. Сергеев И.Н., Олехник С.Н., Гашков С.Б. Примени математику. – М.,

Наука, 1989.

22. Чичигин В.Г. Методика преподавания геометрии: Планиметрия. – М.:

Учпедгиз, 1959.

23. Четверухин Н.Ф. Методы геметрических построений, М., Учпедгиз, 1952.

24. Шварцбурд С.И. и др. Состояние и перспективы факультативных занятий

по математике: пособие для учителя. – М., 1977.