Таблица 7 – Исходные данные для стержня Rod57
| Продольное усилие N, Н | Поперечное усилие Qу, Н | Поперечное усилие Qx, Н | Момент кручения Т, Н м | Изгибающий момент Му, Н м | Изгибающий момент Мх, Н м |
| -105192,73 | -9142,98 | -24310,09 | -951,838 | 16813,796 | 99509,169 |
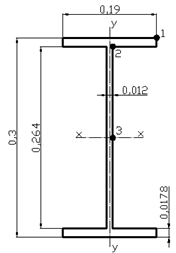
Рисунок 21 – Геометрические характеристики сечения стержня Rod57
Условие прочности [5]:
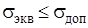 , (22)
, (22)
где 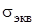 - эквивалентные напряжения, МПа [5];
- эквивалентные напряжения, МПа [5]; 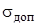 - допускаемые напряжения, МПа [5].
- допускаемые напряжения, МПа [5].
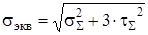 , (23)
, (23)
где 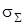 - суммарные нормальные напряжения, МПа [5];
- суммарные нормальные напряжения, МПа [5]; 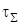 - суммарные касательные напряжения, МПа [5].
- суммарные касательные напряжения, МПа [5].
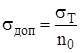 , (24)
, (24)
где 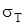 - предел текучести стали,
- предел текучести стали, 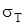 =305 МПа [3]; n0 – коэффициент запаса прочности стали, n0=1,4 [3].
=305 МПа [3]; n0 – коэффициент запаса прочности стали, n0=1,4 [3].
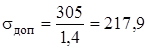 МПа.
МПа.
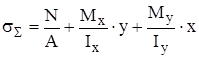 , (25)
, (25)
где А - площадь сечения, м2 [5] ; Iх - момент инерции относительно главной центральной оси х-х, м [5]; у – расстояние от главной центральной оси х-х до рассматриваемой точки, м [5]; Iу - момент инерции относительно главной центральной оси у-у, м4 [5] ; х – расстояние от главной центральной оси у-у до рассматриваемой точки, м [5].
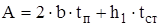 , (26)
, (26)
где b – ширина сечения, b=0,19 м [5]; tп – толщина полки, tп = 0,0178 м [5]; h1 – расстояние между полками, h1=0,264 м [5]; tст – толщина стенки, tcт=0,012 м [5].
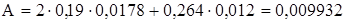 м2.
м2.
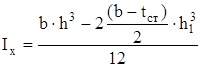 , (27)
, (27)
где h – высота сечения, h=0,3 м.
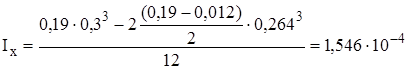 м4.
м4.
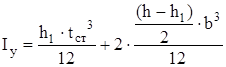 , (28)
, (28)
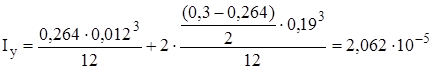 м4.
м4.
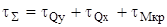 , (29)
, (29)
где 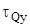 - касательные напряжения от действия поперечной силы Qy, МПа [5];
- касательные напряжения от действия поперечной силы Qy, МПа [5];
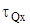 - касательные напряжения от действия поперечной силы Qх, МПа [5];
- касательные напряжения от действия поперечной силы Qх, МПа [5]; 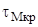 - касательные напряжения от действия момента кручения Мкр, МПа [5].
- касательные напряжения от действия момента кручения Мкр, МПа [5].
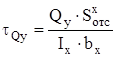 , (30)
, (30)
где 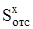 - статический момент отсеченной части, м3 [5]; bx – ширина рассеченной части, м [5].
- статический момент отсеченной части, м3 [5]; bx – ширина рассеченной части, м [5].
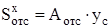 , (31)
, (31)
где Аотс – площадь отсеченной части сечения для рассматриваемой точки, м2 [5]; ус – расстояние от оси х-х до центра тяжести отсеченной части, м [5];.
Схемы для определения статического момента приведены на рисунках 21 и 22.
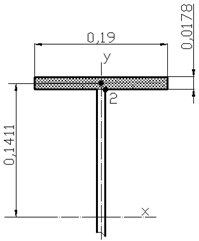
Рисунок 22 - Схема к определению статического момента для точки 2
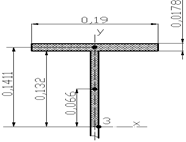 |
Рисунок 23 - Схема к определению статического момента для точки 3
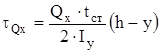 , (32)
, (32)
где h – высота рассматриваемого сечения, м [5]; у – расстояние от главной центральной оси х-х до рассматриваемой точки, м [5].
Касательные напряжения 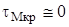 , так как величина действующего момента кручения Мкр в рассматриваемых стержнях имеет весьма малое значение.
, так как величина действующего момента кручения Мкр в рассматриваемых стержнях имеет весьма малое значение.
Расчет эквивалентных напряжения для точки 1
Суммарные нормальные напряжения по формуле (25) при y=0,15 м, x = 0,095 м:
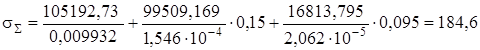 МПа.
МПа.
Статический момент по формуле (31) Sотс=0 при Аотс = 0.
Касательные напряжения по формуле (32) при tст=0,012 м, h=0,3 м, y=0,15 м:
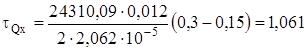 МПа.
МПа.
Суммарные касательные напряжения по формуле (29) 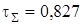 МПа.
МПа.
Эквивалентные напряжения по формуле (23):
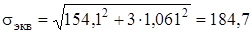 МПа.
МПа.
Расчет эквивалентных напряжения для точки 2
Суммарные нормальные напряжения по формуле (25) при y=0,132 м, х=0,006 м:
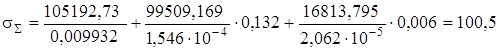 МПа.
МПа.
Площадь отсеченной части:
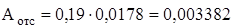 м2.
м2.
Статический момент по формуле (31) при ус=0,1411м:
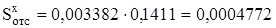 м3.
м3.
Касательные напряжения по формуле (30) при 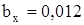 м,
м,
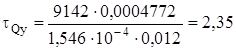 МПа.
МПа.
Касательные напряжения по формуле (32) при tст=0,012 м, h=0,3 м, y=0,15 м:
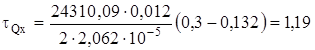 МПа.
МПа.
Суммарные касательные напряжения по формуле (29):
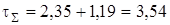 МПа.
МПа.
Эквивалентные напряжения по формуле (23):
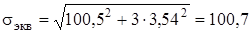 МПа.
МПа.
Дата: 2019-05-28, просмотров: 311.