Каждому определенному значению первого признака соответствует много значений другой переменной. Такая связь называется корреляционной связью. Корреляционная связь проявляется лишь в среднем для всей совокупности наблюдений. В отношении же отдельных наблюдений она очень неполна и неточна. Известно, например, что существует корреляция между весом животного и его высотой. Это означает, что более высокие животные обычно тяжелее более низких. Но полного соответствия между значениями этих признаков нет. Поэтому различают положительную и отрицательную корреляции. При положительной корреляции зависимость между признаками прямая: при увеличении одного увеличивается и другой. При отрицательной корреляции зависимость между признаками обратная: увеличение одного признака соответственно связано с уменьшением другого. В случае качественных признаков отрицательная корреляция будет обозначать, что присутствие одного признака преимущественно совпадает с отсутствием другого, а при положительной — присутствие одного преимущественно совпадает с присутствием другого. Корялиционную связь можно определить с помощью коэфициента корреляции.
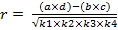 где а,b,c,d,-количество особей с тем или иным признаком. Коэффициенты корреляции могут колебаться от 0 до + 1 при положительной корреляции и от 0 до — 1 при отрицательной корреляции. Если r = О, то это означает, что вариация обоих признаков происходит независимо. При значениях r ≠ О вариации обоих признаков взаимосвязаны, т. е. с изменением одного признака меняется и другой (в том же направлении — при положительной корреляции и в противоположном направлении — при отрицательной корреляции).
где а,b,c,d,-количество особей с тем или иным признаком. Коэффициенты корреляции могут колебаться от 0 до + 1 при положительной корреляции и от 0 до — 1 при отрицательной корреляции. Если r = О, то это означает, что вариация обоих признаков происходит независимо. При значениях r ≠ О вариации обоих признаков взаимосвязаны, т. е. с изменением одного признака меняется и другой (в том же направлении — при положительной корреляции и в противоположном направлении — при отрицательной корреляции).
24. Вычисление коэффициента и ошибки корреляции. Показать на примере.
ПО ЛЕКЦИИ
Коэффициент корреляции - это статистический показатель зависимости двух случайных величин. Коэффициент корреляции может принимать значения от -1 до +1. При этом, значение -1 будет говорить об отсутствии корреляции между величинами, 0 - о нулевой корреляции, а +1 - о полной корреляции величин. Т.е., че ближе значение коэффициента корреляции к +1, тем сильнее связь между двумя случайными величинами.
Взято два показателя:
- Вес многолетних растений (у)
- Кустистость (х)
Для вычисления коэфф.корреляции необходимо вычислить отклонение от среднего – ах и ау
| х | 4 | 6 | 10 | 12 | СРЕДНЕЕ 8 |
| у | 30 | 34 | 42 | 46 | СРЕДНЕЕ 38 |
Вычислим отклонение от среднего (х – СРЕДНЕЕ или у –СРЕДНЕЕ) т.е 8-4 или 38-30 и т.д.
| ах | -4 | -2 | 2 | 4 | |
| ау | -8 | -4 | 4 | 8 | |
| ах * ау | 32 | 8 | 8 | 32 | Сумма = 80 |
Так как сумма 80, то значит корреляция положительная
Возведем в квадрат значения отклонения от среднего по обоим рядам и суммируем их
| ряд ах: а2х | 16 | 4 | 4 | 16 | СУММА 40 |
| ряд ау а2у | 64 | 16 | 16 | 64 | СУММА 160 |
r = (сумма ах * ау) / корень из (сумма а2х * сумма а2у) = 80 / корень из (160 * 40) = 80/80 = 1
ЗНАЧИТ КОРРЕЛЯЦИЯ ПОЛНАЯ
Далее найдем ошибку:
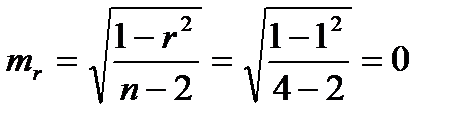 ,
,
НЕ ПО ЛЕКЦИИ
Коэффициент корреляции призван численно выражать долю сопряженной вариации двух признаков в общей их вариации:
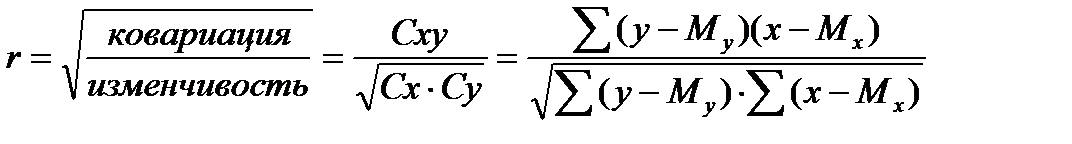 ,
,
где Cxy – характеристика сопряженной изменчивости признаков,
Cx, Cy – характеристика общей изменчивости признаков.
При большом количестве данных коэффициент корреляции имеет смысл вычислять на компьютере (например, с помощью функции КОРРЕЛ в среде программы Excel), но для небольших выборок его можно быстро найти и при ручном счете. Рабочая формула для расчетов имеет вид:
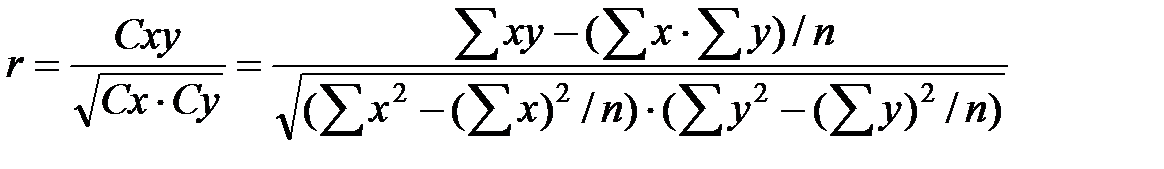 .
.
Способ вычисления коэффициента корреляции показан в таблице 13 на примере зависимости между живым весом коров (х) и их приплода (у, кг). По таблице рассчитываются квадраты вариант и их произведения, а также суммы вариант, квадратов и произведений. Вычисления ведутся по точным рабочим формулам.
Таблица 13
| i | у | х | у² | х² | х ∙ у |
| 1 | 4 | 30 | 16 | 900 | 120 |
| 2 | 6 | 34 | 36 | 1156 | 204 |
| 3 | 10 | 42 | 100 | 1764 | 420 |
| 4 | 12 | 46 | 144 | 2116 | 552 |
| Σ | 32 | 152 | 296 | 5936 | 1296 |
Проведем последовательные расчеты. Сначала определим вспомогательные величины:
Cxy = Σ(x∙y)−(Σx)∙(Σy) / n = 1296 − 152 ∙ 32 / 4 = 80,
Cy = Σy² − (Σy)² / n = 296 – 32*32/4 = 40
Cx = Σx² − (Σx)² / n = 5936 – 152*152\4 = 160
затем – коэффициент корреляции:
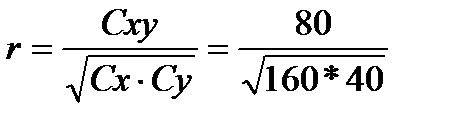 = 1
= 1
Далее найдем его ошибку:
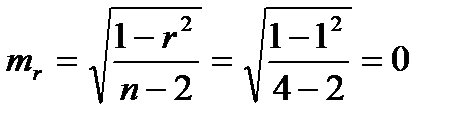 ,
,
Я НЕ ЗНАЮ ЧТО ЕЙ НАДО, ТАМ ЕЩЕ ЕСТЬ МИЛЛИОН СПОСОБОВ
25. Достоверность разницы между попарными данными. Привести пример.
ОНА ТАК ДИКТОВАЛА
Иногда данные одной особи соответствуют данным другой, желательно чтоб особи были однородными.
Если особи разного пола, то результаты данных могут быть разными. Тогда сравнения проводятся попарно до воздействия и после. Проявления признака зависят от пары, в этих случаях мы проводим не только определение разности, но и ошибку.
Пример:
Животных кормили витамином б12 и проводили сравнительный анализ, исследовали 7 коров. Известны данные в их убойном весе (кг) в теплом состоянии – х, и после охлаждения – у.
| x | 322.6 | 250.6 | 287.3 | 408.1 | 338 | 213.5 | 323.3 | |||
| y | 318.9 | 247 | 279.7 | 403 | 334.7 | 209.3 | 319.2 | |||
| d = (x-y) | 3.7 | 3.6 | 7.6 | 5.1 | 3.3 | 4.2 | 4.1 | СУММА = 31.6 | ||
| Md = (СУММА d)/ n = 31.6/7 | 4.5 | |||||||||
| d – Md | -0.8 | -0.9 | 3.1 | 0.6 | -1.2 | -0.3 | -0.4 | |||
| (d – Md)2 | 0.64 | 0.81 | 9.69 | 0.36 | 1.44 | 0.09 | 0.16 | СУММА = 13.1 | ||
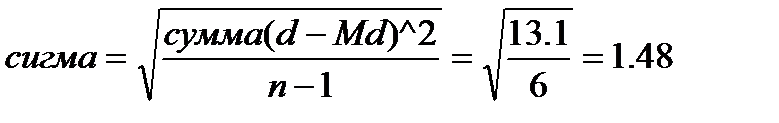 ,
,
Это значит, что вариабельность маленькая, изменчивости нет.
mMd (ошибка средней разности) = сигма\корень из n = 1.48/2.65 = 0.56
td (разность критерия стьюдента) = Md/mMd = 4.5/0.56 = 8.04
ню = n1 + n2 - 2 = 7 + 7 – 2 = 12
находим по таблице {2.2; 3.1; 4.2}
8.04 подходит к последнему значению (хз почему, она так сказала…)
ВЫВОД: достигает 3 порог надежности безошибочного прогноза.
Дата: 2019-05-28, просмотров: 439.