Существуют две категории связей, или зависимостей между признаками: функциональные и корреляционные, или статистические. При функциональных зависимостях каждому значению одной переменной величины соответствует одно вполне определённое значение другой переменной. Необходимо учесть, что функциональные связи встречаются только в идеальных условиях, когда предполагается, что никаких посторонних влияний нет. В некоторых случаях такая зависимость проявляется настолько сильно, что при изменении первого признака на определенную величину всегда изменяется и второй признак на определенную величину, поэтому каждому значению первого признака всегда соответствует совершенно определенное, единственное значение второго признака. При изучении живых объектов − диких и культурных растений, животных, микроорганизмов − приходится иметь дело со связями другого рода. Живой организм развивается в связи с условиями его жизни, под действием бесконечно большого числа факторов, которые по-разному определяют развитие разных признаков. Каждому определенному значению первого признака соответствует не одно значение второго признака, а целое распределение этих значений при вполне определенных основных показателях этого частного распределения− средней величины и степени разнообразия. Такая связь называется корреляционной связью или просто корреляцией. Корреляционная связь, например, между весом животных и их длиной выражается в том, что каждому значению длины соответствует определенное распределение веса (а не одно значение веса), и с увеличением длины увеличивается и средний вес животных.

7.Охарактеризуйте выборочную совокупность. Дайте определения понятиям вариационный размах и лимиты.

Выборочная сов-ть – отбор объектов, определенным образом в выборку из генеральной с. Для того, чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность выборка должна обладать свойством репрезентативности. Значение крайних классов называют лимитом. Вариационный размах - разность между максимальным и минимальным значениями признака некоторой совокупности. Данный показатель используется при сравнении объектов наблюдения, их свойств. Он показывает колебания, подвижность свойств объекта, его особенности. Если средние величины (среднее арифметическое, медиана, мода) не показывают влияние особенностей признака (объекта) и представляют их в одной величине, то вариативность, колебания значений признака, влияние каких-либо факторов и особенностей могут быть отражены в виде вариационного размаха, среднего квадратичного отклонения, дисперсии.

8.Опишите свойства средней арифметической величины. Приведите пример вычисления взвешенной средней, гармонической средней.

Эта величина, где сумма +\- отклонений от нее = 0. Обозначается 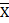. 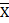=ΣХ\n

Свойства: 1)абстрактная величина 2)конкретная величина - харак-т типичное состояние признаков совокупности. Пример: если кол-во плодов на растении составляет 4,5,9, средняя ариф.=6, отклонение от нее=2,-1,+3, а алгебраическая сумма = 0.

Средняя рассчитанная для значений признака с неодинаковыми весами называется взвешенной средней. Хвзв=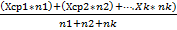

Например, имеются результаты 2-х исследований длины хоботка пчел в одном случае получена средняя длина хоботка 6,6 мм в другом 6 мм. В первом случае измерены хоботки у 100 пчел во втором у 20. Значит Хср=6,6 и Хср=6 их весами являются численности групп n1=100 и n2=20. Хвзв= 6,6*100 + 6*20 / 100+20=6,5 мм. Применяется средняя гармоническая при усреднении меняющихся скоростей.

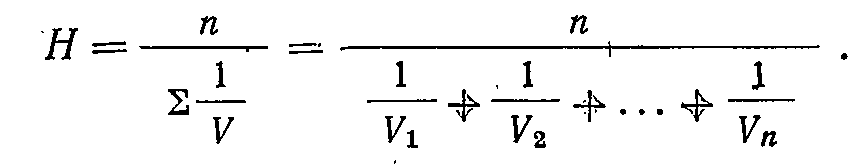
Например: Почтовые голуби одной станции к месту кормежки летят со скоростью 50 км/час, а в обратном направлении — со скоростью 40 км/час. Если ничего больше неизвестно и требуется выяснить среднюю скорость полета для обоих направлений '(расстояния, очевидно, равны), то сделать это можно, рассчитав простую среднюю гармоническую для двух дат 50 и 40:

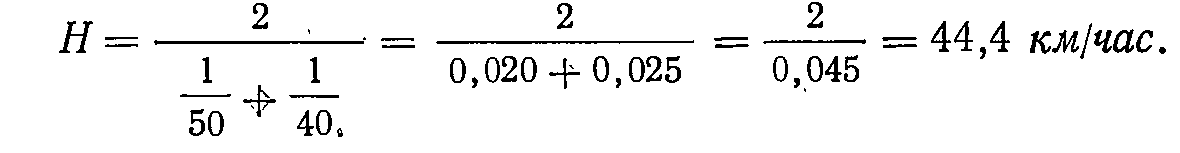
Сред. квадратическое величина (варианца) – является более точным показ-м, характер-м вариацию или рассеивания вариант вокруг среднего ариф., является сумма квадратов отклонений варианцов от сред. значения.