Объясните бимодальные и полимодальные кривые, понятия мода, медиана и их значение, протуберансы ошибок.
Класс\варианта обладающие наибольшей частотой называют модальным. Кривая распределения имеет более одного максимума частоты встречаемости. Такое распределение называется полимодальным. Если распределение имеет два максимума, оно называется бимодальным. Значение крайних классов называют лимитом. По вариационному ряду можно найти модальный класс, который соответствует большая частота. Непараметрическими характеристиками положения являются мода и медиана.
Модой (Mo) называется варианта, имеющая наибольшую частоту или относительную частоту. Медианой (Me) называется варианта, которая делит вариационный ряд на две части, равные по числу вариант. Иногда наблюдается резкое снижение или возрастание частоты отдельных вариант.
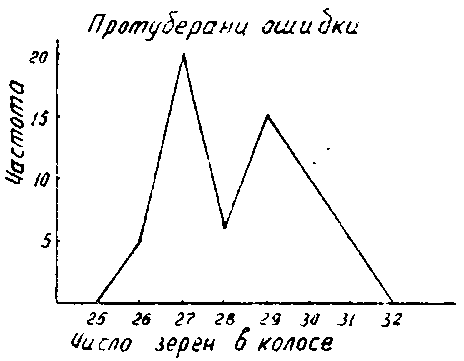
Такие выступы на кривых называются протуберанцами ошибок. Причины их возникновения: 1. Недостаточное количество объектов исследования. 2. Слишком мелкие градации изучаемых признаков. 3. Допущенные ошибки в измерениях или подсчетах.
Опишите основные параметры, характеризующие генеральную совокупность и выборку.
Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение (σ). Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной. Точечной оценкой генеральной средней является выборочное среднее. Выборочным средним называется среднее арифметическое значение признака выборочной совокупности. Выборочное среднее является основной характеристикой положения, показывает центр распределения совокупности, позволяет охарактеризовать исследуемую совокупность одним числом, проследить тенденцию развития, сравнить различные совокупности (выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0). Выборочная средняя по формуле:
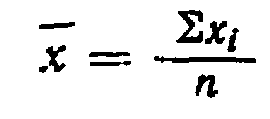
Постройте корреляционную решетку для составления сгруппированного вариационного ряда.
КОРОЧЕ ТУТ ОТВЕТ БУДЕТ ТАКОЙ ЖЕ, КАК И В 19, НО ВМЕСТО ЕДИНИЧНЫХ ЦИФР НАПИШИТЕ ГРУППЫ (НАПРИМЕР, 4-9, 6-11, 10-15, 12-17 ЭТО КУСТИСТОСТЬ. 30-35, 34-39, 42-47, 46-51 ЭТО ВЕС РАСТЕНИЙ) ОСТАЛЬНОЕ ВСЕ ТАКЖЕ
(3-блок)
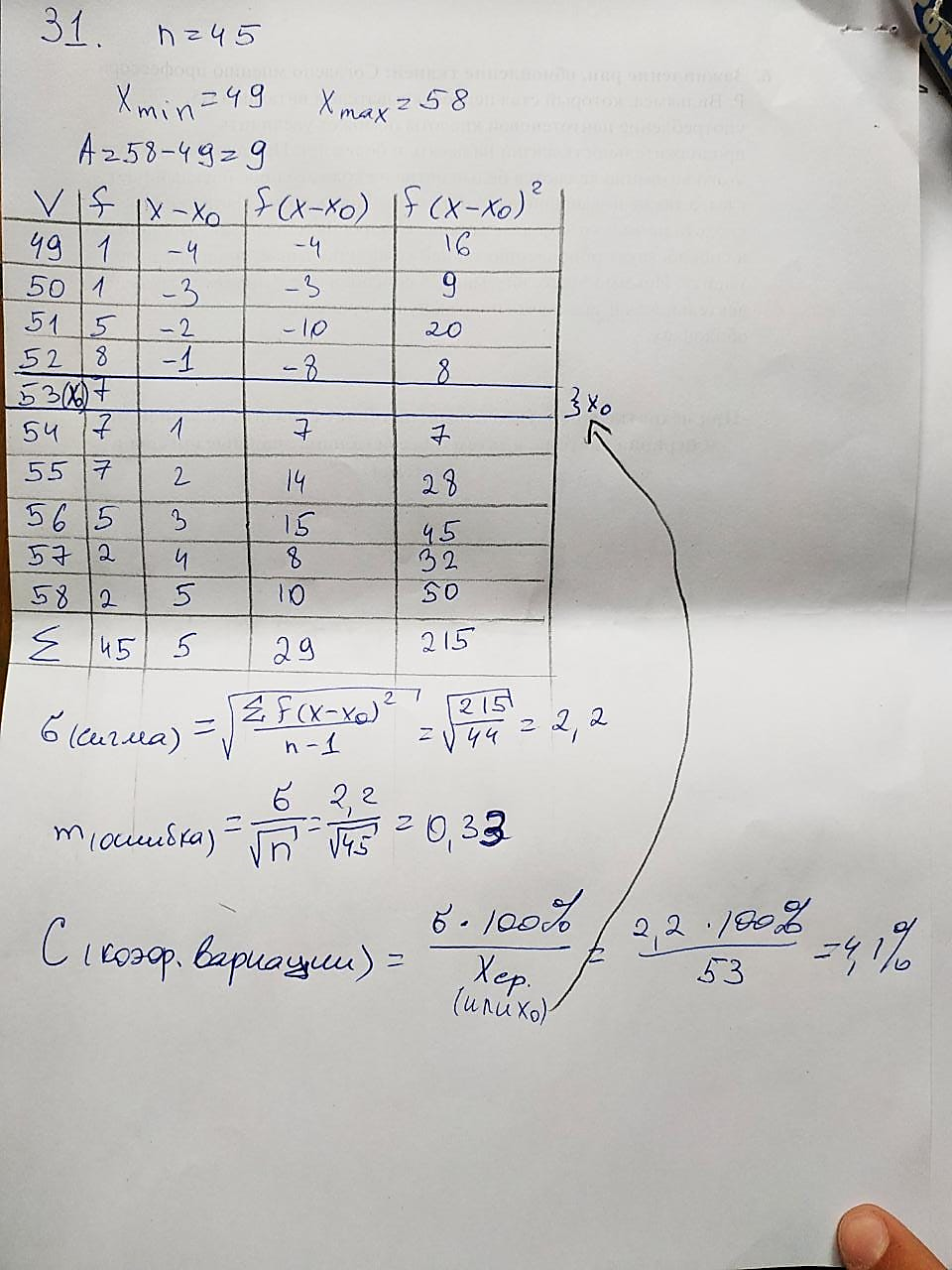
31. Было подсчитано число лучей в хвостовых плавниках камбалы:
53 54 51 52 56 52 54 55 53 58 51 53 51 55 55 51 56 52 54 57 52 52 56 53 50 55 54 53 55 57 55 53 54 53 54 52 55 52 52 58 56 51 54 56 49
Составьте вариационный ряд и начертите полигон распределения. Вычислите Х, m, CV.
32. В 400 квадратах гемоцитомера было подсчитано число дрожжевых клеток:
6 4 6 4 5 3 6 6 5 5 3 6 4 2 2 2 3 7 4 3 1 4 5 6 1 7 5 5 5 3 3 6 7 2 6 6 7 4 1 3 12 5 1 5 4 2 4 5 5 7 4
12 10 14 14 13 12 12 12 15 13 11 12 12 14 12 11 13 12 13 14 11 13 14 12 13 12 12 14 12 14 13 13 12 13 12 13 12 11 11 12 13 14 12 14 13 14 13 12 14 15 10 11 10 11 15 11 16 11 11 11
4 5 4 5 5 6 1 6 4 4 6 4 6 2 3 4 5 5 6 4 5 4 6 4 5 5 5 4 6 7 5 4 4 2 4 5 5 5 5 4 5 5 6 6 4 5 7 5 5 5
Х 68 65 63 66 66 65 65 65 65 64 66 67 63 64 69 69 65 69 67 68 61 69 61 64 62 66 59 65 62 68 61 67 69 69 66 66 71 67 65
У 40 40 40 40 40 41 39 41 39 40 40 42 38 43 41 41 40 40 41 45 40 38 37 38 37 39 37 39 38 40 41 39 41 40 50 40 40 39 44 41
Х 6 7 5 6 5 5 4 5 5 4 6 7 6 5 6 6 7 5 6 6 7 3 6 7 4 5 5 5 6 5 6 4 5 7 7 6 6 6 5 7 6 5 4 6 5 5 6 6 5 6 8
У 4 5 4 4 6 2 3 3 2 6 6 9 7 2 4 7 5 6 8 10 4 5 5 4 2 4 5 6 5 9 3 6 4 3 4 2 5 7 3 5 4 5 3 7 2 3 2 5 3 7 4
Получены следующие данные о продолжительности беременности у кроликов при различных размерах помета (число крольчат в помете Х и длительность беременности в днях У). Есть ли корреляция между признаками?
Х 1 8 3 5 7 8 4 8 3 4 4 8 8 5 7 6 6 5 6 6 6 5 7 8 10 6 7 6 7 6 5 10 7 8 8 6 5 6 5 4
У 33 30 31 31 31 32 31 31 32 33 32 31 31 31 31 30 31 32 32 31 32 32 31 32 31 31 30 31 31 32 31 30 32 32 31 31 31 32 30 31
| X | Y | Dx | Dy | DxDy | Dx^2 | Dy^2 |
| 1 | 33 | -5,10 | 1,8 | -9,18 | 26,01 | 3,24 |
| 8 | 30 | 1,90 | -1,2 | -2,28 | 3,61 | 1,44 |
| 3 | 31 | -3,10 | -0,2 | 0,62 | 9,61 | 0,04 |
| 5 | 31 | -1,10 | -0,2 | 0,22 | 1,21 | 0,04 |
| 7 | 31 | 0,90 | -0,2 | -0,18 | 0,81 | 0,04 |
| 8 | 32 | 1,90 | 0,8 | 1,52 | 3,61 | 0,64 |
| 4 | 31 | -2,10 | -0,2 | 0,42 | 4,41 | 0,04 |
| 8 | 31 | 1,90 | -0,2 | -0,38 | 3,61 | 0,04 |
| 3 | 32 | -3,10 | 0,8 | -2,48 | 9,61 | 0,64 |
| 4 | 33 | -2,10 | 1,8 | -3,78 | 4,41 | 3,24 |
| 4 | 32 | -2,10 | 0,8 | -1,68 | 4,41 | 0,64 |
| 8 | 31 | 1,90 | -0,2 | -0,38 | 3,61 | 0,04 |
| 8 | 31 | 1,90 | -0,2 | -0,38 | 3,61 | 0,04 |
| 5 | 31 | -1,10 | -0,2 | 0,22 | 1,21 | 0,04 |
| 7 | 31 | 0,90 | -0,2 | -0,18 | 0,81 | 0,04 |
| 6 | 30 | -0,10 | -1,2 | 0,12 | 0,01 | 1,44 |
| 6 | 31 | -0,10 | -0,2 | 0,02 | 0,01 | 0,04 |
| 5 | 32 | -1,10 | 0,8 | -0,88 | 1,21 | 0,64 |
| 6 | 32 | -0,10 | 0,8 | -0,08 | 0,01 | 0,64 |
| 6 | 31 | -0,10 | -0,2 | 0,02 | 0,01 | 0,04 |
| 6 | 32 | -0,10 | 0,8 | -0,08 | 0,01 | 0,64 |
| 5 | 32 | -1,10 | 0,8 | -0,88 | 1,21 | 0,64 |
| 7 | 31 | 0,90 | -0,2 | -0,18 | 0,81 | 0,04 |
| 8 | 32 | 1,90 | 0,8 | 1,52 | 3,61 | 0,64 |
| 10 | 31 | 3,90 | -0,2 | -0,78 | 15,21 | 0,04 |
| 6 | 31 | -0,10 | -0,2 | 0,02 | 0,01 | 0,04 |
| 7 | 30 | 0,90 | -1,2 | -1,08 | 0,81 | 1,44 |
| 6 | 31 | -0,10 | -0,2 | 0,02 | 0,01 | 0,04 |
| 7 | 31 | 0,90 | -0,2 | -0,18 | 0,81 | 0,04 |
| 6 | 32 | -0,10 | 0,8 | -0,08 | 0,01 | 0,64 |
| 5 | 31 | -1,10 | -0,2 | 0,22 | 1,21 | 0,04 |
| 10 | 30 | 3,90 | -1,2 | -4,68 | 15,21 | 1,44 |
| 7 | 32 | 0,90 | 0,8 | 0,72 | 0,81 | 0,64 |
| 8 | 32 | 1,90 | 0,8 | 1,52 | 3,61 | 0,64 |
| 8 | 31 | 1,90 | -0,2 | -0,38 | 3,61 | 0,04 |
| 6 | 31 | -0,10 | -0,2 | 0,02 | 0,01 | 0,04 |
| 5 | 31 | -1,10 | -0,2 | 0,22 | 1,21 | 0,04 |
| 6 | 32 | -0,10 | 0,8 | -0,08 | 0,01 | 0,64 |
| 5 | 30 | -1,10 | -1,2 | 1,32 | 1,21 | 1,44 |
| 4 | 31 | -2,10 | -0,2 | 0,42 | 4,41 | 0,04 |
| Mx | My |
|
| ∑DxDy | ∑Dx^2 | ∑Dy^2 |
| 6,1 | 31,275 |
|
| -21,1 | 135,60 | 22,2 |
G=√∑(Dx^2) ∑Dy^2= √3010.3=54.86
R=∑DxDy/G= -21.1/54.86= -0.38 Слабая отрицательная корреляция
45. Было сделано 5 определений содержания кальция в крови (в усл. ед.):
11, 27 11,36 11,09 11,16 11,47. Вычислите Х, σ и m.
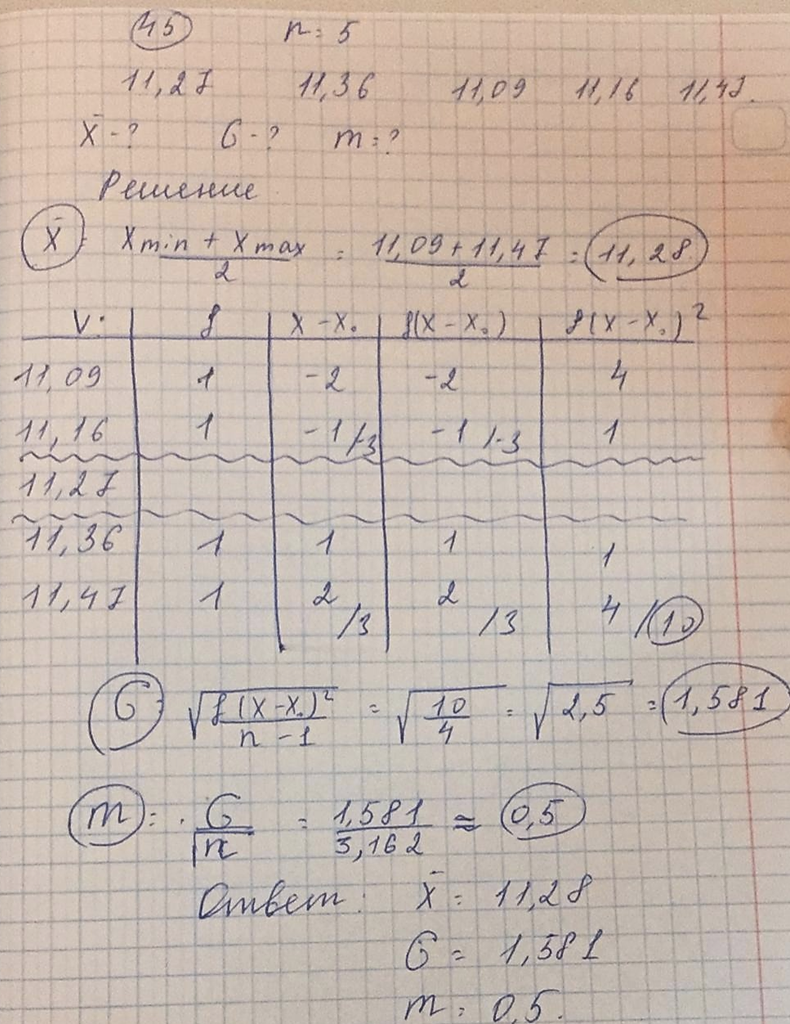
Ответ: σ =1,581
m= 0,5
X= 11,28
46. Температура тела у тушканчиков оказалась следующей:
Самцы: 37,5 37,9 37,4 37,8 36,8 37,8 37,5 37,4 37,8 36,8 37,8
Самки: 37,8 38,1 37,0 37,7 37,7 37,8 37,6 37,7 37,7 37,8 37,6
Х 66, 61, 67, 73, 51, 59, 48, 47, 58, 44, 41, 54, 52, 47, 51, 45
У 38, 31, 36,43, 29, 33, 28, 25, 36, 26, 21, 30, 28, 27, 28, 26
На 10 парах крыс определяли биологическую ценность белков земляного ореха сырого Р и жаренного О. Пары данных следующие: 61-55, 60-54, 56-47, 63-59, 56-51, 63-61, 59-57, 56-54, 44-63, 61-58. Достоверна ли разница?
50. Получены следующие данные о длине крыльев у двух видов скворцов (в мм):
St. contra 120 120 121 122 125 126 126 125 122 123 122
St. ginginiamus 129 123 128 125 126 127 129 125 124 129 128 127 127
В возрасте двух месяцев мыши обычной лабораторной линии весили 23 г и имели фенотипическую вариансу, равную 6.55. После многих поколений инбридинга и отбора удалось выделить карликовую линию, средний вес 12 г, фенотипическая варианса равна 2.92. Определите коэффициент вариации и сделайте выводы.
Напишите им что тут нет ни количества мышей чтобы шаг определить и построить ряд, ни таблицы значений чтобы можно было решетку сделать!
Или, если решите, будем благодарны.
Дайте определение понятию «вариабельность» с точки зрения биометрии. Опишите варьирующие признаки и их учет, группировку первичных данных.
Изучаемые признаки имеют разное значение и здесь возникает вариабельность - степень различий между наблюдениями. Это свойство присуще всем, выражающееся в «случайной», непредсказуемой изменчивости. Все биологические признаки делятся на качественные (не поддаются непосредственному измерению и учитываются по наличию их свойств у отдельных членов изучаемой группы) и количественные (поддаются измерению или счету). Существует много различных форм и способов учета, например, условиях лабораторного эксперимента результаты фиксируют в протоколах, учетных бланках и других формулярах. Процесс систематизации результатов массовых наблюдений, объединения их в относительно однородные группы по некоторому признаку называется группировкой. Особую форму группировки представляют так называемый вариационный ряд – это ранжированный двойной ряд чисел, показывающий каким образом числовые значения признака связаны с их повторяемостью в данной совокупности. Для составления вариационного ряда необходимо: Найти в учетах данных максимальное (max) и минимальное (min) значения признака, размах изменчивости признака (lim = max-min). Исходя из объема выборки и размаха изменчивости, выбрать оптимальное число классов (k) для проведения группировки. На основании выбранного количества классов и размаха изменчивости установить величину классового промежутка (i). Осуществить разноску частот по классам.
2.Опишите способы отбора объектов в выборку, правила записи данных. Дайте определение понятиям: "варианта", "частота" и укажите их обозначение.
Совокупность – всякое множество отдельных, отличных друг от друга и сходных где-то объектов. Значение – числовой\иной показатель для определения совокупности, называют вариантой (Х). Ряд вариант – Х1,Х2…Х30. В статистике частота (f) - это цифра, показывающая, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта, либо наблюдаемый параметр достигал данной величины. Генеральная совок-ть – общая, теоретически приближенная к бесконечности, т.е. совокупность всех единиц, которые к ней относятся. Выборочная сов-ть – отбор объектов, определенным образом в выборку из генеральной с.
Типы выборок (в зависимости от задач исследования и объекта):
1)случайный повторный отбор – из генеральной без учета развития изучаемого признака
2)случайный бесповторный – не попадают в выборку и в генеральной. Используются при исследовании редких форм рас\жив.
3)серийный(гнездовый) отбор – при этом генеральная разбивается на части, серии, некоторые из них исследуются целиком. Используется в экспериментальных опытах
4)механический – разновидность случайного отбора, заключающийся в том, что отбор единиц производится в мех. порядке
5)типический (пропорциональный) отбор – необходимый для численности единиц. Генеральная разбивается на однородные группы.
3.Дайте определение и приведите пример составления простых и сложных вариационных рядов, и их графическое изображение (полигон распределения, гистограмма).
Вариационный ряд – это ранжированный в порядке +\- ряд вариант с соответствующей им частотам. Это двойной числовой ряд. Его можно изобразить графически (вар.кривая).
Простой - это ряд, в котором каждая варианта встречается только по одному разу (все частоты при этом равны 1)
Взвешенный(сложный) - ряд, в котором одна или несколько вариант встречаются неоднократно.
На оси абсцисс – классы, на ординат – частоты. Пример: n=30.
| Х | F |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 1 |
limmax-1 limmin-4 n= Σf=30. (простая кривая)
Исследуя непрерывную изменчивость, а также анализируя данные при непрерывной изменчивости с большим размахом варьирующая амплитуда > 12, варианты разбиваем на классы. При соблюдении правил: 1) границы классов должны быть такими, чтобы каждая варианта была отнесена к одному классу. 2)размеры классов должны быть равными 3)1 и послед. классы могут быть неполными 4)кол-во классов не должно быть >10-15, не < 7.
Размер интервального промежутка – l, l=А/К -1, А=limmax-limmin.
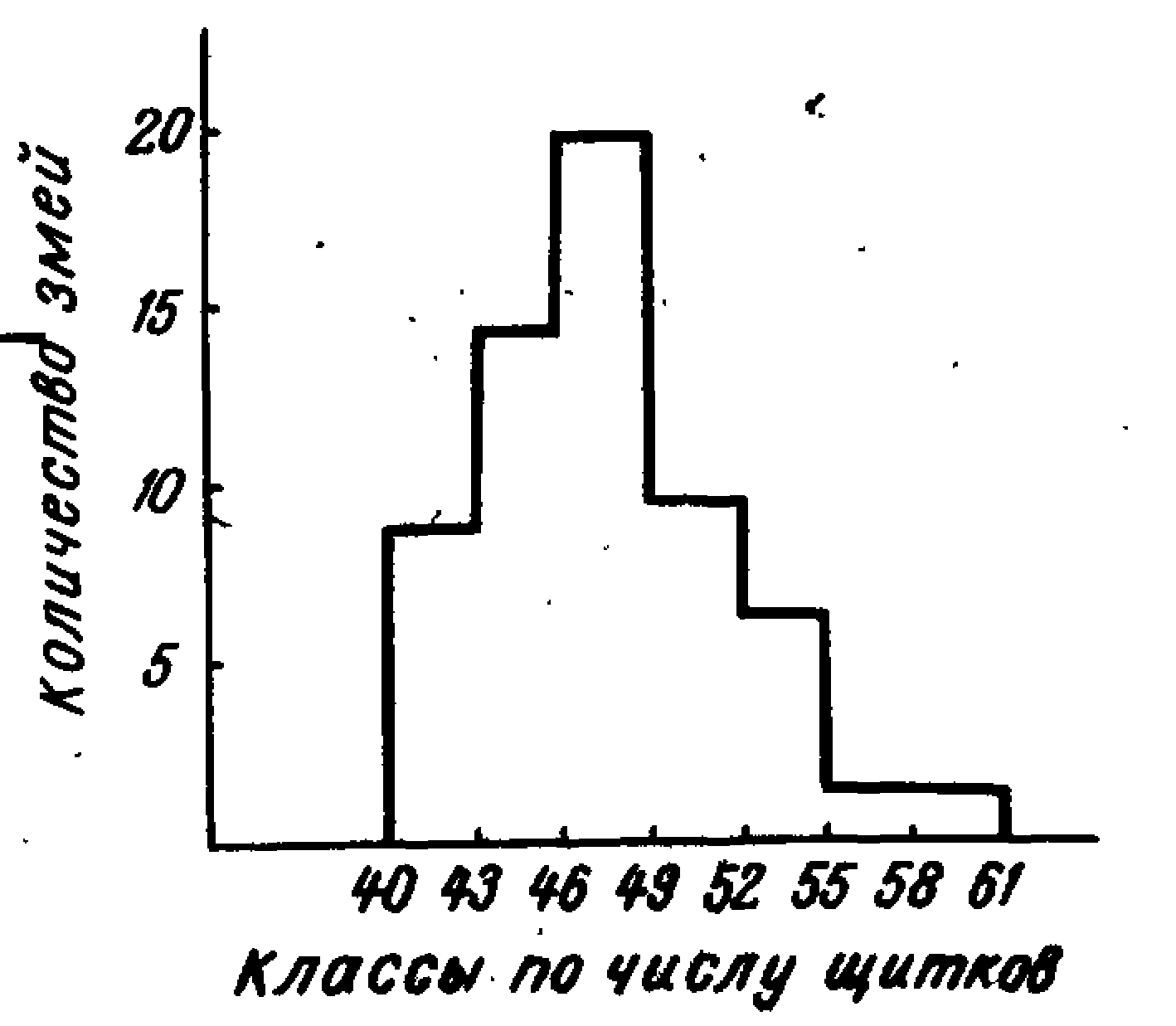Пример: 40 растений кукурузы. Max=179см, min=100см. А=79. L=79\6=13-1=12
| W | F |
| 100-112 | 1 |
| 113-125 | 2 |
| 126-138 | 4 |
| 139-151 | 4 |
| 152-163 | 2 |
| 164-176 | 1 |
(гистограмма)
Гистограмма-вариационный ряд представленный в виде диаграммы, в которой различная величина частот изображается различной высотой столбиков.
Дата: 2019-05-28, просмотров: 548.
