Категории ошибок бывает А и В.
А) Ошибки, которые нельзя учесть статистическими методами, но избежать или свести их к минимуму можно хорошей организацией исследования.
1 Ошибки методические возникают при применении неправильной методики сбора и обработки материалов, при неточном проведении химических анализов, при невыравненности общих условий жизни для контрольной и опытной групп и т. п.
2 Ошибки точности – это пороки первичной регистрации фактов, измерение непроверенными, испорченными инструментами, расчеты с недостаточной, а также и с избыточной ненужной точностью.
3 Ошибки случайные – описки, просчеты, перепутывание материалов, опечатки.
4 Ошибки типичности возникают главным образом в начальных стадиях экспериментов и наблюдений. Это особенно опасный вид ошибок, происходящих оттого, что в выборку отбирается группа объектов, нетипичная для всей генеральной совокупности, и по такой выборке делаются прогнозы на всю генеральную совокупность, вследствие чего получается сильно искаженная характеристика всей массы объектов изучаемой категории. Б) Ошибки, учитываемые статистическими методами, но неустранимые при проведении любого биологического исследования.
Ошибки репрезентативности возникают всегда, когда требуется по части охарактеризовать целое. Ошибка репрезентативности (m) является важнейшей статистической величиной, необходимой для оценки достоверности результатов исследования. По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном наблюдении, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования всех без исключения элементов генеральной совокупности. Определять величину ошибок репрезентативности следует только в тех случаях, когда организация исследования исключает все другие виды ошибок или когда все они сведены к минимуму.
12.Покажите и объясните пример по оценке генерального параметра по выборочному показателю.
Чтобы оценить генеральные параметры нужно: 1.установить число степеней свободы. 2.в соответствии с числом степени свободы найти значение критерий надежности (t) по таблице стандартных значений критерия Стьюдента. 3.рассчитать ошибку репрезентативности. 4. установить доверительные границы.
Например:изучены длина стебля у 100 растений и получены следующие выборочные показатели: n=100, Xср=130, t=2, σ=18
m= 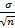 . Решение: m= 1,8 ; ∆=2*1,8=3,6
. Решение: m= 1,8 ; ∆=2*1,8=3,6
А(с черточкой волнистой вверху)-∆=130-3,6; А(с черточкой волнистой вверху)+∆=. А(с черточкой вверху)-генеральный параметр А=[( А(с черточкой волнистой вверху)-∆)+( А(с черточкой волнистой вверху)+∆) ]
Выборочные характеристики, как правило, не совпадают по абсолютной величине с соответствующими генеральными параметрами. Величину отклонения выборочного показателя от его генерального параметра называют статистической ошибкой или ошибкой репрезентативности. Статистические ошибки присущи только выборочным характеристикам, они возникают в процессе отбора вариант из генеральной совокупности.Ошибки репрезентативности необходимы для того чтобы выборочные показатели использовать для нахождения возможных значений генеральных параметров. По известным выборочным характеристикам можно построить интервал, в котором с той или иной вероятностью находится генеральный параметр. Это доверительные границы которые дают определить в каких пределах может находиться значения параметров.
13.Объясните понятия "достоверные" и "недостоверные" параметры. Опишите показатели точности и надежности.
Такие результаты выборочных исследований, по которым нельзя получить никакой определенной оценки генерального параметра (или он больше нуля, или меньше, или равен нулю), называются недостоверными. Следует твердо усвоить, что недостоверные результаты выборочного исследования не дают никакого определенного ответа. Очевидно, что достоверными результатами следует называть такие результаты выборочного исследования, которые совершенно определенно оценивают генеральный параметр. Показатель точности, или ошибка репрезентативности, выборочного показателя определяется на основе выборочных данных: m= 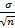 . По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном наблюдении, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования всех элементов генеральной совокупности. Судить о точности, с какой определена та или иная выборочная средняя, позволяет отношение ошибки репрезентативности к своей средней. P=m*100% / Хср. Точность вполне удовлетворительной, если коэффициент точности не превышает 3—5%. При Р больше 6, 7 % и более к полученным выводам следует отнестись очень осторожно и опыт повторить. Критерий надежности — это показатель вероятности безошибочных прогнозов. Так практика биологических работ выработала три основных порога вероятности безошибочных прогнозов: при обычной ответственности β1 = 0,95, при повышенной ответственности β2=О,99 и при высокой ответственности βз=0,999.
. По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном наблюдении, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования всех элементов генеральной совокупности. Судить о точности, с какой определена та или иная выборочная средняя, позволяет отношение ошибки репрезентативности к своей средней. P=m*100% / Хср. Точность вполне удовлетворительной, если коэффициент точности не превышает 3—5%. При Р больше 6, 7 % и более к полученным выводам следует отнестись очень осторожно и опыт повторить. Критерий надежности — это показатель вероятности безошибочных прогнозов. Так практика биологических работ выработала три основных порога вероятности безошибочных прогнозов: при обычной ответственности β1 = 0,95, при повышенной ответственности β2=О,99 и при высокой ответственности βз=0,999.
14.Опишите определение достоверности разности между средними арифметическими. Представьте пример использования мер достоверности.
В биостатистике всегда необходимо установить достоверность разности между средними двух групп. Для оценки достоверности разности между средними арифметическими двух выборочных совокупностей применяется критерий достоверности t-Стьюдента.
t-критерий Стьюдента используется для определения статистической значимости различий средних величин. Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:
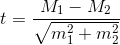
где М - средняя арифметическая сравниваемой совокупности, m - средняя ошибка средней арифметической.
Проверяется гипотеза: H0={Dx=Dy}. (нулевая гипотеза говорит о том, что различий нет)
- Если рассчитанное значение t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами.
- Если значение рассчитанного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы.
15.Опишите группировку вариант, отличающихся качественными признаками.
Довольно часто приходится иметь дело с различиями в совокупностях по качественным признакам, таким, как окраска мехового покрова животных или цветков растений, наличие или отсутствие различных морфологических признаков и т. д.

Приведен пример распределения 500 норок по окраске. Группировка сводилась к подсчету особей, относящихся к каждой качественной группе, и к выражениию количества особей каждой группы в виде относительной доли или просто доли в общем объеме совокупности. Эта доля может быть выражена или в процентах, или в долях единицы. Таким образом, при изучении качественных признаков мы встречаемся со следующими величинами: а) абсолютные численности группы — их обозначают символами ро, р1, р2 и т. д.; б) их доли, выраженные или в долях единицы, или в процентах(обозначения: q, р, r, s и т. д.). Частным случаем качественной вариации является альтернативная, когда в совокупности можно выделить только две группы. У членов одной группы присутствует определенное качество (или признак), у членов другой группы его нет. Так, при проверке на туберкулез животные распадаются на 2 группы—с положительной реакцией и с отрицательной.
(2-блок)
16.Приведите пример вычисления статистических показателей в сложных вариационных рядах по способу моментов.
Вариационный ряд – ряд, в котором сопоставлены (по степени возрастания или убывания) варианты и соответствующие им частоты. Статистические характеристики в сложных вариационных рядах гораздо легче рассчитывать упрощенным способом, называемым способом моментов. Применяется для обработки сложных вариационных рядов, при большом числе вариант. В данном случае условное среднее выбирается любой класс вариационного ряда и обозначается W и наз-ся центральное значение (которое находится путем сложения крайних вариант класса и деления на 2) Отклонение для каждого класса выставляется условно с учетом знаков + и -
̅х=W±b×L, b-поправка.
Например, в качестве примера было взято 40 растений с длиной стебля:
| X | f | A | fa | Fa2 |
| 100-113 | 5 | -2 | -10 | 20 |
| 114-126 | 9 | -1 | -9 | 9 |
| W=127-139 | 14 | 0 | 0 | 0 |
| 140-152 | 4 | 1 | 4 | 4 |
| 153-165 | 5 | 2 | 10 | 20 |
| 166-178 | 3 | 3 | 9 | 27 |
| Сумма=4 | Сумма=80 |
Рабочие формулы:
̅х=W±b×L, b-поправка. W - центральное значение.
σ= 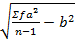 ×L
×L
b= 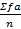
Решение: W= 127+139/2, L=13
b=0,1; ̅х=134,3; σ=18,57
Дата: 2019-05-28, просмотров: 537.