Простейшим показателем вариации является вариационный размах R, равный разности между наибольшим и наименьшим вариантами ряда – R = Х _max – Х _min .

Определение 4. Выборочной дисперсией S ² вариационного ряда называется среднее арифметическое квадрата отклонения вариантов от среднего арифметического –

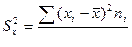.                                               (4)

Если ряд не сгруппированный, то дисперсия имеет вид

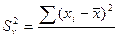.                                                (5)

На практике часто используется характеристика вариации, измеряемая в тех же единицах, что и признак – выборочное среднеквадратичное отклонение: .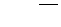

В некоторых случаях применяется безразмерная характеристика, так называемый коэффициент вариации                                               

V= 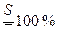.                                                    (6)

Свойства дисперсии

1. Выборочная дисперсия постоянной равна нулю, т.е. если х = с, то S ² _с = 0.

2. Если все варианты увеличить (уменьшить) в одно и тоже число k раз, то дисперсия увеличится в k ²  раз

S ² _кх = к² S ² _х.                                           (7)

3. Если все варианты увеличить (уменьшить) на одно и тоже значение, то дисперсия не изменится

S²_х+с = S²_х;                                                     (8)

.

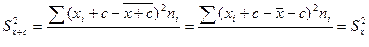4. Дисперсия равна разности между средней арифметической квадратов вариантов и квадратом средней арифметической

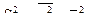;                                                       (9)

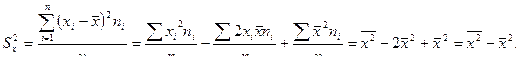
5. Если ряд состоит из нескольких групп наблюдений, то общая дисперсия равна сумме средней арифметической групповых дисперсий и межгрупповых дисперсий

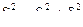,                                               (10)

где S_х² – дисперсия всего ряда,

S_g² = 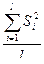 – средняя арифметическая групповых дисперсий,

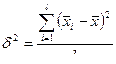 – межгрупповая дисперсия.

Другими характеристиками вариационного ряда являются начальные и центральные моменты k -го порядка, коэффициент асимметрии, эксцесса и т.д.

Заметим, что среднее арифметическое, дисперсия и другие характеристики вариационного ряда являются статистическими аналогами (оценками) математического ожидания, дисперсии и т.д.

Статистическая выборка

В статистике различают два вида наблюдений – сплошное, когда изучают все объекты совокупности, и выборочное, когда изучается часть объектов.

Примеры сплошных наблюдений: перепись населения, референдумы, медкомиссия призывников и т.д. Примеры выборочных наблюдений: социологические исследования, контроль качества, медицинские анализы, изучение флоры и фауны и т.д.

Определение 5. Вся совокупность объектов, подлежащих изучению, называется генеральной совокупностью. Дадим более строгое определение генеральной совокупности.

Определение 6. Генеральной совокупностью называется вероятностное пространство {Ω, S , P }и определенная на этом пространстве совокупность случайных величин Х (признаков).

Определение 7. Единицей (элементом) генеральной совокупности называется элементарное событие и отвечающее ему значение случайной величины Х (признака).

Определение 8. Часть объектов, которая отобрана из генеральной совокупности для изучения, называется выборкой (выборочной совокупностью).

Определение 9. Случайной выборкой объема n называется последовательность Х₁, Х₂,… Х _n n независимых, одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением исследуемой случайной величины Х.

Конкретный набор выборочных значений следует рассматривать как реализацию (одну из многих) многомерной случайной величины Х₁, Х₂, …, Х_n, компоненты которой независимы и имеют одну и ту же функцию распределения F(x), соответствующую генеральной совокупности.

Преимущества выборочного метода перед сплошным наблюдением:

– более экономичный в плане материальных затрат;

– единственно возможный в случае бесконечной генеральной совокупности или когда исследование сопровождается уничтожением наблюдаемых объектов.

Определение 10. Выборка называется репрезентативной, если она достаточно хорошо воспроизводит генеральную совокупность.

Различают следующие виды выборки:

– случайная выборка, состоящая в случайном выборе элементов совокупности;

– механическая выборка, в которую элементы из генеральной совокупности отбираются через определенные интервалы (например, каждый десятый);

– типическая (стратифицированная) выборка – генеральная совокупность разбивается на группы и в них делается выборка;