Если известна дисперсия случайной величины, то с ее помощью можно определить отклонение этой случайной величины на определенное значение от математического ожидания, причем оценка вероятности отклонения будет зависеть от дисперсии, а не от закона распределения. Получение такой оценки дает неравенство Чебышева, которое является частным случаем неравенства Маркова.
Теорема 1 (неравенство Маркова). Для любой случайной величины и любого t >0 (tÎR) вероятность события 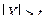 не превосходит частное от деления математического ожидания случайной величины на величину t
не превосходит частное от деления математического ожидания случайной величины на величину t
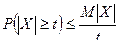 . (1)
. (1)
Доказательство. Докажем теорему отдельно для дискретного и непрерывного случая.
1. Пусть Х – дискретная случайная величина. Очевидно, что
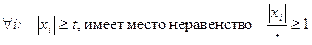 и
и 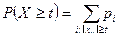 .
.
Тогда
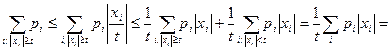
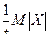 , следовательно
, следовательно
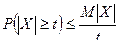 .
.
2. Пусть Х – непрерывная случайная величина, p(x) – плотность распределения вероятностей. Очевидно, что на промежутке (-¥, -t) и (t, +¥) 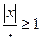 (так как
(так как 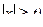 . Так как
. Так как
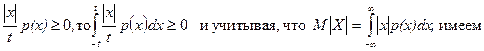
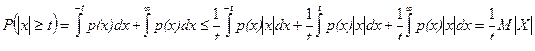 .
.
Неравенство Чебышева
Событие 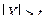 равносильно событию
равносильно событию 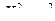 , оценим вероятность события
, оценим вероятность события 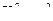 по неравенству Маркова, получим
по неравенству Маркова, получим
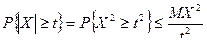 . (2)
. (2)
В неравенстве (2) заменим Х на Х – МХ, получим
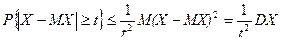 . (3)
. (3)
Неравенство (3) называется неравенством Чебышева. Оно справедливо для любых случайных чисел, имеющих конечную дисперсию. Замечательным свойством этого неравенства является то, что оценка не зависит от закона распределения случайной величины. Но при известном законе распределения можно получить более точную оценку. Например, пусть t = 3s, тогда по неравенству (3) имеем
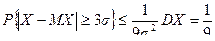 .
.
т.е. вероятность отклонения любой случайной величины от математического ожидания на величину, большую 3s, не более 1/9. Для нормального распределения легко получить более точную оценку – 0,0027.
Следствие 1. Для любых t > 0
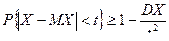 . (4)
. (4)
Доказательство. 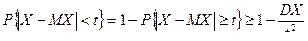 .
.
Для биномиального распределения неравенство (4) примет вид 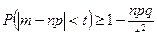 .
.
Следствие 2. Если Х1, Х2, …Хn – независимые случайные величины, то
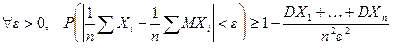 . (5)
. (5)
Смысл указанного неравенства оно дает оценку вероятности отклонения среднего арифметического случайных величин от среднего арифметического их математических ожиданий.
Доказательство. Пусть Y – случайная величина, 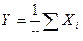 , тогда
, тогда 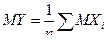 ,
, 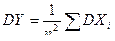 . Воспользуемся неравенством (17.4), заменив t на e, получим
. Воспользуемся неравенством (17.4), заменив t на e, получим
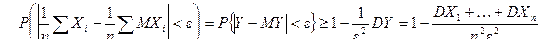 . (6)
. (6)
Закон больших чисел
Закон больших чисел устанавливает условия сходимости среднего арифметического случайных величин к среднему арифметическому математических ожиданий.
Определение 1. Последовательность случайных величин 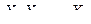 называется сходящейся по вероятности p к числу b, если
называется сходящейся по вероятности p к числу b, если
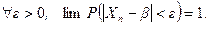
Сходимость по вероятности коротко обозначают так: 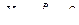 .
.
Теорема 2. (Закон больших чисел в форме Чебышева) Пусть 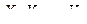 – последовательность независимых случайных величин, дисперсии которых равномерно ограничены сверху, т.е.
– последовательность независимых случайных величин, дисперсии которых равномерно ограничены сверху, т.е. 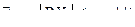 ; математические ожидания конечны, тогда
; математические ожидания конечны, тогда


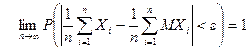 .
.
Доказательство. Так как DXi £ c, i = 1, 2, …, n, то 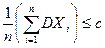 . Используя формулу (5) (следствие 2), имеем
. Используя формулу (5) (следствие 2), имеем
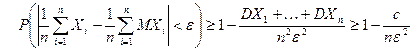 .
.
Так как вероятность любого события не превышает единицы, получим двойное неравенство
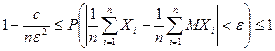 .
.
Перейдем в этом неравенстве к пределу при 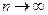 и получим
и получим
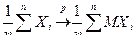 .
.
Дата: 2019-05-28, просмотров: 330.