В основе применения выводов и рекомендаций с помощью теории вероятностей и математической статистики лежит так называемый принцип практической уверенности.
Если вероятность события А в данном испытании очень мала, то при однократном выполнении испытания можно быть уверенным, что событие А не произойдет и в практической деятельности вести себя как будто событие А не произойдет.
Этот принцип не может быть доказан математически, но он подтверждается всем практическим опытом человеческой деятельности, и мы постоянно им руководствуемся (поездка на автомобиле, поезде, полет на самолете, сбор и употребление грибов, ограбление, заболевание и т.д.). Однако этот принцип справедлив при однократном выполнении испытания. Если произведено много испытаний, то существенно повышается вероятность того, что событие произойдет хотя бы один раз во всей совокупности испытаний.
Действительно, пусть вероятность наступления события А равна a, т.е. Р(А) = α, причем α значительно меньше единицы. Тогда из теории вероятностей известно, что вероятность того, что в серии из n независимых испытаний событие А произойдет хотя бы один раз равна
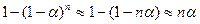 ,
,
т.е. вероятность наступления события А возросла в n раз.
Вопрос о том, насколько мала должна быть вероятность α события А, чтобы его можно было считать практически невозможным, решается в каждом отдельном случае с учетом важности последствий, вытекающих из наступления события А. В одних случаях можно пренебречь событиями, имеющими вероятность меньше 0,05 (финансовые операции, лечение больных, азартные игры и т.д.), а в других нельзя пренебречь событиями, которые могут произойти с вероятностью меньшей 0,001 (гибель людей, сооружений, значимых объектов и т.д.).
Непосредственное отношение к принципу практической уверенности имеет статистическая проверка гипотез. Статистическая проверка гипотез используется в различных областях человеческой деятельности, когда необходимо обосновать вывод о соответствии или преимуществах одних объектов, технологий перед другим. Например, при сравнении различных лекарственных препаратов по эффективности – в медицине; способов инвестиций – в финансовой деятельности; методик обучения – в педагогике и т.д.
Определение 1. Статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения, о соотношениях между параметрами различных групп случайных величин.
Проверяемую гипотезу обычно называют нулевой и обозначают H 0. Наряду с нулевой гипотезой рассматривают альтернативную, или конкурирующую, гипотезу H 1, являющуюся логическим отрицанием H 0. Эти гипотезы представляют собой две возможности выбора в задачах статистической проверки гипотез. Проверка статистических гипотез состоит в том, что используется специально составленная выборочная характеристика Θn(х1, х2,… х n), полученная по выборке Х1, …, Хn, закон распределения которой известен. По этому распределению определяется критическое значение Θкр – такое, что если гипотеза H 0 верна, то вероятность
Р(Θп>Θкр) = α
– бесконечно малая, почему в соответствии с принципом практической уверенности событие Θп>Θкр можно считать практически невозможным. Поэтому если в данном конкретном исследовании оказалось, что Θп>Θкр , то гипотеза Но отвергается. В то же время, если Θп<Θкр, то гипотезу принимаем. Правило, по которому гипотеза отвергается или принимается, называется критерием статистической проверки гипотез.
Таким образом, множество возможных значений статистики критерия Θn разбивается на два непересекающихся подмножества: критическую область (область отклонения гипотезы) W и область допустимых значений (область принятия гипотезы) 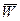 (рис.1).
(рис.1).
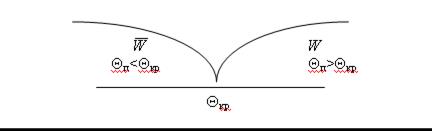
Рис. 1
При этом возможны четыре случая, которые приведены в таблице.
| Но | Принимается | Отвергается |
| Верна | Правильное решение | Неправильное решение, ошибка 1-го рода |
| Не верна | Ошибка 2-го рода | Правильное решение |
Определение 2. Вероятность α совершить ошибку 1-го рода, т.е. отвергнуть гипотезу H 0, когда она верна, называется уровнем значимости критерия.
Вероятность допустить ошибку второго рода, т.е. принять гипотезу H0, когда она неверна, обозначают β.
Определение 3. Вероятность 1 – β не допустить ошибку 2-го рода, т.е. отвергнуть гипотезу, когда она не верна, называется мощностью критерия.
Пользуясь терминологией статистического контроля качества продукции, можно сказать, что вероятность α – это «риск поставщика», связанный с забраковкой по результатам выборочного контроля изделий всей партии, на самом деле удовлетворяющей стандарту, а вероятность β – это «риск потребителя», связанный с принятием по анализу выборки партии, на самом деле, не удовлетворяющей стандарту.
Пользуясь юридической терминологией, α – это вероятность вынесения судом обвинительного приговора, когда на самом деле обвиняемый прав, а β – это вероятность вынесения судом оправдательного приговора, когда на самом деле обвиняемый виновен в совершении преступления.
Вероятности ошибок 1-го и 2-го рода (α, β) однозначно определяются выбором критической области. Очевидно желательно сделать сколь угодно малыми α и β. Однако при фиксированном объеме выборки можно сделать малой лишь одну из величин, что сопряжено с неизбежным увеличением другой. Лишь при увеличении объема выборки возможно одновременное уменьшение вероятностей α и β.
Заметим, что принцип проверки статистических гипотез не дает логического доказательства ее верности и неверности. Принятие гипотезы H0 в сравнении с альтернативной H1 не означает, что мы уверены в абсолютной правильности H0. Просто гипотеза H0 не противоречит имеющимся у нас выборочным данным.
Рассмотрим, как строится критическая область W [5]. Предположим, что используемая для проверки гипотезы H0 статистика критерия Θn имеет нормальный закон распределения N(a 0,s2). Тогда в качестве критической области, отвечающей уровню значимости α = 0,05, можно взять различные области, лишь бы площадь соответствующих им криволинейных трапеций под кривой распределения составляла 5% от общей площади. Например, это могут быть (рис. 2):
1 – область больших положительных отклонений (при Θn > Θкр1);
2 – область больших отрицательных отклонений (при Θn < Θкр2);
3 – область больших по абсолютной величине отклонений (при |Θn| > Θкр3);
4 – область малых по абсолютной величине отклонений (при |Θn| < Θкр4).
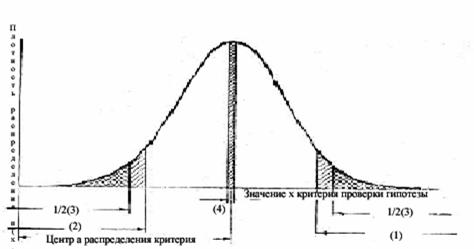
Рис. 2
Вопрос в том, какую из этих критических областей следует выбрать. Предположим, что с проверяемой гипотезой H0 конкурирует другая, альтернативная, гипотеза H1, при которой распределение статистики критерия Θn нормально – N(a1,s2). Причем а1 > a0. Если α зафиксировано и равно 0,05, очевидно, нужно выбрать ту критическую область, которой соответствует наибольшая мощность критерия 1–b, т.е. наибольшая вероятность того, что неверная (альтернативная) гипотеза будет отвергнута. Предположим мы выбрали критическую область 1, тогда, если Θn > Θкр1, гипотеза H0 принимается. Но в этом случае может быть верна конкурирующая гипотеза H1 с вероятностью ошибки второго рода b. При этом b на чертеже (рис. 3) интерпретируется как площадь под кривой 2 левее Θкр1, а мощность критерия 1-b – площадью Р1 правее Θкр1. Аналогично, Р2, Р3, Р4 соответствуют мощностям критерия при критических областях 2, 3, 4-го типов. Из графиков видно, что целесообразно выбрать критическую область 1, так как Р1 имеет наибольшее значение по сравнению с Р2, Р3, Р4 – при сдвиге кривой 1 вправо, она единственная из всех площадей увеличилась.
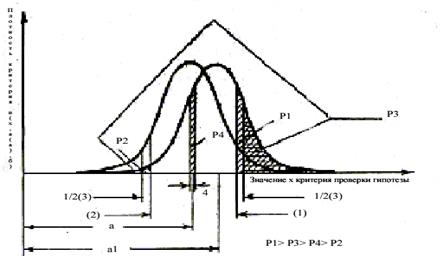
Рис.3
Таким образом, критическая область должна быть такой, чтобы при заданном уровне значимости α, мощность критерия 1– b была наибольшей. Задача построения такой критической области решается с помощью теоремы Неймана–Пирсона, излагаемой в более полных курсах математической статистики.
Дата: 2019-05-28, просмотров: 352.