Необходимость в использовании гипотез о равенстве дисперсий возникает часто, так как дисперсии характеризуют такие показатели, как точность измерительных приборов, технологических процессов, кучность стрельбы, риск экономических или финансовых операций и т.д.
Рассмотрим процедуру сравнения дисперсий в двух совокупностях с нормально распределенными признаками. Пусть дисперсии двух нормально распределенных совокупностей равны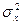 
и 
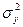. Необходимо проверить нулевую гипотезу о равенстве дисперсий –
Но: 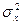= 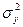(3)
Для проверки гипотезы (3) из этих совокупностей взяты выборки объема n1 и n2, По выборкам посчитаны выборочные дисперсии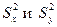 
. В качестве статистики используется величина F = 
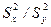(в числителе ставится бòльшая). Известно, что F имеет распределения Фишера с k1 = n1–1, k2 = n2 –1 степенями свободы.
Если F > F кр = Fa,k1,k2, то Но отвергается, в противном случае гипотеза принимается.
Рассмотрим процедуру сравнения дисперсий нескольких совокупностей с нормально распределенными признаками. Пусть имеется l нормально распределенных совокупностей, дисперсии которых равны соответственно s12 , s22, …,sl2 и l независимых выборок из каждой совокупности объемов n1, n2, …, nl. Нулевая гипотеза о равенстве дисперсий имеет вид
Но = s12 = s22 = …= sl2 = s2. (4)
Известно, что если гипотеза Но справедлива, то статистика c2, вычисленная по формуле (4) имеет распределение Пирсона с l –1 степенями свободы
c2 =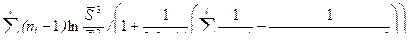 
,
где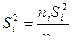 
– исправленная выборочная дисперсия l-й выборки;
.
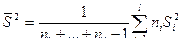Правило проверки состоятельности нулевой гипотезы следующее: если |t| > ta,k, то гипотеза Но отвергается; в противном случае – принимается, ta,k = t кр находят из соответствующей таблицы приложений.
Проверка гипотезы о законе распределения
Одной из важнейших задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по эмпирическому распределению. Для решения этой задачи необходимо определить вид и параметры закона распределения.
Предположение о виде закона распределения может быть выдвинуто исходя из теоретических предпосылок (например, выполняются условия центральной предельной теоремы); опыта аналогичных предшествующих измерений; на основании графического изображения (гистограммы) эмпирического распределения.
Параметры распределения, как правило, неизвестны, их заменяют наилучшими оценками по выборке.
Как бы хорошо не был подобран теоретический закон распределения, между эмпирическими и теоретическими законами распределения неизбежны расхождения. Возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и теоретический закон распределения подобран неудачно? Для ответа на этот вопрос и служат критерии согласия.
Пусть необходимо проверить нулевую гипотезу Но о том, что исследуемая случайная величина Х подчиняется определенному закону распределения. Для проверки гипотезы выбирают некоторую случайную величину U , характеризующую степень расхождения теоретического и эмпирического законов распределений. Закон распределения U при достаточно больших n известен и практически не зависит от закона распределения Х. Выбирают такое значение u, что если гипотеза Но верна, то P(U³u) = a мала.
Зная закон распределения U, можно найти вероятность того, что U приняла значение, не меньшее, чем фактически наблюдаемое в исследованиях, т.е. U³u. Если P(U³u) = a мала, то это в соответствии с принципом практической уверенности означает, что такие отклонения практически невозможны. В этом случае гипотезу Но отвергают. Если же вероятность P(U³u) = a не мала, расхождение между эмпирическим и теоретическим законом распределения не существенно и гипотезу Но можно считать правдоподобной и не противоречащей опытным данным.
В c2-критерии согласия Пирсона в качестве меры расхождения U берется величина c2, равная сумме квадратов отклонений частот wi от гипотетических p i, рассчитанных по предполагаемому распределению и взятых с некоторыми весами с i.
Определение 11. Кумулятивная кривая – это кривая накопленных частот.
На рис.3 приведена кумулятивная кривая оценок студентов по «Теории вероятностей и математической статистике».
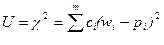. (5)
Веса сi вводятся таким образом, чтобы при одних и тех же отклонениях (wi – pi)2 больший вес имели отклонения, при которых pi мала, и меньший – при которых pi велика. Поэтому в качестве весов берут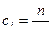 
.
Известно, что при n®¥, U, вычисленное по формуле 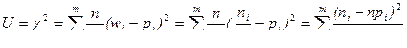(6),
(6)
имеет c2-распределение с k = m – r – 1 степенями свободы, где m – число интервалов эмпирического распределения (вариант ряда); r – число параметров теоретического распределения, вычисленных по эмпирическим данным.
Числа ni = nwi и npi называют соответственно эмпирическими и теоретическими частотами.
Алгоритм применения критерия c2 следующий:
1. Определяется мера расхождения эмпирических и теоретических частот c2.
2. Для выбранного уровня значимости a по таблице c2-распределения находят критическое значение c2a,к при числе степеней свободы k = m – r – 1.
3. Если c2 > c2a,к , то гипотезу Но отвергаем, в противном случае – принимаем.
ЛЕКЦИЯ 25. ЭЛЕМЕНТЫ РЕГРЕССИОННОГО И КОРРЕЛЯЦИОННОГО АНАЛИЗОВ
К наиболее простым зависимостям тапа Y = f(X) (такие зависимости в литературе еще называют парными) относится подавляющее большинство формул, используемых в естественнонаучных и технических дисциплинах. Такие формулы, как правило, строятся по результатам экспериментов, применяя метод наименьших квадратов. Однако только сейчас с использованием вычислительной техники стало возможным строить парные зависимости оптимальной (в смысле адекватности) формы.
Пусть имеется n пар наблюдений значений зависимой переменной yi – функции отклика, полученных при фиксированных значениях независимой переменной xi – фактора.
| xi | x1 | x2 | … | xn |
| yi | y1 | y2 | … | yn |
Пары (xi , yi) на плоскости можно представить в виде точек с координатами (xi , yi) (рис.1).
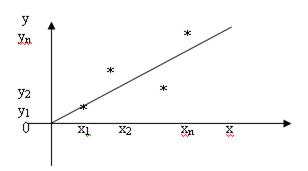
Рис.1
Задача регрессионного анализа состоит в том, чтобы, зная положение точек на плоскости, так провести линию регрессии, чтобы сумма квадратов отклонений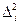 
вдоль оси 0Y этих точек от проведенной линии была минимальной. Для проведения регрессионного анализа к выдвигаемой гипотезе (к форме уравнения регрессии) выдвигается требование, чтобы это уравнение было линейным по параметрам или допускало линеаризацию. Рассмотрим сначала процедуру построения линейной зависимости между фактором и откликом.
Уравнение прямой линии на плоскости имеет вид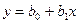 
, где 
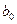и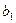 
– неизвестные постоянные. Тогда задачу метода наименьших квадратов можно сформулировать следующим образом – минимизировать функционал U по параметрам 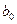и
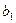
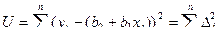. (1)
Решение задачи сводится к вычислению значений параметров 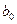и 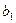, доставляющих функционалу (1) минимальное значение. Необходимое условие экстремума запишем в виде системы 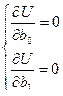(2)
. (2)
После нахождения производных получим так называемую систему нормальных уравнений 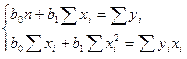(3)
. (3)
Для нахождения решения системы можно воспользоваться соотношениями (4)
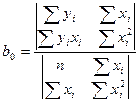и 
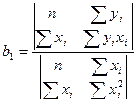. (4)
В общем случае между X и Y может быть два вида связи – функциональная и стохастическая. Первая имеет место, если точки наблюдения эксперимента расположены точно на линии регрессии. При наличии погрешностей измерения – связь стохастическая. Для функциональной связи понятие корреляции r не имеет смысла (коэффициент корреляции равен 1 при линейной зависимости). Для стохастической связи вычисление корреляции между X и Y и его оценка – важная статистическая процедура, которая позволяет судить о тесноте связи между X и Y. Коэффициент корреляции r может изменяться от –1 до +1. Чем ближе r к единице, тем связь между откликом и фактором теснее. Если X и Y имеют нормальное распределение, то равенство r нулю означает независимость X и Y. X и Y имеют две линии регрессии. Одна определяет зависимость Y от X, а вторая – зависимость X от Y. Прямые регрессии пересекаются в «центре тяжести» (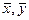 
) и образуют «ножницы». Чем уже «ножницы», тем ближе стохастическая связь к функциональной. Это означает, что уравнение регрессии 
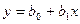не является алгебраическим, из которого можно выразить X через Y.
Коэффициент парной корреляции можно определить по формуле (5)
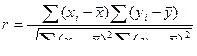, (5)
где 
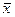и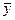 
– выборочные средние.
После определения коэффициентов уравнения регрессии и коэффициента корреляции необходимо оценить их статистическую значимость.
Статистическую значимость уравнения регрессии определяют с использованием критерия Фишера. Вычисляют статистику F-критерия по следующему соотношению 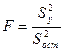(6):
, (6)
где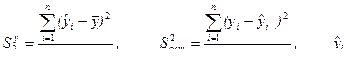 
.
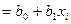Далее по таблице приложения находят табличное значение F-критерия при уровне значимости a и степенями свободы n – 1, n – 2.
Если F < F(a, n – 1, n – 2), то это означает, что уравнение регрессии статистически незначимо и неадекватно описывает результаты эксперимента; в противном случае уравнение регрессии статистически значимо. F-критерий показывает во сколько раз уравнение регрессии предсказывает результаты экспериментов лучше, чем среднее .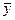
Для оценки статистической значимости r используется критерий Стьюдента:
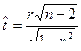(7)
Вычисленное по формуле (7)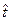 
сравнивают с табличным – t(n – 2, a), если 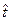> t(n – 2, a), то нуль гипотезу H0: r = 0 отклоняют, т.е. найденное r статистически значимо отличается от нуля.
Статистическую значимость коэффициентов регресси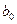и и 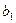также определяют при помощи критерия Стьюдента.
Адекватность модели можно оценить также при помощи коэффициента детерминации:
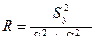. (8)
Чем ближе значение R к единице, тем адекватнее уравнение регрессии описывает исследуемый процесс.
Линеаризующие преобразования
В случае неадекватности линейного уравнения регрессии можно построить уравнение нелинейной регрессии, например, полиномиальной регрессии второй или третьей степени. При этом аналогично изложенному ранее, методом наименьших квадратов можно найти коэффициенты для квадратичной и кубической регрессий –
; 
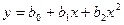. (9)
В некоторых случаях можно значительно упростить процедуру построения нелинейной модели, применив линеаризацию по параметрам или по переменным модели.
Например, установлено, что в задаче слежения за целями уровень возбуждения объектов и их производительность связаны следующей квадратичной зависимостью:
.
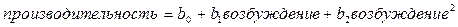Эта модель не линейна по переменным, но линейна по параметрам. Если сделать замену
х1 = возбуждение; х2 = возбуждение2,
то получим линейное уравнение – y = b0 + b1x1 + b2x2.
Известно, что скорость роста человека с увеличением возраста изменяется по следующему экспоненциальному закону:
скорость роста = exp (- b 1 *возраст). (10)
Эта модель не линейна и по переменным и по параметрам, но допускает линеаризацию. Прологарифмируем это уравнение и сделаем замену ln ( c корость роста) = y, возраст = х, получим линейное уравнение у = -b1х.
В таблице приведены примеры нелинейных зависимостей и соответствующие им линеаризующие преобразования [6].
| Функция | Линеаризующие преобразования | |||
| y’ | x’ | b’0 | b’1 | |
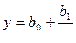
| y | 1/x | b0 | b1 |
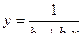
| 1/ y | х | b0 | b1 |
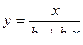
| x / y | х | b0 | b1 |
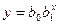
| lny | x | lnb0 | lnb1 |
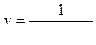
| 1/у | ехр(-х) | b0 | b1 |
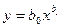
| lny | lnх | lnb0 | b1 |
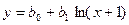
| у | ln(х+1) | b0 | b1 |
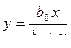
| 1/у | 1/x | b1/ b0 | 1/ b0 |
Дата: 2019-05-28, просмотров: 200.
