Между случайными величинами может существовать функциональная взаимосвязь. Однако связь может быть и такого рода, что закон распределения одной случайной величины изменяется в зависимости от значений, принимаемых другой случайной величиной. Такую зависимость называют стохастической или вероятностной. Одной из характеристик стохастической взаимосвязи двух случайных величин является ковариация случайных величин.
Определение 1. Ковариацией случайных величин Х i и Х j называется число, равное математическому ожиданию произведения отклонений случайных величин Х i и Xj от своих математических ожиданий
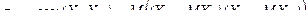 . (1)
. (1)
При вычислении используется формула
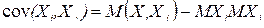 . (2)
. (2)
Покажем справедливость этого утверждения:
sij= M((Xi – MXj) (Xj – MXj)) = M(Х i Х j – Xi MXj – MXj Xj + MXj MXj) =M(Х i Х j) – MXj MXj – MXj MXj + MXj MXj = M(Х i Х j) – MXj MXj .
Если Х i и Х j независимы, то ковариация равна нулю, так как М(Х i , Xj) = МХ i М Xj. Обратное утверждение неверно. Если ковариация не равна нулю, то случайные величины зависимы.
Рассмотрим некоторые свойства ковариации:
1) cov(X, Y) = cov(Y, X);
2) cov(X, X) = DX;
3) cov(X + c, Y + c) = cov(X, Y);
4) cov(Xc1 + Yc2, Z) = с 1 cov(X, Z) + с 2 cov(Y, Z), с 1 , c2 – const.
Пусть задан случайный вектор X = (X1, X2,…, Xn).
Определение 2. Ковариационной матрицей случайного вектора X = ( X 1 , X 2,…, Xn ) назвается матрица å , элементами которой являются ковариации 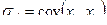 :
:
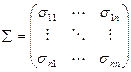 (3)
(3)
Очевидно, что матрица симметричная, а диагональные элементы равны дисперсиям случайных величин Хi, sii = DXi , i = 1,2,…
Определение 3. Определитель ковариационной матрицы å называется обобщенной дисперсией случайного вектора, который характеризует меру рассеивания случайного n -мерного вектора.
В теории вероятностей и её приложениях часто появляется необходимость перейти с помощью линейного преобразования к новым случайным величинам, X = (X1, X2, …, Xn)→ Y = (Y1, Y2, …,Ym), при этом 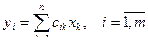 .
.
Обозначим через С = {cij} матрицу коэффициентов линейного преобразования, через Х и Y – векторы столбцы 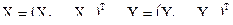 , тогда линейное преобразование можно записать как Y = CX .
, тогда линейное преобразование можно записать как Y = CX .
Теорема 1. Если для случайного вектора Х существует ковариационная матрица Σ, то при любых значениях элементов матрицы С существует ковариационная матрица Н для случайного вектора Y = CX, причём  .
.
Доказательство. Пусть 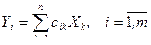 ;
; 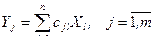 ;
;
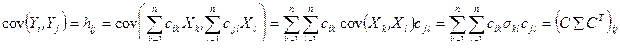 Следствие 1.
Следствие 1.
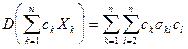 . (4)
. (4)
Доказательство. Пусть 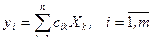 .
.
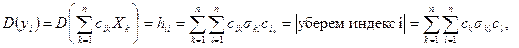
например, если n = 2, то 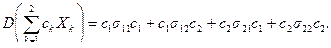
Следствие 2. Если в формуле из следствия 1 предположить, что 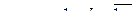 , то
, то
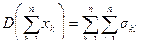 . (5)
. (5)
Следствие 3. Если в формуле из следствия 1 предположить, что n = 1, то
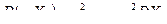 .
.
Следствие 4. Если в формуле из следствия 2 предположить, что n = 2, то
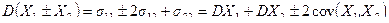 (6)
(6)
Следствие 5. Если Х k независимы, то в матрице å все недиагональные элементы равны нулю, а диагональные элементы равны дисперсиям соответствующих элементов Хк, поэтому, учитывая следствие 2, имеем
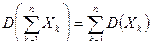 .
.
Пример 1. Вычислим ковариационную матрицу å случайного вектора Z = (X , Y), дисперсии случайных величин U1 = X+Y, U2 = 2X–3Y и ковариационную матрицу Н вектора U = (U1, U2). Распределение случайного вектора Z задано в таблице.
| J | 1 | 2 | 3 | 4 | pi· | |
| I |  Yj
Xi Yj
Xi
| 0 | 0,1 | 0,2 | 0,3 | |
| 1 | 5 | 0,2 | 0,1 | 0,05 | 0,05 | 0,4 |
| 2 | 6 | 0 | 0,15 | 0,15 | 0,15 | 0,1 |
| 3 | 7 | 0 | 0 | 0,1 | 0,1 | 0,2 |
| p·j | 0,2 | 0,25 | 0,3 | 0,25 | 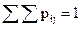
|
МХ = 5·0,4+6·0,4+7·0,2 = 5,8; М Y = 0·0,2+0,1·0,25+0,2·0,3+0,3·0,25 = 0,16;
М(Х ,Y)= 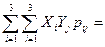 5·0·0,2+5·0,1·0,1+5·0,05·0,2+5·0,05·0,3+6·0·0+6·0,1·0,1+6·0,15·0,2+6·0,1·0,3+7·0·0+7·0·0,1+7·0,1·0,2+7·0,1·0,3 = 0,975.
5·0·0,2+5·0,1·0,1+5·0,05·0,2+5·0,05·0,3+6·0·0+6·0,1·0,1+6·0,15·0,2+6·0,1·0,3+7·0·0+7·0·0,1+7·0,1·0,2+7·0,1·0,3 = 0,975.
Матрица å имеет вид å= 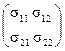 , где s11 = cov(X,X), s12 = cov(X,Y), s21 = cov(Y,X), s22 = cov(Y,Y);
, где s11 = cov(X,X), s12 = cov(X,Y), s21 = cov(Y,X), s22 = cov(Y,Y);
s12 = s21 = M(XY)-MXMY = 0,975-5,8·0,16 = 0,047;
s11 = cov(X,X) = DX=MX2 – (MX)2 = (52·0,4+62·0,4+72·0,2) – 5,82 = 0,56;
s22 = cov(Y,Y) = DY = MY2 – (MY)2 = (0·0,2+0,12·0,25+0,22·0,3+0,32·0,25) – 0,162 = 0,0114.
Следовательно, å = 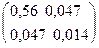 .
.
Найдем DU1 = D(X + Y)= 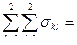 0,56 + 0,047 + 0,047 + 0,0114 = 0,6654;
0,56 + 0,047 + 0,047 + 0,0114 = 0,6654;
DU2 = D(2X – 3Y) = 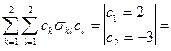 c1s11c1 + c1s12c2 + c2s21c1+ c2s22c2 = 2·2·0,56 – 2·3·0,047 – 3·2·0,047 + 3·3·0,0114 = 1,778.
c1s11c1 + c1s12c2 + c2s21c1+ c2s22c2 = 2·2·0,56 – 2·3·0,047 – 3·2·0,047 + 3·3·0,0114 = 1,778.
Ковариационную матрицу вектора U = (U1, U2) можно определить по формуле
 , где С =
, где С = 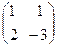 , тогда Н =
, тогда Н = 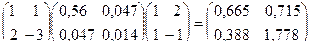 .
.
Из свойств ковариации следует, что значение ковариации линейно зависит от масштаба измерения случайных величин. Если изменить масштаб, то изменится и значение ковариации, например, если от случайной величины Х2 перейти к новой случайной величине Y2 = с2 Х2, то cov(X1, Y2) = c2cov(X1,X2). Это свойство ковариации ограничивает возможности его применения. Для получения характеристики взаимосвязи случайных величин, которая бы не зависела от преобразования случайных величин вида Y = а X + в, перейдем к рассмотрению нормированных случайных величин.
Пусть Х1, Х2 – случайные величины. Тогда им соответствуют нормированные величины: 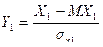 ,
, 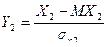 .
.
Найдем ковариацию Y1,Y2
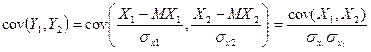 – коэффициент корреляции случайных величин.
– коэффициент корреляции случайных величин.
Определение 4. Коэффициентом корреляции случайных величин Х1, Х2 называется число r х1, х2 равное ковариации нормированных случайных величин Х1, Х2, т.е.
rх1, х2 = 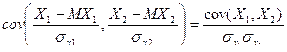 .
.
Для независимых случайных величин rх1,х2 = 0, так как cov(X1,X2) = 0. Обратное утверждение не верно (оно справедливо только для нормально распределенных случайных величин), но если rх1,х2 ¹ 0, то случайные величины Х1, Х2 – зависимы.
Определение 5. Случайные величины называются некоррелированными, если r х1, х2 = 0.
При изменении масштаба случайной величины значение корреляции не изменяется.
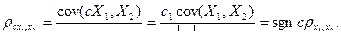
Рассмотрим пример, который показывает, что из равенства нулю коэффициента корреляции не следует независимость случайных величин.
Пусть 
 , тогда
, тогда
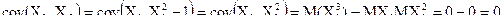
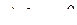 .
.
Теорема 2. Абсолютное значение коэффициента корреляции меньше либо равно 1: 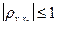 .
.
Доказательство. Пусть заданы случайные величины Х1, Х2. Рассмотрим нормированные случайные величины 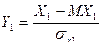 ,
, 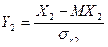 . Тогда в соответствии с формулой (6)
. Тогда в соответствии с формулой (6)
 следовательно,
следовательно, 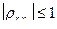 .
.
Теорема 3. 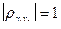 , тогда и только тогда, когда X1, X2 связаны линейной зависимостью, т.е. Х2 = aХ1 + b, причем если a > 0, то
, тогда и только тогда, когда X1, X2 связаны линейной зависимостью, т.е. Х2 = aХ1 + b, причем если a > 0, то 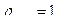 ; если a< 0, то
; если a< 0, то 
Доказательство.
I. Пусть 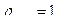 . Покажем, что Х1 и Х2 линейно зависимы.
. Покажем, что Х1 и Х2 линейно зависимы.
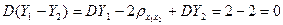 , т.е.
, т.е. 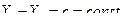
Покажем, что с = 0.
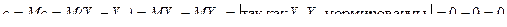 , т.е.
, т.е. 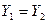 ,
,
следовательно 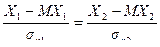 . Запишем последнее равенство в виде
. Запишем последнее равенство в виде
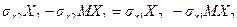 ,
,
выразим из него Х2:
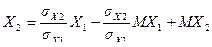 ,
,
обозначив множитель при первом слагаемом a, а два других через b, получим, что
Х2 = aХ1 + b.
Аналогичный результат можно получить в предположении, что 
II. Пусть Х2 = aХ1 + b, покажем, что 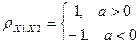 .
.
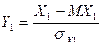 ,
, 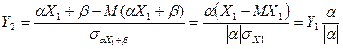 , следовательно
, следовательно
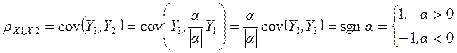
Дата: 2019-05-28, просмотров: 382.