Пусть Z = (X,Y) – двумерная случайная величина. Рассмотрим, как найти условное среднее случайной величины Z при условии, что Y = y. Предположим, что Z – дискретная случайная величина, p_ij = P(X = x_i, Y = y_j), 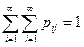. На предыдущих лекциях (лекция 8) нами было показано, что

; ,

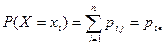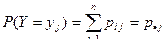и что условные вероятности

;

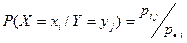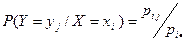
удовлетворяют условиям

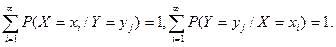
Поэтому при фиксированных у _j и х _i , вероятности P(X = x_i / Y = y_j), P(Y = y_j/X = x_i) можно рассматривать как условные распределения случайных величин Х (при условии, что Y = y_j) и Y (при условии, что Х = х _i). Тогда

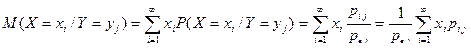
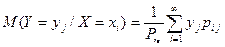
Предположим, что Z – непрерывная двумерная случайная величина, p_z (Х,Y) – плотность Z; p_x ( x ) – плотность X ; p_y ( y ) – плотность Y. Тогда условную плотность распределения Х при условии, что Y = y, определим

,

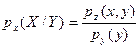а условную плотность распределения Y при условии, что Х = х, определим

.

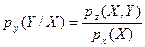Найдем условное математическое ожидание Х при условии, что Y = y в соответствии с формулой (2) предыдущей лекции

M(X/y) = M(X/Y = y)=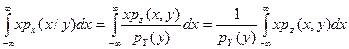

Аналогично,

.

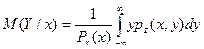Функция f_x(y) = М(Х/у) каждому у ставит в соответствие условное математическое ожидание Х при условии, что Y = y, т.е. она отражает зависимость от у условного среднего Х. Функция f_x(y) = М(Х/у) называется функцией регрессии Х на У.

Аналогично, функция f _у(х) = М(Y /x) называется функцией регрессии Y на Х.

Найдем математическое ожидание от математического ожидания М( X /у). Ограничимся рассмотрением дискретных случайных величин.

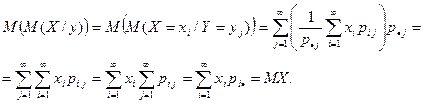
Таким образом, M(M(X/y)) = MX и называется формулой полного математического ожидания.

Другие характеристики центра группирования случайной величины

1.  Среднегеометрическое случайной величины Х: G(Х) = e^{M(ln Х)}.

Пусть Х – дискретная случайная величина, имеющая равномерное распределение.

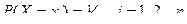, тогда

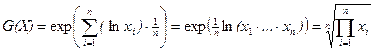– среднее геометрическое.

2. Среднее гармоническое: .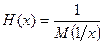

Используется в экономике в индексных расчетах.

3. Медиана: M_e(x) – квантиль x_p, соответствующая вероятности p = 0,5.

Точка х_р, являющаяся решением уравнения F ( x_p ) = р, называется квантилью распределения. Медиана используется в качестве характеристики среднего, если случайная величина измерена в порядковой шкале.

4. Мода: M ₀ ( x ) – это значение случайной величины, соответствующей максимальной вероятности p_i , если X – дискретная величина. Используется для оценки среднего величин, измеренных в номинальной шкале.

Если Х – непрерывная случайная величина, то мода – точка локального максимума плотности распределения.

Если плотность одномодального распределения непрерывной случайной величины симметрична относительно некоторой прямой х = а, то МХ = М_е(х) = М₀(х) = а.