Определение. Случайные величины Х₁, Х₂, …, Х _n называются независимыми, если для любых x _1, x ₂ , …, x_n независимы события

{ω: Х₁(ω) < x },{ω: Х₂(ω) < x },…, {ω: Х _n (ω) < x_n }.

Из определения непосредственно следует, что для независимых случайных величин Х₁, Х₂, …, Х _n функция распределения n-мерной случайной величины Х = Х₁, Х₂, …, Х _n равна произведению функций распределения случайных величин Х₁, Х₂, …, Х _n

                          F(x_1, x₂, …, x_n) = F(x₁)F(x₂)…F(x_n).                                     (1)

Продифференцируем равенство (1) n раз по x _1, x ₂, …, x_n,  получим

                           p(x_1, x₂, …, x_n) = p(x₁)p(x₂)…p(x_n).                                 (2)

Можно дать другое определение независимости случайных величин.

Если закон распределения одной случайной величины не зависит от того, какие возможные значения приняли другие случайные величины, то такие случайные величины называются независимыми в совокупности.

Например, приобретены два лотерейных билета различных выпусков. Пусть Х – размер выигрыша на первый билет, Y – размер выигрыша на второй билет. Случайные величины Х и Y – независимые, так как выигрыш одного билета никак не повлияет на закон распределения другого. Но если билеты одного выпуска, то Х и Y – зависимые.

Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина.

Теорема 1 (свёртки) или «теорема о плотности суммы 2 случайных величин».

Пусть X = (Х₁;Х₂) – независимая непрерывная двумерная случайная величина, Y = Х₁ + Х₂. Тогда плотность распределения

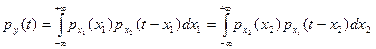                    .        (3)

Доказательство. Можно показать, что если 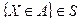, то

,

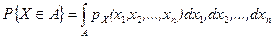где Х = (Х₁, Х₂, …, Х _n). Тогда, если Х = (Х₁, Х₂), то функцию распределения Y = X₁ + X₂ можно определить так (рис. 1) –

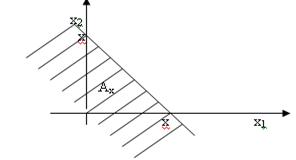
Рис. 1

= .

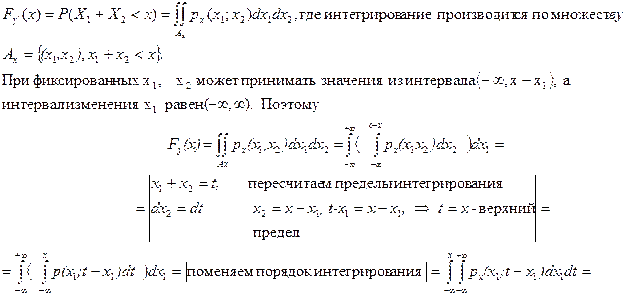
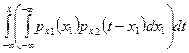В соответствии с определением, функция 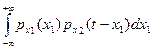 является плотностью распределения случайной величины Y = X₁ + X₂, т.е.

                                   p_y (t) = 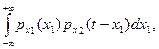 что и требовалось доказать.

Выведем формулу для нахождения распределения вероятностей суммы двух независимых дискретных случайных величин.

Теорема 2. Пусть Х₁, Х₂ – независимые дискретные случайные величины,

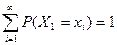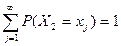, , тогда

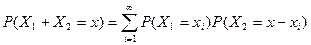                          .                       (4)

Доказательство. Представим событие A_x = {Х₁+Х₂ = x} в виде суммы несовместимых событий

A_x = å(Х₁ = x_i; Х₂ = x – x_i).

Так как Х₁, Х₂ – независимые то P(Х₁ = x_i; Х₂ = x – x_i) = P(Х₁ = x_i) P(Х₂ = x – x_i), тогда

P(A_x) = P(å(Х₁ = x_i; Х₂ = x – x_i)) = å(P(Х₁ = x_i) P(Х₂ = x – x_i)),

что и требовалось доказать.

Пример 1. Пусть Х₁, Х₂ – независимые случайные величины, имеющие нормальное распределение с параметрами N(0;1); Х₁, Х₂ ~ N(0;1).

Найдём плотность распределения их суммы (обозначим Х₁ = x, Y = X₁+X₂)

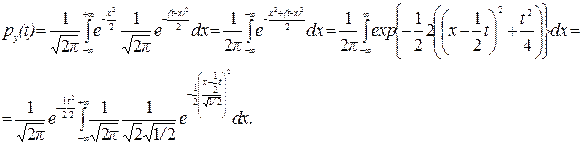
Легко видеть, что подинтегральная функция является плотностью распределения нормальной случайной величины с параметрами а = 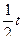, , 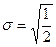т.е. интеграл равен 1.

Тогда

                         .

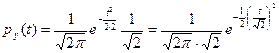Функция p_y (t) является плотностью нормального распределения с параметрами а = 0, s = . Таким образом сумма независимых нормальных случайных величин с параметрами (0,1) имеет нормальное распределение с параметрами (0, 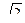), т.е. Y = Х₁ + Х₂ ~ N(0; ).

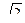Пример 2. Пусть заданы две дискретные независимые случайные величины, имеющие распределение Пуассона 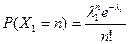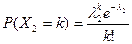, тогда       

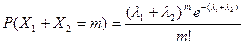                            ,                                              (5)

 где k , m , n = 0, 1, 2, …, ¥ .

По теореме 2 имеем:                 

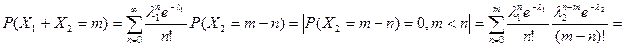
Пример 3. Пусть Х_1, Х₂ – независимые случайные величины, имеющие экспоненциальное распределение 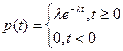. Найдём плотность Y= Х₁+Х₂.

Обозначим x = x_1. Так как Х_1, Х₂ – независимые случайные величины, то воспользуемся «теоремой свертки»

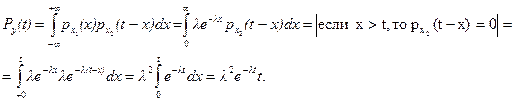
Можно показать, что если задана сумма 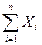 (Х _i  имеют экспоненциальное распределение с параметром l), то Y=  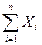имеет распределение 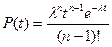, которое называется распределением Эрланга (n – 1) порядка. Этот закон был получен при моделировании работы телефонных станций в первых работах по теории массового обслуживания.

В математической статистике часто используют законы распределения случайных величин, являющихся функциями независимых нормальных случайных величин. Рассмотрим три закона наиболее часто встречающихся при моделировании случайных явлений.        

Теорема 3. Если независимы случайные величины Х_1, ..., Х _n, то независимы также функции от этих случайных величин Y₁ = f₁(Х₁), ...,Y_n = f_n(Х _n).

Распределение Пирсона (c²-распределение). Пусть Х_1, ..., Х _n – независимые нормальные случайные величины с параметрами а = 0, s = 1. Составим случайную величину

.

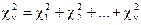Закон распределения случайной величины 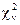 называется 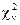-распределением (распределением Пирсона) с n степенями свободы.

Ранее нами была найдена плотность распределения квадрата нормальной случайной

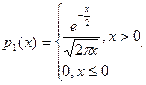
 Написанное выражение соответствует плотности распределения c² с числом степеней свободы n = 1. Получим плотность распределения при n = 2. Пусть 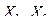– независимые нормально распределенные случайные величины: Х _i ~ N(0,1), i = 1,2. Так как Х₁, Х₂ независимы, то по теореме, сформулированной ранее независимы также .

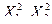Воспользуемся теоремой свёртки: n = 2, 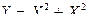, тогда для t > 0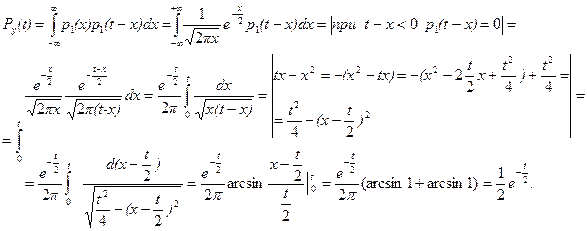

Таким образом,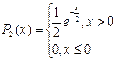                        

Можно показать, что плотность 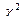 для х > 0 имеет вид 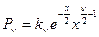, где k_n – некоторый коэффициент для выполнения условия 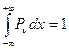. При n ® ¥ распределение Пирсона стремится к нормальному распределению.

Пусть Х₁, Х₂, …, Хn ~ N(a,s), тогда случайные величины 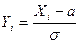 ~ N(0,1). Следовательно, случайная величина 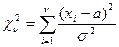имеет c² распределение с n степенями свободы.

Распределение Пирсона табулировано и используется в различных приложениях математической статистики (например, при проверке гипотезы о соответствии закона распределения).