Определение. Функцией распределения п-мерной случайной величины (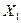 
, 
,…, 
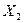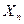) называется функция F(x 1 , x 2 , …, xn), определяющая вероятность совместного выполнения п неравенств X 1 < x 1 , X 2 < x 2 , …, Xn < xn , т.е.
F(x1, x2, …, xn) = P(X1 < x1, X2 < x2 , …, Xn < xn) (1)
В двумерном случае для случайной величины (X, У) функция распределения F(x,y) определится равенством:
F(x, y) = P(X < x, Y < y). (2)
Геометрически функция распределения F(x, y) означает вероятность попадания случайной точки (X, Y) в заштрихованную область – бесконечный квадрант, лежащий левее и ниже точки М(х, у) (рис. 1). Правая и верхняя границы области в квадрант не включаются – это означает, что функция распределения непрерывна слева по каждому из аргументов.
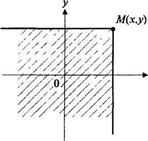
Рис.1
В случае дискретной двумерной случайной величины ее функция распределения определяется по формуле
F(x, y) = 
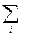
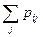, (3)
где суммирование вероятностей распространяется на все i, для которых xi < x, и все j , для которых у j < у.
Отметим свойства функции распределения двумерной случайной величины, аналогичные свойствам функции распределения одномерной случайной величины.
1. Функция распределения F ( x , у) есть неотрицательная функция, заключенная между нулем и единицей, т.е.
0 £ F(x,y) £1 (4)
2. Функция распределения F(x, у) есть неубывающая функция по каждому из аргументов, т.е.
при x2 > x1 F(x2,y) ³ F(x1,y), при y2 > y1 F(x,y2) ³ F(x,y1). (5)
Это свойство следует из того, что при увеличении какого-либо аргумента заштрихованная область на рис. 1 увеличивается, то вероятность попадания в него случайной точки (X, У), т.е. функция распределения F(x,y), уменьшиться не может.
2. Если хотя бы один из аргументов обращается в - ¥, функция распределения F(x, у) равна нулю, т.е.
F(x, – ¥,) = F(– ¥, y) = F(– ¥, – ¥) = 0 (6)
Функция распределения F(x, y) в отмеченных случаях равна нулю, так как события X < – ¥, Y < – ¥, и их произведение представляют невозможные события.
4. Если один из аргументов обращается в + ¥, функция распределения F(x, у) становится равной функции распределения случайной величины, соответствующей другому аргументу:
F(x, + ¥) = F1(x), F( + ¥, y) = F2(y), (7)
где F1(x) и F2(y) – функции распределения случайных величин X и Y, т.е.
F1(x) = P(X < x), F2(y) = P(Y < y).
Произведение события (X < x) и достоверного события (Y < + ¥) есть само событие (X < x), следовательно, F(x,+ ¥) = P(X < x) = F1(x). Аналогично можно показать, что
F(+ ¥, y) = F2(y).
5. Если оба аргумента равны + ¥, то функция распределения равна единице
F(+ ¥, + ¥) = 1.
Следует из того, что совместное осуществление достоверных событий (X < + ¥), (Y <+ ¥) есть событие достоверное.
Геометрически функция распределения есть некоторая поверхность, обладающая указанными свойствами. Для дискретной случайной двумерной величины (X,Y) ее функция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции F(x, у).
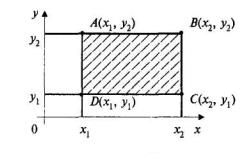
Рис. 2
Зная функцию распределения F(x, у), можно найти вероятность попадания случайной точки (X, Y) в пределы прямоугольника ABCD (рис. 2), т.е. P [ x1 £ X < x2, y1 £ Y <y2]. Так как эта вероятность равна вероятности попадания в бесконечный квадрант с вершиной B(x2, y2) минус вероятности попадания в квадранты с вершинами соответственно в точках A(x1, y2) и C(x2, y1) плюс вероятность попадания в квадрант с вершиной в точке D(x1, y1) (ибо эта вероятность вычиталась дважды), то
P[x1 £ X < x2, y1 £ Y < y2] = F(x2, y2) – F(x1, y2) – F(x2, y1) + F(x1, y1). (8)
Дата: 2019-05-28, просмотров: 224.
