Определение 3. Случайная величина X имеет геометрическое распределение, если
P(Х = m) = Pm = qm -1 p , m = 1, …
где q = 1– p , pÎ(0, 1). Геометрическое распределение имеет случайная величина X , равная числу испытаний по схеме Бернулли до первого наступления успеха с вероятностью успеха в единичном испытании р. Покажем, что Σpi = 1
.
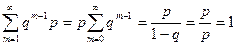Распределение Пуассона
Определение 4. Случайная величина Х имеет распределение Пуассона с параметром l, если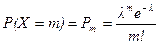 
, m = 0, 1, …
Покажем, что Σpm = 1.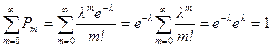 
.
Биномиальное распределение
Определение 5. Случайная величина X имеет биномиальное распределение, если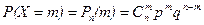 
, m = 0, 1, …, n,
где n – число испытаний по схеме Бернулли, m – число успехов, р – вероятность успеха в единичном исходе, q = 1– p.
Распределение Бернулли
Определение 6. Случайная величина Х имеет распределение Бернулли, если P(Х = m) = Pm = pmqn - m, m = 0, 1, …, n.
При больших m и n становится проблематичным вычисление по формуле Бернулли. Поэтому в ряде случаев удается заменить формулу Бернулли подходящей приближенной асимптотической формулой. Так если n – велико, а р мало, то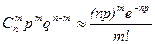 
.
Теорема Пуассона. Если n ® ¥, а p ® 0, так что np ® l, то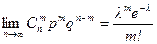 
.
Доказательство. Обозначим ln = np, по условию теоремы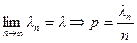 
, тогда
.
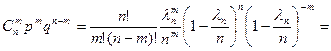
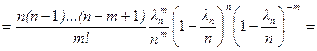
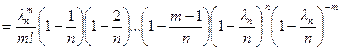При n ® ¥, ln m ® lm,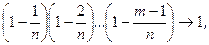 
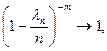
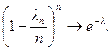
Отсюда получаем утверждение теоремы. Р n(m) ®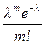 
при n ® ¥.
Формула Пуассона хорошо приближает формулу Бернулли, если npq £ 9. Если же произведение npq велико, то для вычисления Р n ( m ) используют локальную теорему Муавра–Лапласа.
Локальная теорема Муавра – Лапласа. Пусть pÎ(0;1) постоянно, величина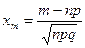 
равномерно ограничена, т.е. $с, | xm |<с. Тогда
,
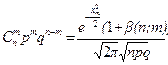где b ( n ; m ) – бесконечно малая величина, причем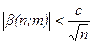 
.
Из условий теоремы следует, что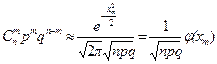 
,
где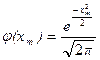 
, .
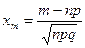Для вычисления Р n ( m ) по формуле, приведенной рнее, используют таблицы функции
.
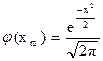Задача 1. В магазин одежды один за другим входят трое посетителей. По оценкам менеджера, вероятность того, что вошедший посетитель совершит покупку, равна 0,3. Составить ряд числа посетителей, совершивших покупку.
Решение .
| xi | 0 | 1 | 2 | 3 |
| рi | 0,343 | 0,441 | 0,189 | 0,027 |
Задача 2. Вероятность поломки произвольного компьютера равна 0,01. Построить ряд распределения числа вышедших из строя компьютеров с общим числом 25.
Решение .
| xi | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … | 25 |
| рi (Пуассон) | 0,778 | 0,196 | 0,024 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| рi (Бернулли) | 0,779 | 0,195 | 0,022 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
Задача 3. Автомобили поступают в торговый салон партиями по 10 шт. В салоне подвергаются контролю качества и безопасности только 5 из 10 поступивших автомобилей. Обычно 2 из 10 поступивших машин не удовлетворяют стандартам качества и безопасности. Чему равна вероятность, что хотя бы одна из 5 проверяемых машин будет забракована.
Решение. Р = Р(1) + Р(2) =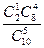 
+ 
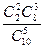=0,5556 + 0,2222 = 0,7778
Дата: 2019-05-28, просмотров: 254.
