Непрерывная случайная величина – это переменная, которая может принимать любое значение в одном или нескольких заданных интервалах или в некоторых областях плоскости. Дадим более строгое определение.

Определение 1. Случайная величина X – непрерывная случайная величина, если существует функция p ( x ) ³ 0, такая что, " x Î R , справедливо соотношение .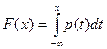

Ограничимся рассмотрением таких непрерывных случайных величин, для которых р(х) непрерывна всюду, кроме быть может, конечного числа точек.

Определение 2. Функция p (х) называется плотностью распределения вероятностей непрерывной случайной величины.

Свойства непрерывной случайной величины

1.                                                          .

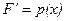Доказательство вытекает из определения.

2. Плотность распределения p ( x ) определяет закон распределения непрерывной случайной величины

.

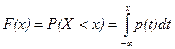Это свойство также следует из определения плотности р(х).

3. Для любых х₁ < х₂ ,   .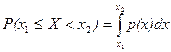

Доказательство. По свойству функции распределения .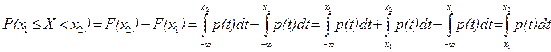

4.                                                 .

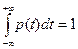Доказательство: .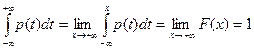

6. Вероятность того, что непрерывная случайная величина примет конкретное значение равна нулю, т.е.

                                              P(X = a) = 0.

Доказательство. Событие 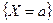 можно представить как 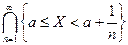. События A_n = 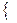a £ Х < a +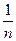 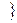удовлетворят условиям аксиомы непрерывности

A₁ É A₂ É…É A_n É…, .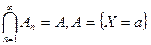

Тогда, применив аксиому, получим

.

Из этого свойства следует, что Р( a < X < b ) = P ( a ≤ X < b ) = P ( a < X ≤ b ) = P ( a ≤ X ≤ b ).

7. Если x – точка непрерывности p(x) и если Δ→0, то

.

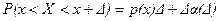Из этого свойства следует, что чем больше значение плотности p(x), тем больше вероятность попадания случайной величины в интервал (x; x + ∆).

Плотностью распределения может быть любая неотрицательная функция, интеграл от которой по всей числовой прямой равен 1, т.е. .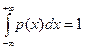

Функция распределения случайной величины любой точке x_p ставит в соответствие вероятность р = F(x_p) = P(X<x_p),  т.е. по x_p найти F(x_p). В иных случаях требуется решение обратной задачи ¾ по значению вероятности р найти решение уравнения F(x_p) = р.

Определение 3. Точка x_p , которая является решением записанного уравнения, называется квантилью, отвечающей заданному уровню вероятности р, или р % квантилью распределения F ( x ).

Из определения непрерывной случайной величины следует, что функция распределения непрерывной случайной величины непрерывна. Поэтому для непрерывной случайной величины для любого р, 0 < p < 1 существует квантиль х_р.

Определение 4. Квантиль, отвечающая вероятности р = ½, называется медианой распределения.

Медиана является одной из характеристик центра распределения случайных величин.

Законы распределения непрерывных случайных величин

Равномерное распределение

Определение 5. Непрерывная случайная величина Х, принимающая значение на отрезке [ a , b ], имеет равномерное распределение, если плотность распределения имеет вид

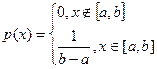                                            .                                        (1)

Нетрудно убедиться, что ,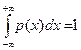

.

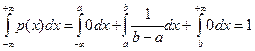Если случайная величина равномерно распределена, то вероятность того, что она примет значение из заданного интервала [x; x+∆] не зависит от положения интервала на числовой прямой и пропорциональна длине этого интервала

^.

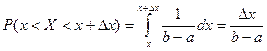Покажем, что функция распределения Х имеет вид

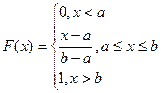                                     .                                           (2)

Пусть хÎ (–¥,a), тогда F(x) = .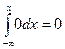

Пусть хÎ [a,b], тогда F(x) = .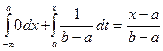

Пусть х Î (b,+¥], тогда F(x) = 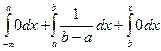 = 0 + .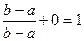

Найдем медиану x_0,5. Имеем F(x_0,5) = 0,5, следовательно

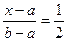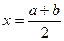, . Итак, медиана равномерного распределения совпадает с серединой отрезка [a, b]. На рис.1 приведен график плотности р(х) и функции распределения F(x)

для равномерного распределения.

Рис. 1