Для вычисления при больших n вероятности того, что число успехов в n испытаниях Бернулли находится между m ₁ и m ₂ , используется интегральная теорема Муавра–Лапласа.

Интегральная теорема Муавра – Лапласа. Если вероятность успеха в каждом испытании р, pÎ(0;1) постоянна, то при n ® ¥ для любых a , b     

.

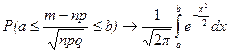На основании интегральной теоремы Муавра–Лапласа для вычисления вероятности события 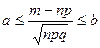 при больших n и npq >9 используют приближенную формулу

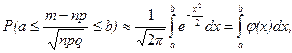
где .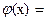

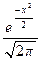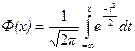Значения можно найти, воспользовавшись таблицами функции Лапласа , покажем это:   

= ,

т.е. при больших n ,

                               Ф( b ) – Ф(а).                   (1)

Значения функции Лапласа приведены в таблицах для х > 0. Для того, чтобы вычислить значения функции для отрицательных х, надо воспользоваться следующей теоремой.

Теорема. Ф( x ) + Ф(- x ) = 1.

Доказательство: j(x) – чётная, так как j(x) = j(-x). Тогда 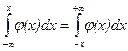 (рис.1).

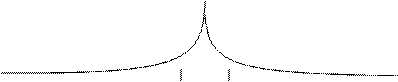                                            -х     х

Рис. 1

Следовательно, по интегральной теореме Муавра–Лапласа 

.

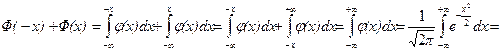
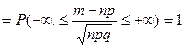В некоторых источниках Ф(х) определяется как .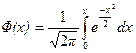

В этом случае                        Ф(–x) = –Ф(x).

Событие m ₁ £ m £ m ₂ эквивалентно событию .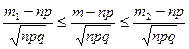

Поэтому, учитывая (1) для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено в пределах от m ₁ до  m ₂ , можно использовать формулу

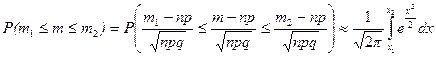   ,                 (2)

где , .

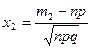Формула (2) хорошо работает, если n < 50. При больших значениях n лучше взять

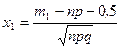 и .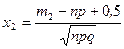

Обозначим через b вероятность того, что относительная частота наступления успеха в n испытаниях Бернулли отклонится от вероятности успеха p не более чем на e > 0, т.е. 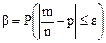. Покажем, что при достаточно больших n с помощью интегральной теоремы Муавра–Лапласа можно определить вероятность b.

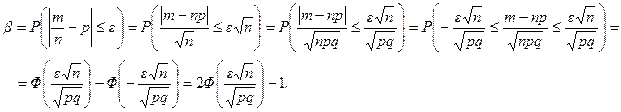
Следовательно, получим 

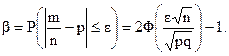                                                                        (3)

Формула содержит четыре параметра: n , p, e, b. Если известны любые 3, то можно определить четвертый параметр.

Если известны b, e, то n можно найти по формуле

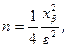                                                                                                    (4)

где 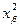– это квадрат числа х_b, такого, что Ф(х) = .

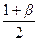Теорема Бернулли. Пусть m – число успехов в n испытаниях по схеме Бернулли, вероятность успеха в каждом испытании равна p, тогда

"e>0, .

Доказательство.

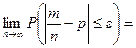
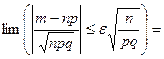
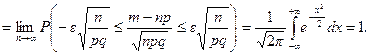
Задача 1. Вероятность того, что случайно выбранный прибор нуждается в дополнительной настройке, равна 0,05. Если при выборочной проверке партии приборов обнаруживается, что не менее 6 % отобранных приборов нуждаются в регулировке, то вся партия возвращается для доработки. Определить вероятность того, что партия будет возвращена, если для контроля из партии выбрано 500 приборов.

Решение . Партия будет возвращена, если число отобранных приборов, нуждающихся в настройке, будет больше 6%, т.е. m₁ = 500 × 6/100 = 30. Далее: p = 0,05: q = 0,95; np = 25; 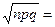4,87. За успех считаем, если прибор требует дополнительной настройки.

Применим интегральную теорему Муавра–Лапласа.

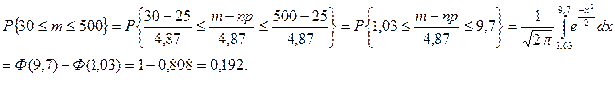
Задача 2. Определить, сколько надо отобрать изделий, чтобы с вероятностью 0,95 можно было утверждать, что относительная частота бракованных изделий будет отличаться от вероятности их появления не более чем на 0,01.

Решение . Для решения задачи выберем в качестве математической модели схему Бернулли и воспользуемся формулой (4). Надо найти такое n, чтобы выполнялось равенство (4), если e = 0,01, b = 0,95, вероятность р неизвестна.

Ф(х_b)  = (1 + 0,95) / 2 = 0,975. По таблице приложения найдем, что х_b = 1,96. Тогда по формуле (4) найдем n = ¼ × 1,96²/0,01² = 9600.