Развитие бескарданных (бесплатформенных) базовых систем отсчета стала вполне возможной после того прогресса вычислительной техники, который привел к появлению надежных бортовых цифровых вычислительных машин, обладающих нужным объемом памяти и достаточным быстродействием [15]. Это сделало возможным непрерывное интегрирование уравнений движения космического аппарата при сколь угодно сложном характере его движения, опираясь на показания, по сути, тех же датчиков первичной информации, что и используемые в платформах. Следовательно, в бесплатформенных системах громоздкие устройства подвеса со следящими приводами «заменяются» интегрированием уравнений движения [9, 15].

Типичная схема бесплатформенной системы управления космическим аппаратом показана на (рис 2.1). С бортовой цифровой вычислительной машиной 1 соединены три группы датчиков, условно обозначенных через Д₁,

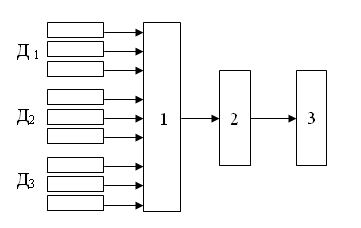
Рис 2.1 - Схема бесплатформенной системы управления ориентацией:

1 – бортовая цифровая вычислительная машина; 2 – блок согласования; 3-исполнительные органы

Д₂ и Д₃; вырабатываемые в машине сигналы управления преобразуются должным образом в блоке согласования   2, после чего поступают на исполнительные органы системы ориентации 3. Воздействуя на динамику космического аппарата (в зависимости от работы исполнительных органов, изменяется его угловое движение, и на входе вычислительной машины появляются измененные сигналы датчиков системы ориентации). На приведенной схеме все датчики условно разбиты на три группы в зависимости от основной задачи, выполняемой ими в полете.

Группа датчиков Д₁, по сути, обеспечивает существование на борту математической «платформы». Этими датчиками могут быть любые устройства, позволяющие регистрировать составляющие p, q и r угловой скорости космического аппарата, параллельные осям Ox, Oy и Oz жестко связанного с ним триэдра осей. Имея непрерывно измеряемые значения p(t), q(t), r(t), вычислительная машина интегрирует кинематические уравнения углового движения и непрерывно определяет соответствующие три угла поворота жестко связанного с корпусом космического аппарата триэдра осей Oxyz относительно некоторого условного, например, начального положения этого триэдра Ox’y’z’. Поскольку в результате вычислений положение триэдра Oxyz всегда известно для текущего момента времени с нужной точностью, постольку известно и расположение относительно корпуса космического аппарата начального триэдра Ox’y’z’. Таким образом, триэдр Ox’y’z’, положение которого относительно корпуса непрерывно вычисляется, может служить базовой системой отсчета углов для поступательно движущихся осей ориентации; в этом смысле тройка датчиков Д₁ и вычислительная машина заменяют гиростабилизированные платформы [1, 3, 9, 15].

Если необходимо иметь базовую систему отсчета для орбитальных осей ориентации при известной орбите космического аппарата, то бортовая вычислительная машина должна вычислять для каждого момента времени t, кроме уже сказанного, и положение орбитальных осей ориентации Ox”, Oy”, Oz” относительно поступательно движущихся осей Ox’, Oy’, Oz’ (эти вычисления никак не связаны с работой датчиков системы ориентации, в них используются данные об орбите космического аппарата и о взаимном положении осей Ox’, Oy’, Oz’ и Ox”, Oy”, Oz” в начальный момент времени t=0, которое предполагается известным). Поскольку в машине в этом случае есть все данные о взаимном положении триэдров Ox’y’z’ и Ox”y”z”, с одной стороны, и триэдров Oxyz и Ox’y’z’, с другой, то тем самым легко вычисляется и взаимное положение триэдров Oxyz и Ox”y”z”, т.е. углы ориентации для орбитальной системы осей [3]. В этом смысле тройка датчиков Д₁ и вычислительная машина, в память которой введены параметры заданной орбиты, заменяют платформу. Совершенно аналогично можно было бы вычислять в бортовой машине и углы ориентации для скоростной системы осей, поскольку их вращение в функции времени тоже определяется параметрами орбиты [1].

Приведенные примеры указывают на большую гибкость, которую сообщает управлению ориентацией использование бортовой вычислительной машины, - переход от управления относительно поступательно движущихся осей ориентации к управлению в орбитальных или скоростных осях может производиться практически мгновенно путем простого изменения программы работы машины [12, 15].

В качестве датчиков Д₁, о которых было сказано, что они являются любыми измерителями компонент угловых скоростей, могут быть использованы высокочастотные датчики угловых скоростей либо одноосные гиростабилизаторы, т.е. приборы, содержащие лишь один канал стабилизации углового положения платформы вместо трех. В рассматриваемом случае платформа не будет устанавливаться в кардановом подвесе, а будет иметь одну единственную ось вращения – ось Ox. Угол поворота платформы относительно корпуса космического аппарата вокруг этой оси обозначим через 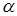. В таком случае компонента p’ угловой скорости вращения платформы по направлению Ox относительно абсолютного пространства будет равна 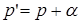. Если интегрирующий гироскоп и следящая система работают идеально, то  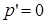и ,следовательно, 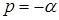, т.е. по темпу поворота платформы одноосного гиростабилизатора относительно корпуса космического аппарата можно судить о компоненте угловой скорости по соответствующей оси [9, 12].

Важно обратить внимание на то обстоятельство, что вращение вокруг одной оси может быть неограниченным, и поэтому недостатки, свойственные платформам в кардановых подвесах, отсутствуют [9]. Очевидно, что на борту космического аппарата надо иметь три таких одноосных гиростабилизатора с взаимно перпендикулярными осями чувствительности; образно выражаясь, для получения бескарданной базисной системы в этом случае надо «распилить» обычную гиростабилизированную платформу на три части и подсоединить их к вычислительной машине. В каком случае предпочтительно использовать датчики угловых скоростей и в каком - одноосные гиростабилизаторы – дело конкретной конструктивной проработки. Достаточно указать лишь на то, что в первом случае гироскопический элемент работает в измерительном режиме, во втором же случае – в режиме нуль-индикатора [21], что всегда проще для гироскопического элемента, хотя сам одноосный гиростабилизатор и сложнее датчика угловой скорости.

Бесплатформенные системы, использующие только набор датчиков Д₁, обладают тем же недостатком, что и некорректируемые гироплатформы, - вследствие уходов гироскопов их точность с течением времени падает. Чтобы избежать этого, к вычислительной машине подсоединяют датчики, обозначенные через Д₂  на рис.2.1. Это могут быть самые различные датчики внешней информации - построители местной вертикали, астродатчики и т.п [1, 12, 15]. По их сигналам вносятся поправки в вычисления, произведенные в машине на основе информации, получаемой с датчиков группы Д₁, и тем самым достигается независимость точности измерений углов ориентации от времени непрерывной работы. В некоторых режимах можно работать, основываясь на информации об углах ориентации, получаемой только с датчиков Д₂. В этих режимах датчики Д₁ могут играть роль простых датчиков угловых скоростей, если последние нужны для формирования сигналов управления. Возможны и другие комбинации использования подключенных к вычислительной машине датчиков: если, например, нужно реализовать режим орбитальной ориентации, то достаточно включить один датчик группы Д₂ – построитель местной вертикали, а по сигналам датчика Д₁ произвести курсовую ориентацию космического аппарата, используя их как инерциальные датчики ориентации. Количество датчиков Д₂ и их состав определяются задачами, стоящими перед космическим аппаратом [9, 12, 15, 21].

Приведенные примеры показывают большую гибкость системы управления ориентацией, использующей бесплатформенную базисную систему отсчета, не только в части управления угловым положением космического аппарата по отношению к разным осям ориентации, но и в том, что один и тот же режим ориентации может быть получен путем включения различных наборов датчиков.

Гиростабилизированные платформы применяются для обеспечения режимов управления движением центра масс и стабилизации углового положения при работе маршевых двигателей или управления спутником в атмосфере. Бесплатформенная система с использованием бортовой вычислительной машины способна обеспечить и такие режимы. С этой целью  к ней подключается группа датчиков, обозначенная через Д₃ (см. рис.2.1), например акселерометров [9, 15]. Хотя такие акселерометры стоят  неподвижно относительно корпуса космического аппарата и поэтому их оси чувствительности участвуют в поворотах вместе с корпусом, их показания для некоторого мгновения t всегда могут быть сопоставлены с углами ориентации относительно абсолютного пространства для того же t, получаемыми указанными выше способами. Это позволяет производить в машине соответствующие пересчеты и в конечном итоге путем интегрирования уравнений движения центра масс иметь все нужные данные для управления движением центра масс [1]. На рис. 2.1 связь бортовой                вычислительной машины с контуром управления движением центра масс и управления угловым положением при режимах, связанных с большими силовыми воздействиями на космический аппарат, не показана.

Бортовая вычислительная машина не только не делает управление гибким и вполне заменяет гироплатформу, но способна производить обработку сигналов, поступающих с датчиков внешней информации, с целью выделения полезного сигнала из шумов [7, 22]. Таким образом, во всех отношениях, в том числе и в способности работать фильтром для сигналов, характеризуемых заметными флуктуациями, бесплатформенная система вполне заменяет корректируемые гиростабилизированные платформы [12].

Применение бесплатформенных систем имеет большие перспективы, поскольку они не обладают недостатками платформ, установленных в кардановых подвесах [9, 12, 15].

2.2 Гироскопический измеритель вектора угловой скорости

Гироскопические системы ориентации позволяют получить необходимую информацию для автоматического управления ЛА автономными методами, без каких-либо иных, не зависящих от внешних помех источников информации (локация, радионавигация, астроориентация и др.) [1, 21].

Бесплатформенные (бескарданные) системы ориентации, чувствительными элементами которых являются гироскопические датчики первичной информации, измеряющие углы или угловые скорости поворота ЛА и линейные ускорения (акселерометры и физические маятники). Эти датчики устанавливаются непосредственно на борту ЛА и работают совместно с цифровой или аналоговой вычислительной машиной, непрерывно производя расчет углов курса, крена и тангажа или иных параметров, определяющих ориентацию ЛА относительно базовой системы координат [1, 3, 9, 12].

В бесплатформенных системах ориентации и навигации гироскопы и акселерометры устанавливаются непосредственно на корпусе ЛА либо монтируются в специальные блоки чувствительных элементов. Сигналы этих датчиков поступают на вход ЭВМ, которая решает задачу ориентации аналитически, как бы, заменяя собой карданов подвес и координатный преобразователь гироплатформы.

Наибольшее распространение в бесплатформенных системах ориентации и навигации получают прецизионные датчики угловых скоростей (ДУС) и гироскопы на электростатическом подвесе, определяющие углы поворота ЛА вокруг центра его масс; также используются угловые и линейные акселерометры, установленные определенным образом на корпусе ЛА [1, 9, 21]. В отличие от систем ориентации с гироплатформами в бесплатформенных системах гироскопические датчики и акселерометры работают в более тяжелых условиях эксплуатации вследствие изменения расположения приборов по отношению к направлению гравитационного поля Земли, больших скоростей и ускорений, возникающих при вращении, колебаниях и вибрации корпуса ЛА [1].

Точность же измерения угловых скоростей, ускорений или угловых перемещений КА должна быть того же уровня, который достигнут в системах платформенного типа.

Датчики угловых скоростей – это один из основных и наиболее совершенных чувствительных элементов систем управления, стабилизации и навигации [21].

К характеристикам ДУС предъявляются очень жесткие требования. Так, верхний диапазон скоростей, измеряемых современными ДУС, соответствует десяткам и сотням градусам в секунду. Верхний диапазон входных воздействий, в котором ДУС обязан обеспечивать измерения угловой скорости, достигает 100 Гц [21].

Прецизионные ДУС бесплатформенных инерциальных систем должны иметь разрешающую способность до тысячных долей градусов в час и линейность до 10^-3%, причем эти ДУС должны формировать выходной сигнал в цифровом виде. В широком диапазоне варьируются требования к массовым и габаритным параметрам приборов; из-за миниатюризации ДУС в последнее время значительно уменьшились величины собственного кинетического момента их гироскопов [1, 9, 12, 21].

Датчик угловой скорости (ДУС) служит для измерения угловой скорости КА от 0,001 до 10 с^-1 в инерциальном пространстве. Для этой цели можно применять как двухстепенные, так и трехстепенные гироскопы. Гиротахометр (рис. 2.2) представляет собой обычно гироскоп с двумя степенями свободы и жесткой отрицательной обратной связью, которая создает противодействующий момент, пропорциональный угловому отклонению рамки от исходного положения для получения приемлемых переходных процессов применяются специальные демпферы; если гироскоп помещается в поплавок, то демпфирование осуществляется жидкостью [1, 21].

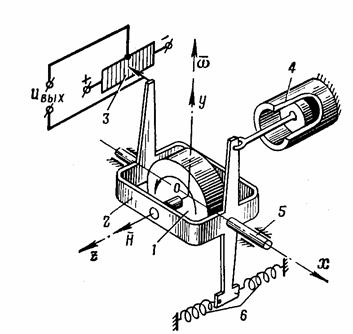
Рис. 2.2 - Кинематическая схема гиротахометра:

1 – ротор; 2 – рамка; 3 – датчик сигнала; 4 – демпфер; 5 – цапфа выходной оси; 6 – пружины; Н – кинетический момент гироскопа.

Величина момента сухого трения М₀, определяет порог чувствительности гироскопа по отношению к измеряемой скорости. В поплавковых гироскопах момент М₀ пренебрежимо мал. Поэтому в установившемся режиме угол поворота рамки относительно ее оси [21]

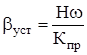
К_пр – приведенная жесткость пружины.

ГИВУС включает в себя шесть измерителей с некомпланарным расположением осей чувствительности (измерительных осей).

Все шесть измерительных осей ( 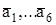) при номинальном положении располагаются параллельно ребрам базового правильного шестигранника, вписанного в конус вращения с углом полураствора j, равным 0,9553 рад, и имеющего симметричное расположение ребер по кругу основания конуса с угловым шагом q, равным 1,04 рад [21].

1. В качестве приборной системы координат принимается правая ортогональная Ox_пy_пz_п, материализованная посадочными местами на корпусе ГИВУС. Ориентация осей чувствительности ГИВУС относительно осей приборной системы координат приведена на рисунке (рис 2.3) где:

Ox_пy_пz_п – приборная система координат ГИВУС;

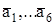 – положительные направления осей чувствительности ГИВУС (измерителей А₁, А₂, А₃, А₄, А₅, А₆ соответственно).

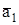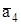Оси чувствительности  и  параллельны плоскости х_пОу_п. На рисунке (рис. 2.4) показаны положительные направления углов отклонения осей чувствительности измерителей относительно номинального положения, где

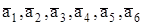 – номинальные положения осей чувствительности измерителей А₁, А₂, А₃, А₄, А₅, А₆ соответственно;

Dq₁, Dj₁, Dq₂, Dj₂,…, Dq₆, Dj₆ – положительные углы отклонения осей относительно номинального положения.

2. При вращении ГИВУС вокруг оси чувствительности 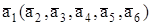 в положительном направлении (против часовой стрелки, если смотреть с конца вектора) выходная информация с измерителя А₁ (А₂, А₃, А₄, А₅, А₆) соответствует положительному значению параметра и наоборот.

3. Относительная ориентация осей приборной системы координат и строительной системы координат изделия такова, что ось х_п совпадает с отрицательным направлением оси z_изд; ось у_п с положительным направлением оси х_изд; z_п совпадает с отрицательным направлением оси у_изд.

C гивус выходная информация в дискретном виде выдается с каждого измерителя (А₁, А₂, А₃, А₄, А₅, А₆) в виде унитарного кода – последовательности импульсов, транслируемых в БЦВК по электрически не связанным каналам. Каждый канал информации имеет две функциональные линии связи; по одной линии выдаются импульсы, соответствующие положительной проекции, а по другой линии, соответствующие отрицательной проекции угловой скорости на ось чувствительности измерителя [1, 3, 9, 21].

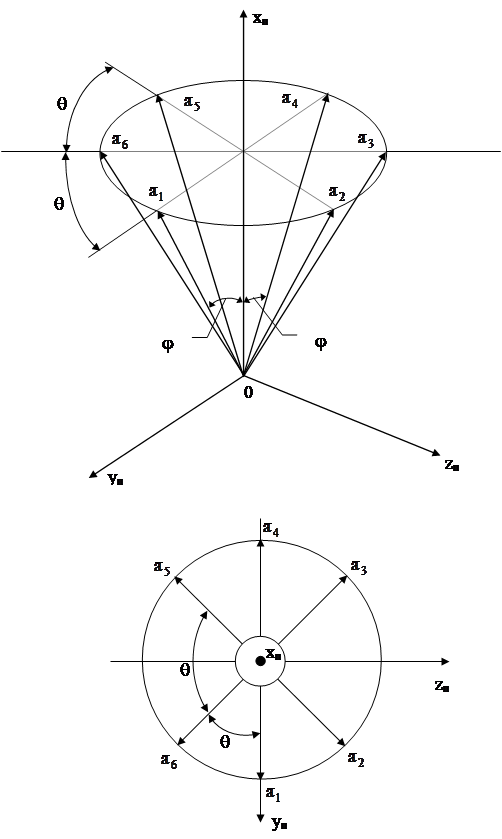
Рис. 2.3 - Ориентация осей чувствительности ГИВУС относительно осей приборной системы координат

Рис.2.4 - Положительные направления углов отклонения осей чувствительности измерителей относительно номинального положения

МАТЕМАТИЧЕСКИЕ МОДЕЛИ