7.1 Типовые функциональные звенья и общие положения по применимости и элементной базе.
Из элементов УСЭППА (Универсальная система элементов промышленной пневмоавтоматики) при разработке регулирующих устройств пневмоавтоматики формируются различные сочетания – соединения, которые реализуют определенные функциональные зависимости выходного сигнала от входного. Так как эти соединения используются во многих устройствах, выпускаемых отечественной приборостроительной промышленностью, и в динамическом отношении являются типовыми элементарными звеньями, то их целесообразно рассмотреть отдельно.
Апериодическое звено. Принципиальная пневматическая и структурная схемы соединения из элементов УСЭППА, реализующие апериодическое звено, представлены на рис. 7.1.. Звено образуется с помощью переменного пневмосопротивления с проводимостью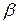 
и пневмоемкостью 
.
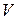Расход воздуха через пневмосопротивление пропорционален перепаду давления на нем:
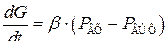, (7.1)
где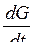 
– массовый расход воздуха через пневмосопротивление в единицу времени; 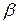– проводимость пневмосопротивления; 
и 
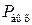– давление на входе и выходе соединения соответственно.
Уравнение универсального газового закона для пневмоемкости имеет вид
, (7.2)
где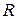 
– универсальная газовая постоянная, равная 2930 см/К;
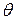– абсолютная температура.
С учетом (7.1) выражение (7.2) запишется в виде
,
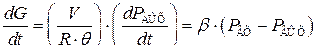или
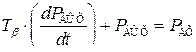, (7.3)
где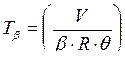 
– постоянная времени апериодического звена.
Передаточная функция апериодического звена находится из выражения:
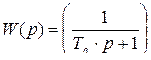. (7.4)
Параметром настройки апериодического звена является его постоянная времени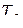 
. Она определяется по экспериментальной переходной характеристике звена, полученной при ступенчатом единичном входном воздействии.
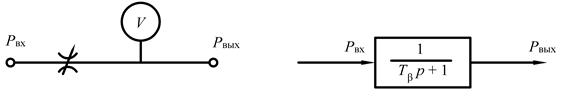
а) б)
Рис. 7.1. Апериодическое звено
а) принципиальная пневматическая схема;
б) структурная схема
Апериодическое звено демпфирует входной сигнал. В связи с этим в структурных схемах автоматических регуляторов постоянная времени апериодического звена часто обозначается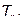 
. Чем больше постоянная времени 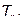, тем больше инерционность апериодического звена и тем больше демпфируется входной сигнал.
Интегрирующее звено. Если к выходу мембранного сумматора подключить апериодическое звено, охваченное положительной обратной связью, то из элементов УСЭППА можно составить устройство с интегрирующими свойствами (Рис. 7.2.). Условие равновесия мембранного сумматора, приведенного на рис. 7.2., а
.
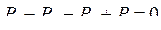Поскольку для апериодического звена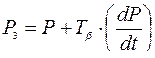 
, то
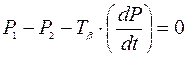, (7.5)
откуда
.
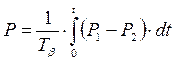Следовательно, схема на рис. 7.2., а выполняет операцию интегрирования разности входных делений 
.
Дифференциальное уравнение (7.5) после преобразования по Лапласу примет вид
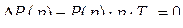, или 
.
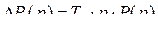Передаточная функция интегрирующего звена определяется из выражения
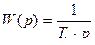, (7.6)
где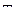 
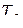= – постоянная времени интегрирования.
Передаточную функцию интегратора можно найти по его структурной схеме, изображенной на рис. 7.3., б. Апериодическое звено с передаточной функцией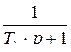 
охвачено положительной обратной связью. Передаточная функция такого соединения
.
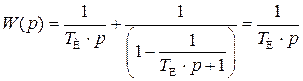а) б)
Рис. 7.3. Интегратор
а) принципиальная пневматическая схема;
б) структурная схема
Параметром настройки интегрирующего звена является его постоянная времени 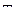, определяемая из переходной характеристики интегратора.
Звено прямого предварения. Операция дифференцирования (прямого предварения) на элементах УСЭППА может быть реализована как на пяти-, так и на трехмембранных сумматорах. Рассмотрим наиболее часто применяющиеся схемы дифференцирования – звенья прямого предварения, реализованные на трехмембранных сумматорах и представленные на рис. 7.4. При реализации звеньев прямого предварения сопло С2 трехмембранного сумматора заглушается и в работе не участвует.
Условие равновесия сумматора, включенного по схеме рис. 7.4. а, имеет вид
, (7.7)
где 
– выходное давление апериодического звена, образованное переменным дросселем с проводимостью 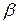и пневмоемкостью 
, 
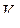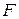и 
– площади большой и малой мембран сумматора;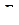 
– входное давление; 
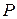– выходное давление звена прямого предварения.
Переходные процессы в апериодическом звене определяются дифференциальным уравнением
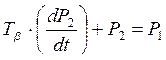. (7.8)
Уравнения (7.7) и (7.8) после преобразований по Лапласу будут иметь вид
;
.
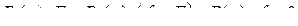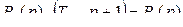Решив совместно эти уравнения, после исключения из них промежуточной переменной 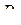(p) получим
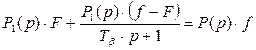(7.9)
или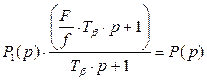 
.
Передаточная функция звена прямого предварения
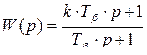, (7.10)
где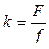 
– коэффициент передачи звена. Для трехмембранного сумматора 
.
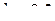Представим передаточную функцию (7.10) звена в виде
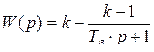. (7.11)
Из (7.11) следует, что дифференциатор – звено прямого предварения, выполненное по схеме на рис. 7.4. а, структурно можно представить как параллельное соединение усилительного звена с передаточной функцией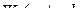 
и апериодического звена с передаточной функцией 
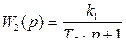, выходной сигнал которого суммируется с выходным сигналом звена 
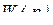с обратным знаком (Рис. 7.4. б).
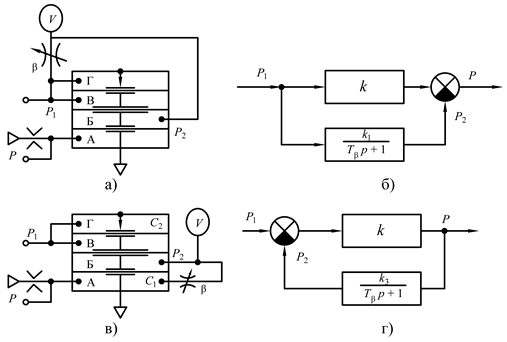
Рис. 7.4. Схемы звеньев прямого предварения.
а) и в) принципиальные пневматические схемы;
б) и г) структурные схемы.
При этом,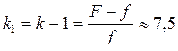 
. (7.12)
Из (7.10) видно, что звено, выполняемое по схеме на рис. 7.4. а, в динамическом отношении является интегродифференцирующим.
Так как отношение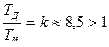 
, то в целом это интегродифференцирующее звено обладает дифференцирующими свойствами.
На рис. 7.4., в усилитель включен по схеме повторения и охвачен инерционной отрицательной обратной связью, подаваемой с выхода инерционного звена в камеру Б. В схеме на рис. 7.4. в, давление, формирующееся на выходе звена, определяется выражением
. (7.13)
Решая совместно (7.8) и (7.13), получаем
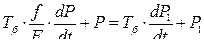. (7.14)
С учетом этого передаточная функция звена, выполненного по схеме на рис. 7.4., в, определяется выражением
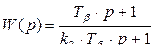, (7.15)
где,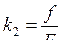 
– коэффициент передачи, 
.
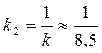Так как для схемы на рис. 7.4., в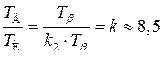 
, то в динамическом отношении схемы включения на рис. 7.4., а и 7.4., в эквивалентны.
Структурная схема дифференцирования, выполненная по схеме на рис. 7.4., в представлена на рис. 7.4., г. Коэффициент передачи апериодического звена обратной связи
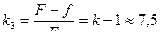. (7.16)
Дифференциальный делитель давления. В различных устройствах пневмоавтоматики находят широкое применение дифференциальные делители давления из переменных и постоянных пневмосопротивлений (дросселей), образующих четырехполюсник на два входа и два выхода, принципиальная схема которого представлена на рис. 7.5. Дифференциальный делитель давления по каналам 1-3 и 2-3 можно представить как дроссельный сумматор, для которого по каналу 2-3 роводимости α2 и β дросселей II и III
Соединены последовательно.
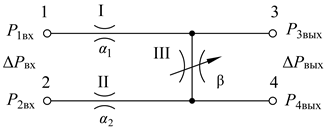
Рис. 7.5. Принципиальная пневматическая схема дифференциального
делителя давления.
С учетом этого запишем
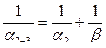, откуда 
,
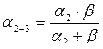где α2-3 - проводимость дифференциального делителя давления по каналу 2-3.
Исходя из принципа работы дроссельного сумматора можно записать
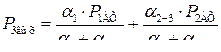, или
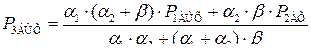. (7.18)
Аналогично,
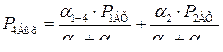, или
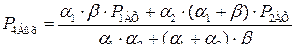, (7.19)
где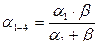 
- проводимость дифференциального делителя давления по каналу 1-4.
Если за вход дифференциального делителя давления принять разность 
, а за выход разность , то с учетом (7.18) и (7.19) получим
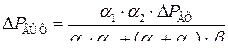(7.20)
или,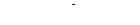 
, (7.22),
где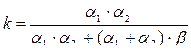 
(7.23)
- коэффициент передачи дифференциального делителя давления по каналу « 
».
В пневматических регулирующих устройствах проводимости постоянных дросселей α1 и a2, как правило, примерно равны.
В этом случае коэффициент передачи (7.23) будет равен
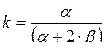. (7.24)
При полностью закрытом переменном дросселе b®0,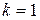 
; при полностью открытом b®¥, k =0.
Таким образом, при настройке дифференциального делителя давления, регулируя степень открытия переменного дросселя, коэффициент передачи можно плавно изменять от 0 до 1.
Дата: 2019-04-23, просмотров: 450.
