В связи с тем, что БИНС устанавливается на ЛА и измеряет его навигационные параметры, нам необходимо построить модель движения ЛА. Выбранный летательный аппарат имеет следующие параметры:
Таблица 11
| № | Обозначение | Значение | Размерность | Комментарий |
| 1 | Qt | 1.527778 | - | коэффициент расхода топлива |
| 2 | S | 260 | кв м | площадь крыльев |
| 3 | m | 115000 | кг | масса ЛА |
| 4 | Rf | 2.130 | м | плечо вектора тяги |
| 5 | Ix | 5000000 | кг*кв м | осевой момент инерции |
| 6 | Iy | 16000000 | кг*кв м | осевой момент инерции |
| 7 | Iz | 11000000 | кг*кв м | осевой момент инерции |
| 8 | Ixy | -400000 | кг*кв м | центробежный момент инерции |
| 9 | SAH (LMU) | 6.608 | м | средняя аэродинамическая хорда |
| 10 | l (HS) | 22.42 | м | размах крыльев |
| 11 | XSP | 30 | % | центровка относительно САХ |
| 12 | LAM | 7.730 | - | коэффициент влияния подъемной силы на лобовое сопротивление |
| 13 | F0 | 182353.2 | Н | максимальная тяга |
Движение ЛА
При исследовании движения в различных режимах полета ЛА рассматривается как твердое тело, симметричное относительно основной плоскости связанной СК (вертикальной плоскости), на которое действуют аэродинамические силы и сила тяги, вектор которой находится в плоскости симметрии ЛА и проходит через центр масс ЛА. Таким образом, уравнения движения в векторной форме имеют вид:
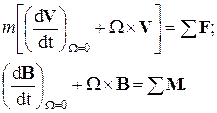(4)
где:
F- вектор сил, действующих на ЛА;
M- вектор моментов, действующих на ЛА;
B- вектор количества движения;
V- вектор линейной скорости;
W- вектор угловых скоростей;
m- масса ЛА.
При исследовании движения указанные векторы раскладываются на проекции по осям соответствующей системы координат (скоростной, связанной, экспериментальной и земной).
Поскольку имеют место дифференциальные уравнения, их необходимо привести к форме Коши, наиболее удобной для интегрирования:
, 
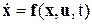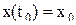
где:
x – вектор состояния;
u – вектор действующих факторов;
t – время.
Для формирования системы уравнений (4) в форме Коши, описывающей пространственное движение самолета используют уравнения динамики и кинематики движения центра масс самолета и уравнения динамики и кинематики движения самолета относительно центра масс.
Уравнения движения центра масс самолета в проекциях на оси скоростной системы координат имеют вид:
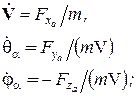(5)
где:
, 
, 
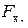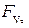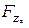- проекции результирующего вектора внешних сил (аэродинамической силы A, силы тяжести G) и тяги двигателей P на оси скоростной системы координат;
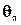- скоростной угол наклона траектории;
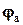- скоростной угол пути;
V- скорость самолета.
Кинематические уравнения движения центра масс ЛА в проекциях на оси земной СК могут быть записаны в виде:
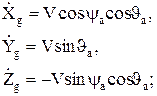(6)
где:
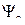- скоростной угол курса;
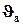- скоростной угол тангажа;
Xg, Yg, Zg- координаты самолета в земной системе координат.
Эти же уравнения, выраженные через основные углы имеют вид (7) :
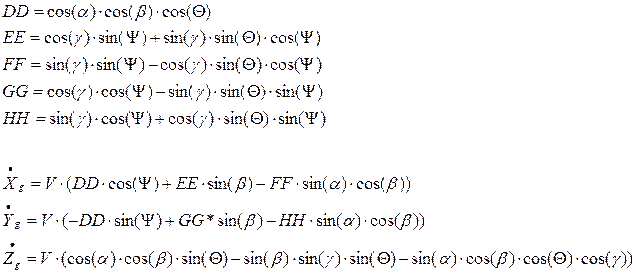
где:
DD, EE, FF, GG, HH – вспомогательные выражения для облегчения читаемости формул;
α – угол атаки;
β – угол скольжения;
γ – угол крена;
Ψ – угол курса;
Θ – угол тангажа.
Динамические уравнения движения самолета относительно центра масс записываются в форме:
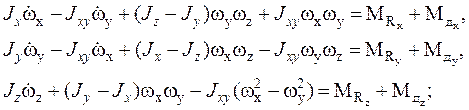(8)
где:
Jx, Jy, Jz- осевые моменты инерции самолета, заданные выше при описании параметров самолета;
Jxy- центробежный момент инерции самолета, заданный при описании параметров самолета;
, 
, 
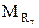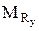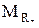- проекции результирующего момента аэродинамических сил M на оси связанной системы координат;
, 
, 
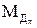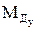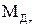- проекции момента дебаланса тяги двигателей MД на оси связанной системы координат;
, 
, 
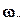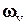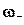- проекции вектора угловой скорости на оси связанной системы координат.
Для записи системы 8 в форме Коши необходимо из нее выделить производные проекций угловых скоростей:
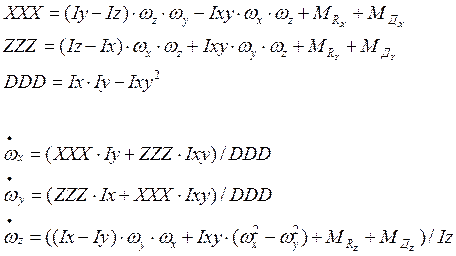(9)
Кинематические уравнения движения самолета относительно центра масс имеют вид:
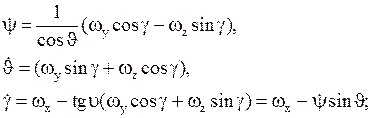(10)
где:
ψ- угол курса;
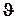- угол тангажа;
g- угол крена.
Изменение массы самолета происходит по следующему закону:
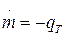(11)
где
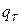- расход топлива,
.
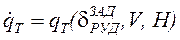Итак, для построения модели движения нашего самолета нам понадобятся системы дифференциальных уравнений 5, 7, 9, 10 и 11. Схема с уравнениями движения ЛА представлена на рисунке 17.
Аэродинамика
Аэродинамические силы и моменты могут задаваться в скоростной, связанной и экспериментальной системах координат. Мы будем использовать выражения в экспериментальной системе координат:
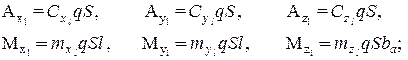(12)
где:
, 
, 
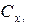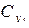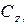-коэффициенты аэродинамических сил в экспериментальной системе координат;
, 
, 
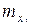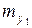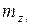- коэффициенты аэродинамических моментов в экспериментальной системе координат;
q – скоростной напор,
,
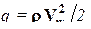r - плотность воздуха;
Vw- воздушная скорость;
S – площадь крыла самолета;
l – размах крыла самолета;
ba- средняя аэродинамическая хорда крыла самолета;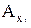 
, 
, 
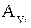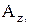- проекции аэродинамической силы на оси экспериментальной системы координат;
, 
, 
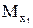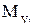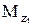- проекции аэродинамического момента на оси экспериментальной системы координат.
Коэффициенты аэродинамических сил и моментов зависят от многих параметров и определяются довольно громоздкими формулами. Подробнее о реализации аэродинамики самолета см. в приложении к пояснительной записке (в исходном коде программы и списке идентификаторов программы).
Модель ветра
В описании аэродинамики упоминалась воздушная скорость самолета. Она прямым образом зависит от наличия воздействия внешней среды (ветра). Это видно из формул:
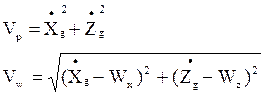
где:
Vp – путевая скорость самолета;
Vw – воздушная скорость самолета;
Wx, Wz – составляющие скорости ветра.
Как видно, при отсутствии ветра воздушная скорость влияния не имеет, так как вырождается в путевую.
Для учета воздействия внешней среды нам необходимо построить модель ветра и определить упомянутые выше скорости ветра и его ускорения. Определим их как порывы ветра турбулентной атмосферы с дисперсиями по составляющим равными 1 метр в секунду:
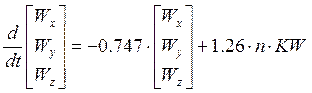(13)
где:
n – случайное число из набора случайных чисел [-1;1] с нормальным законом распределения;
KW = 8.6 – коэффициент, значение которого подобрано так, что дисперсии скорости ветра по составляющим = 1 метр в секунду.
Траектория полета
Поскольку мы разрабатываем модель движения ЛА, то необходимо задаться и вопросом – а куда и как собственно самолет летит!? Для решения этого вопроса необходимо построить и задать траекторию полета, движение ЛА на которой мы и будем моделировать.
Для простоты отладки модели зададим несложную траекторию, состоящую из трех участков:
Рисунок 18. Заданная траектория полета
Считаем, что первый участок полета – горизонтальный полет на Восток. Соответственно, третий участок – это полет на Север.
Для полноты задания траектории полета в модели движения ЛА необходимо задать такие параметры для каждого участка полета, как угол скольжения, крена, курса, угловые скорости по всем трем осям, угол наклона траектории.
Первый участок полета – горизонтальный полет. Так как с него начинается полет ЛА, то первым делом зададим скорость полета V0 = 230 м/с и высоту полета H0 = 11000 м, а также начальную массу ЛА M0 = 115000 кг. Так как полет горизонтальный то значит все проекции угловой скорости на оси связанной СК равны 0 рад./с. (ωx0 = 0, ωy0 = 0, ωz0 = 0). Углы скольжения и крена тоже зададим равными 0 рад. (β0 = 0, γ0 = 0). Угол наклона траектории GAM равен 0 рад. Поскольку на первом участке мы летим на Восток, то угол курса будет равен 90 град. (ψ0 = 90).
Второй участок полета – поворот на 90 град в течении 273 с. Значит угол крена имеет отличное от 0 значение. Зададим его равным 0.2 рад/с. Проекции угловой скорости на оси связанной СК ωy0 и ωz0 имеют такие значения, чтобы обеспечить поворот на 90 град. С заданным креном в заданное время. Эти значения рассчитываются следующим образом:
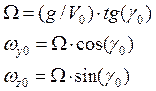
где: Ω – угловая скорость поворота.
Угол скольжения при повороте немного увеличивается и равен 0.02 рад. Угол наклона траектории GAM по прежнему равен 0 рад.
Третий участок полета – горизонтальный полет, как и первый участок. Соответственно, все параметры равны заданным на первом участке за исключением скорости, высоты (они задаются один раз в самом начале полета) и курса – так как теперь полет происходит на Север, то угол курса = 0 град.
Количество участков полета и их направление задается в полетном задании. Оно выглядит следующим образом и находится в папке \\PZ:
Полетное задание:
-----------------------------------
КORT=3 количество ортодромий
SX1 = 10000.0 длина ортодромии
PSIG1 = 0.0 рыскание ортодромии
SX2 = 10000.0 длина ортодромии
PSIG2 = 90.0 рыскание ортодромии
SX3 = 10000.0 длина ортодромии
PSIG3 = 0.0 рыскание ортодромии
По окончании программа выдает окно с результатами по времени, сколько было потрачено на каждый участок:
Балансировка
Балансировочные значения параметров самолета позволяют обеспечить выдерживание заданного режима полета при отсутствии возмущающих воздействий со стороны внешней среды. Эти значения определяют установившийся режим полета, когда силы и моменты, действующие на самолет, уравновешивают друг друга и обеспечивается его равномерное движение.
Отсюда следует, что балансировочные значения параметров самолета могут быть определены исходя из уравнений динамики, если приравнять в них нулю выражения, определяющие действующие на самолет ускорения.
При горизонтальном полете система трех нелинейных алгебраических уравнений содержит три неизвестных параметра, которыми являются тяга двигателей, угол атаки и отклонение руля высоты. Решением являются балансировочные значения этих параметров, которые обеспечивают установившееся движение самолета. Кроме того, в режиме поворота есть два дополнительных искомых параметра: отклонение руля элеронов и отклонение руля направления при заданной угловой скорости поворота.
Решение задачи поиска балансировочных параметров сводится к минимизации по искомым параметрам функции, образованной суммами квадратов правых частей решаемых нелинейных уравнений, которое осуществляется методом вращающихся координат.
Таким образом, при разработке модели движения ЛА по заданной траектории необходимо проводить балансировку самолета перед началом полета на каждом из участков траектории. В нашем случае нам необходимо три раза провести такие действия, так как мы задались траекторией, состоящей из трех участков.
Подробнее о поиске балансировочных параметров см. в приложении к данной пояснительной записке (в исходном коде программы).
Модель управления ЛА
Для полноты разрабатываемой модели полета ЛА нам необходимо реализовать модель его управления. Строго говоря, синтез законов управления – это довольно сложная вещь, которой отведена целая отрасль науки. Мы же ограничимся режимом стабилизации в качестве управления нашим самолетом. Назначением данного режима является автоматическая стабилизация углового положения летательного аппарата относительно заданного невозмущенного положения (балансировочного). По самому своему назначению это – режим малых отклонений, при котором обычно можно использовать линейные модели (линейные уравнения) объекта управления.
В рамках рассматриваемого режима стабилизации продольное и боковое движения являются независимыми, автономными. Ясно, что критерии оптимальности – функционалы для этих движений должны быть независимыми, т. е. содержащими автономные группы фазовых координат и управлений. Оптимальные управления при этом получаются также независимыми и могут синтезироваться путем решения двух автономных задач.
В рассматриваемой полной линейной модели продольного движения отклонения скорости полета и угловые отклонения взаимосвязаны. Поэтому синтез собственно автопилота-стабилизатора углового положения в строгой постановке должен осуществляться одновременно с синтезом стабилизатора скорости (автомата тяги).
Стабилизация для контуров продольного движения:
Для контуров стабилизации продольного движения немаловажную роль играет инерционность исполнительных устройств. Для краткости ограничимся простейшими линейными моделями исполнительных устройств в виде апериодических звеньев:
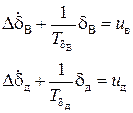
Для рассматриваемого самолета принят следующие закон управления на указанном маршруте:
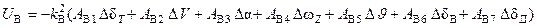
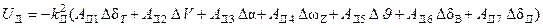
где:
Ui – синтезируемые управления (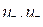 
);
Ki , Aij –постоянные положительные коэффициенты;
Δ – отклонение параметров состояния.
Датчики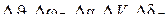 
будем считать безинерционными.
Рассмотрим теперь задачу синтеза контуров стабилизации крена, рысканья и скольжения, т. е. задачу синтеза системы стабилизации бокового движения.
Стабилизация для контуров бокового движения:
Уравнении исполнительных устройств канала элеронов и канала руля направления:
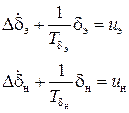
Для рассматриваемого самолета принят следующие закон управления на указанном маршруте:
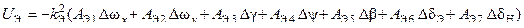
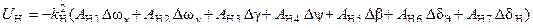
где:
Ui – синтезируемые управления;
Ki , Aij –постоянные положительные коэффициенты;
Δ – отклонение параметров состояния.
Подробно написанные режимы стабилизации для всех контуров см. в приложении к данной пояснительной записке (в исходном коде программы).
Итак, рассмотрев все аспекты и проблемы создания модели полета ЛА по заданному маршруту, можно сделать следующий вывод: для реализации такой общей модели необходимо в совокупности решить уравнения 5, 7, 9, 10, 11, учитывая аэродинамику ЛА (12), воздействие внешней среды (13), балансировку ЛА на каждом участке маршрута и принятые законы стабилизации.
Алгоритм моделирования
В рамках данной работы необходимо разработать программное обеспечение (программный продукт), который будет в комплексе реализовывать все рассмотренные выше математические модели.
Такой программный продукт (ПП) был разработан средствами оговоренного выше языка программирования. Он получил название СКМ.DSP. Компакт-диск с программой (СКМ.DSP), ее описанием, полным проектом в Visual C++ и всей документацией приложен к данной пояснительной записке.
В программе учтены все рассмотренные модели, а интегрирование проводилось численным методом Рунге-Кутта 4 порядка с постоянным шагом интегрирования. Поскольку на сегодняшний день программирование приняло объектно-ориентированный вид, то при разработке ПП тоже использовался такой подход, и все рассмотренные модели сделаны в виде отдельных функций; также написана основная функция моделирования, которая управляет взаимодействием всех остальных функций.
Перечень всех основных функций и их описаний приведен в таблице 12 (в связи с громоздким синтаксисом функций в таблице представлены упрощенные варианты, дающие общее представление о функции). Для подробного ознакомления с синтаксисом программы см. приложение к данной пояснительной записке (исходный код программы):
Таблица 12
| № | Функция | Описание |
| 1 | AISB ( ) | Функция реализует алгоритм инициализации состояния борта |
| 2 | AIVSO ( ) | Функция реализует алгоритм инициализации вектора состояния объекта |
| 3 | AZPZ ( ) | Функция реализует алгоритм загрузки полетного задания |
| 4 | DISPBAL ( ) | Функция реализует диспетчер процедур расчета балансировочных параметров |
| 5 | HORIZBAL ( ) | Функция, реализующая процедуры расчета балансировочных параметров при горизонтальном полете |
| 6 | TURNBAL( ) | Функция, реализующая алгоритм расчета балансировочных параметров при повороте |
| 7 | DISPCKM ( ) | Функция, реализующая диспетчер моделирующего комплекса |
| 8 | RK4 ( ) | Функция реализующая алгоритм интегрирования методом Рунге-Кутта 4 порядка |
| 9 | AEROFLU ( ) | Функция, реализующая аэродинамику объекта (расчет коэффициентов аэродинамических сил и моментов) |
| 10 | OBEKT ( ) | Функция, реализующая модель пространственного движения объекта |
| 11 | AFUVRO ( ) | Функция, реализующая модель автопилота (законы стабилизации), алгоритмы формирования управляющих воздействий на рулевые органы |
| 12 | AONP ( ) | Функция, реализующая алгоритм определения навигационных параметров |
| 13 | ARVP ( ) | Функция, реализующая алгоритм расчета требуемых (выдерживаемых законом управления) параметров |
| 14 | SREDA( ) | Функция, реализующая модель воздействия ветра |
| 15 | TLM ( ) | Функция, реализующая алгоритмы записи параметров состояния в файлы телеметрии |
| 16 | AIUUS ( ) | Функция, реализующая алгоритм измерения ускорения и угловой скорости |
| 17 | COMMON ( ) | Функция, содержащая функции общего назначения |
| 18 | PAR( ) | Функция, содержащая все глобальные идентификаторы |
| 19 | PKS (), WRK50() | Функции, реализующие в совокупности минимизацию заданной функции методом вращающихся координат и поиск балансировочных параметров при горизонтальном полете |
| 20 | FCT | Функция, возвращающая сумму квадратов правых частей уравнений для балансировки |
| 21 | FORMDYT (), DEFORMDYT () | Функции, реализующие алгоритмы формирования/деформирования вектора интегрируемых параметров |
| 22 | AMIN () | Функция, реализующая алгоритм сравнения 2х чисел и выбора наименьшего |
| 23 | AMAX () | Функция, реализующая алгоритм сравнения 2х чисел и выбора наибольшего |
| 24 | Matrixmult ( ) | Функция реализует произведение двух матриц размерностями до 3х3 |
| 25 | MatrixSum () | Функция реализует процедуру сложения 2х матриц 3х3 |
| 26 | CHANCE () | Функция реализует процедуру формирования случайных чисел с нормальным законом распределения и СКО = 1.0 |
| 27 | Generator () | Функция реализует процедуру - генератор случайных нормальных распределений чисел в интервале [-1;1] |
Рассмотрев все основные функции, теперь мы можем наглядно представить алгоритм работы программы. Он представлен в виде блок-схемы на рисунке 6. Отметим, что в представленном алгоритме опущены второстепенные функции типа AMIN,… в связи с тем, что схема получится слишком нагроможденной.
 |  |
 | |||
 | |||
Дата: 2019-04-23, просмотров: 269.
