Задачи автоматического управления на всех этапах полета. Законы управления КСУ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

I. ВВЕДЕНИЕ

Темой данной дипломной работы является моделирование точности работы бесплатформенной инерциальной навигационной системы (БИНС) в контуре беспилотного летательного аппарата.

БИНС предназначена для определения и индикации основных параметров полета ЛА, таких как: навигационные параметры и параметры ориентации, ускорения (угловые и линейные), скорости на текущий момент полета и т. Д.

В состав БИНС входят интегральный блок датчиков, состоящий из трех акселерометров, трех гироскопов и четырех датчиков внутренней температуры блока, и цифровой вычислитель. БИНС выполняет функцию основного автономного измерителя автопилота. Автопилот реализуется на основе принципа стабилизации балансировочных параметров для данного режима полета. Балансировочные параметры летательного аппарата позволяют обеспечить выдерживание заданного режима полета при отсутствии возмущающих воздействий со стороны внешней среды.

В данной дипломной работе помимо изучения работы системы БИНС, также определяются ее достоинства и недостатки. Основная задача работы это моделирование полета летательного аппарата с системой БИНС на борту. На основе моделирования определяется влияние компенсации температурных погрешностей чувствительного элемента БИНС на точность движения летательного аппарата. Конечный программный продукт реализован на языке программирования С++ с использованием сред Microsoft Visual Studio 6.0.

В экономической части производится обоснование экономической целесообразности моделирования бесплатформенной инерциальной навигационной системы при использовании более современных комплектующих, определяются показатели экономического обоснования и экономическая эффективность разработки. Также определяются трудоемкость и затраты.

В разделе «Охрана труда и окружающей среды» производится анализ условий труда и расчет необходимого искусственного освещения.

II. РАСЧЕТНАЯ ЧАСТЬ

Интегральный блок датчиков (ИБД)

На базе твердотельных датчиков угловых скоростей (ДУС) и датчиков линейных ускорений (ДЛУ) целесообразно объединение датчиков в единый измерительный блок, где сигналы обрабатываются цифровым вычислителем и в последовательном коде выдаются в основной вычислитель системы управления. Так сделано, например, в интегральном блоке датчиков.

В вычислитель блока датчиков можно включить функцию приема и обработки аналоговых сигналов, их преобразование в цифровой код и передачу в цифровом виде потребителям.

ИБД обеспечивает измерение угловых скоростей и линейного ускорения в связанных осях самолета, преобразование этих и других сигналов датчиков, входящих в систему, и выдачу выходных сигналов в виде последовательного цифрового кода.

Интегральный блок датчиков разработан на основе волоконно-оптических датчиков угловой скорости типа ДУСв-5 и твердотельных акселерометров типа АТ1112 и предназначен для применения в системах дистанционного или автоматического управления. Упрощенная структурная схема системы автоматического управления представлена на рисунке 2:

Рисунок 2. Упрощенная структурная схема САУ.

ИБД принимает аналоговые сигналы с датчиков первичной информации, которые затем обрабатываются вычислителем, входящим в состав ИБД, и выдает сигналы в цифровом последовательном коде на центральный вычислитель системы. После обработки и перевода сигнала в аналоговый, информация с центрального вычислителя поступает на усилитель, который в свою очередь преобразует сигнал и предает его на управляющие органы.

Функциональная схема представлена на рисунке 3:

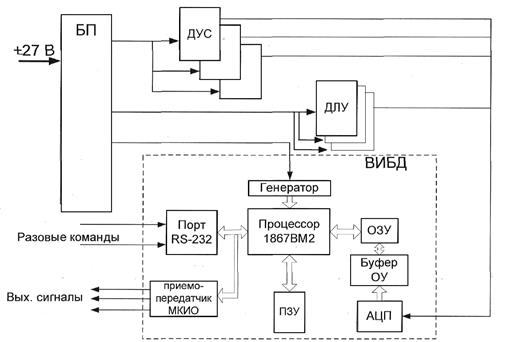
Рисунок 3. Функциональная схема ИБД.

Использование волоконно-оптического датчика в составе ДУСа в ИБД определяет уникальные свойства прибора:

- потенциально высокая чувствительность (0.01 град/сек и менее);

- малые габариты и масса конструкции, благодаря возможности создания ВОГ на интегрально-оптических схемах;

- невысокая стоимость производства и относительная простота технологии по сравнению с роторными гироскопами;

- низкое потребление энергии;

- большой динамический диапазон измеряемых угловых скоростей;

- отсутствие вращающихся механических элементов (роторов) и подшипников, что повышает надежность;

- практически мгновенная готовность работы (не затрачивается время на раскрутку ротора);

- низкая чувствительность к линейным ускорениям;

- высокая помехоустойчивость;

Одним из наиболее важным свойством ИБД является его высокая надежность (безотказность). Аналогичное устройство блок гироскопичекских датчиков имеет гарантийную наработку 6000 ч, в то время как у ИБД средняя наработка на отказ и повреждение составляет 10000 ч.

В состав ИБД входят:

- три волоконно-оптических датчика ДУСв-5;

- три твердотельных акселерометра АТ1112;

- цифровой вычислитель;

- блок питания;

- четыре датчика внутренней температуры.

Расположение датчиков в блоке ИБД представлено на рисунке 4:

n_X

ω_Y

ωz

ω_X

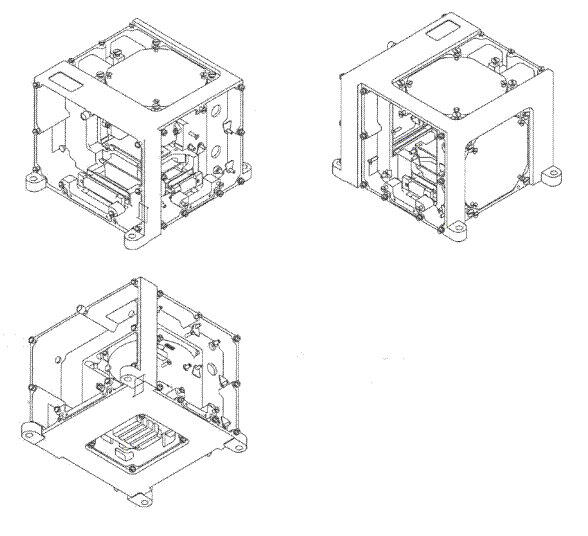
Рисунок 4. Расположение датчиков внутри ИБД.

Внешний вид и габаритные размеры представлены на рисунке 5:

Рисунок 5. Внешний вид ИБД.

Крепление датчиков осуществляется 4 винтами М-4 к крышке корпуса по соответствующим координатным осям X, У, Z. Блок питания БПП и вычислитель ВИБД крепятся к корпусу 9 винтами М-4.

Точность установки датчиков (привязки осей к корпусу) должна составлять не более ±15'.

На корпус ИБД необходимо нанести гравировку с указанием названия изделия, его номер, а так же направление координатных осей.

Корпус необходимо выполнить с анодирующим покрытием, которое защищает от коррозии.

Вес интегрального блока датчиков не должен превышать 2,6 кг.

ИБД должен быть стойким к внешним воздействиям, представленным в таблице 1:

Таблица 1

Внешние воздействующие факторы	Характеристики воздействующих факторов	Максимальные значения величины воздействующего фактора, степени жесткости
Акустический шум	Диапазон частот, Гц Уровень звукового давления (относительно 2∙10^-5 Па) дБ	50-10000 130
Механический удар одиночного действия (для узлов крепления)	Пиковое ударное ускорение, м/с² (g) Длительность действия ударного ускорения, мс	147(15) 15
Линейное ускорение	Значение линейного ускорения, м/с²(g).	98(10)- 147 (15) - (для узлов крепления)
Атмосферное пониженное давление	Значение при эксплуатации, кПа (мм рт. ст.)	5,5 (41)
Пониженная температура среды	Рабочая, °С Предельная, °С	-40 -60
Повышенная температура среды	Рабочая, °С Рабочая, кратковременная,°С Предельная, °С	60 70 85
Повышенная влажность	Влажность относительная, предельная при температуре 35°С, %	98
Атмосферные конденсированные осадки (роса и внутреннее обледенение)	Пониженная температура, °С. Относительная влажность при температуре 35°С, не менее, % Пониженное давление, кПа (мм рт.ст.), не менее	-30 95 22,67(170)
Статическая пыль, (песок)	Скорость циркуляции, м/с, Концентрация, г/м³	0,5-1,0 3
Соляной (морской) туман	Водность, г/м³ Температура, °С Дисперсность не более, мкм	2-3 35 20
Плесневые грибы	Влажность повышенная, % Температура, °С	95-98 29

Сравнительный анализ ИБД представлен в таблице 2:

Таблица 2

Условное наименование	Диапазон измерений	Погрешность нуля пог- реш- ность коэффи- циента передачи	Рабочая температура	Габариты Вес	Исполнение	Производитель
IMU (инерциальный измерительный блок)	ω_X, ω_Y, ω_Z (3 ДУСа) 1000 гр/с (3 ДЛУ) n_x,y,z=50g	по ω 0.04%/σ, по n 0.2%/σ темп. стаб. нуля 5^О/час/ σ n=2mg/ σ (0.001%/ σ)	-40÷+75^О	75х56х40 250 г	моноблок модульный процессор, память УВВ, питание ±15В, +5В.	BAE System
ИБД	ω_X, ω_Y, ω_Z (18÷180⁰/с) n_x,y,z (1÷15g)	по ω ±1%, по n ±2%, нул. сигн. ≤1%	-60÷+60^ОС	2553 г (корпус 1330 г)	моноблок процессор, память УВВ. Питание 18÷31В п.т.	ОАО МНПК «Авионика»

Волоконный датчик ДУС в-5

Предназначен для измерения и контроля угловой скорости движущихся объектов.

Датчик является цельноволоконным вариантом кольцевого оптического интерферометра Саньяка, выполненного по сварной технологии и размещенного в герметичном корпусе.

Оптоволоконный ДУСв–5 , в котором отсутствуют вращающиеся гироскопы. Этот ДУС обладает существенно более высокой стабильностью (дрейф 15°/час), меньшим весом и габаритами.

Применение таких ДУСов, особенно более точных вариантов, может обеспечить не только нужды систем управления, но и нужды систем навигации.

Существуют датчики угловых скоростей:

- гироскопические (ДУС-35);

- на базе кремниевого чипа (чувствительный элемент на кольцевом микромеханическом вибрационном гироскопе);

- волоконно-оптические ДУСы на базе эффекта Саньяка (ДУСВ-5).

Достоинства и недостатки приведенных выше гироскопов:

Датчики угловых скоростей (ДУС гироскопические):

Недостатки:

- наличие вращающегося гироскопа;

- ограничение по сроку службы;

- трёхфазное напряжение питания гироскопа;

- габариты и вес велики;

- отсутствие кодового преобразования;

Достоинства:

- диапазон рабочих температур -60÷+60°С

ДУСы на базе кремниевых чипов с чувствительным элементом на кольцевом механическом вибрационном гироскопе

Недостатки:

- диапазон рабочих температур (-40÷+75°С);

- отсутствие кодового преобразования;

Достоинства:

- отсутствие вращающихся частей;

- отсутствие специальных источников питания;

- малый вес и габариты;

- возможность интегрального исполнения;

ДУСы волоконно – оптические на базе эффекта Саньяка

Недостатки:

- узок температурный диапазон;

- отсутствие кодового преобразования;

Достоинства:

- высокая чувствительность;

- высокая точность;

- отсутствие вращающихся гироскопов;

Корпус выполнен из алюминиевого сплава в виде цилиндрической призмы высотой 19,5 мм и диаметром 92 мм, имеет фланец с 4-мя отверстиями для крепления.

Является аналоговым преобразователем угловой скорости вращения в выходной электрический сигнал (напряжение). Выходное напряжение пропорционально угловой скорости и определяется как разность потенциалов между соответствующими контактами выходного разъема.

Начинает функционировать практически мгновенно после подачи всех напряжений. Последовательность подачи напряжений произвольная.

Отличается:

- малым весом и габаритами;

- быстрым запуском и выходом на рабочий режим;

- высокой чувствительностью;

- низким энергопотреблением;

- бесшумной работой;

- высокой надежностью;

- неограниченным количеством запусков;

- отсутствием погрешностей, присущих другим типам датчиков;

- устойчивостью к внешним воздействиям.

Структурно содержит в себе два основных модуля:

- чувствительный оптический модуль - волоконный оптический интерферометр включающий 100-метровый-чувствительный контур (катушку), два сварных волоконно-оптических ответвителя, волоконно-оптический поляризатор, пьезокерамический фазовый модулятор (ПЗТ), модуль суперлюминесцентного диода, фотоприемный модуль;

- электронный модуль - печатная плата, выполненная в технологии поверхностного монтажа, которая конвертирует сигнал оптического блока в напряжение, пропорциональное угловой скорости.

Технические характеристики:

Диапазон измеряемых скоростей, град/с +/-200

Рабочий диапазон частот 0 ... 1000 Гц

Ненулевой сигнал изделия, при отсутствии угловой скорости, не более ±1,0% от диапазона измерения.

Порог чувствительности не более 0,1 % от диапазона измерения. Нелинейность выходной характеристики не превышает:

при угловой скорости < 100°/сек 1 %

при угловой скорости > 100°/сек 20%

Вес, г 130

Время готовности не более, с 1

Напряжение питания, В ±12 ±0,6 / 5 ± 0,25

Средняя наработка на отказ, часов 15000

Ресурс, часов 25000

Срок службы, лет 25

Случайная составляющая ухода нулевого сигнала не более,°/час 5-15

Остаточный дрейф ДУСов представлен на рисунке 6:

Рисунок 6. Сравнительный анализ остаточного дрейфа ДУСов.

Сравнительный анализ Дусов представлен в таблице 4:

Таблица 4

Производитель	Гирооптика	Гирооптика	Analog Devices	Авионика
Тип	7ПСК(У)-360(1 )-027	ДУС-ММ-360	ADXRSЗОО	ДУСв-5
Диапазон измерения, град/с	±360	±360	±300	±200
Спектральная плотность случайной составляющей нулевого сигнала, град/с/√Hz	—	0,4	0,2	0,002
Нелинейность масштабного коэффициента, %	0,7	0,7	0,2	10-весь диапазон 2-половина диапазона
Стабильность нулевого сигнала, град/с	30	-	-	0,005
Нулевой сигнал, град/с	±15	-	-	±1
Дрейф нулевого сигнала, град/час	-	-	1000	15

Внешний вид ДУСв-5 представлен на рисунке 7:

Рисунок 7. Внешний вид ДУСв-5.

Датчики температуры

Параметры полупроводникового p-n перехода в биполярных диодах имеют температурную зависимость. Если прямосмещенный переход соединить с генератором постоянного тока, то его выходное напряжение будет находиться в прямо пропорциональной зависимости от температуры. Калибровка таких датчиков проводится только по двум точкам.

Три датчика температуры, расположенные на ДУСах имеют следующие параметры:

1. Выходное напряжение прямо пропорционально относительной температуре: 100мВ/°К.

2. Диапазон рабочих температур -55 +125 °С.

3. Номинальное значение тока питания 10мА.

3. Точность определения температуры +2°С.

Т,˚С	-50	-40	-30	-20	-10	0	+ 10	+20	+30	+40	+50
U,В	-5,180	-4,151	-3,103	-2,040	-1,010	0,000	1,021	2,063	3,156	4,178	5,22

VD1

Uвых = f(t˚C)

+ Uпит

Рисунок 8. Электрическая схема 1,2,3 датчиков температуры.

Четвертый датчик температуры работает по такому же принципу, но имеет другую схему (Рисунок 9).

На рисунке 10 представлена зависимость температуры от напряжения.

Рисунок 9. Электрическая схема 4-го датчика температуры.

-50

+50

T(˚C)

Рисунок 10. Зависимость температуры от напряжения

Цифровой вычислитель .

Вычислитель предназначен для обработки сигналов датчиков первичной информации, входящих в состав системы и ИБД, и передачи информации по независимому последовательному каналу в центральный вычислитель системы.

Состав цифрового вычислителя:

- Центральный процессор Л1867ВМ2 (тактовая частота 16МГц, производительность 4 млн. коротких операций в сек.) с 544 16-ти разрядными словами ОЗУ и таймером на кристалле,

- ПЗУ 128К 16-ти разрядных слов, реализованное на 2-х микросхемах FLASH памяти и распределенное по 64К слов в областях памяти программ и данных,

- 16 канальный буфер масштабных операционных усилителей, с «предцифровыми» фильтрами на входе АЦП,

- 16-ти канальное 12-ти разрядное АЦП с частотой обновления информации 2,5 кГц,

- Мультиплексный канал обмена по ГОСТ 26765.52-87 (форматы обмена 1,2,4) может работать в модах оконечное устройство и контроллер,

- Канал обмена по РТМ 1495-75 изм. 3,

- Порт ввода - вывода разовых команд (8-входных и 8-выходных разовых команд с ТТL уровнями),

- порт по RS-232,

- БОЗУ с организацией 2КХ16 в области "глобальной" памяти с косвенной адресацией,

- Пультовое устройство в состав которого входят:

1. Технологический последовательный канал RS-232

2. Программатор для ПЗУ

3. Сторожевой таймер

Предусмотрена в режиме "Регулировка" по внешней команде запись в ПЗУ нулевых значений сигналов датчиков.

Конструктивно вычислитель выполнен на многослойных печатных платах с применением элементов поверхностного монтажа, расположенных на двух сторонах печатной платы.

Блок питания

Входящий в состав ИБД блок питания предназначен для запитки вычислителя и датчиков, входящих в конструкцию, а также датчиков входящих в систему.

Блок питания вырабатывает следующие виды напряжений: (12±0,6)В, минус (12±0,6)В, (5±0,25)В, минус (5±0,25)В.

Пульсация напряжений не более 50 мВ.

Токи, потребляемые ИБД-43:

12В - не более 180 mА,

минус 12В - не более 220 mА,

5В - не более 1 А,

минус 5В - не более 50 mА.

Общая потребляемая мощность (при КПД - 75%):

[12Вх(0Д8+0,22)А + 5Вх(1,О+О,О5)А] /0,75 -13,4 Вт

При первичном напряжении 27 В, потребляемый ток составляет: 13,4Вт/27В = 0,5 А.

Моделирование БИНС

Схему построения БИНС поясним, рассмотрев типовой вариант конструкции трехканальной БИНС, представленный на рисунке 16. Первичные приемники информации в данном варианте – это 3 акселерометра и 3 датчика угловой скорости (ДУС),измеряющие соответственно проекции кажущегося ускорения и угловых скоростей на оси связанной системы координат. Акселерометры и ДУСы при монтаже на общей плате объединяются в интегральный блок датчиков (ИБД), в котором имеются еще 4 датчика внутренней температуры, таким образом, чтобы выполнялось условие:

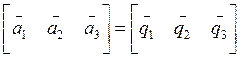
В свою очередь, интегральный блок датчиков жестко размещается на корпусе ЛА таким образом, чтобы связанный с его посадочными местами ортогональный базис совпадал с базисом связанной системы координат ССК.

Наличие блока ДУСов связано с решение задачи ориентации, а наличие блока акселерометров – с решением задач ориентации и навигации.

Рис. 16 Схема построения БИНС

Принцип работы БИНС заключается в построении расчетной системы координат, в которой интегрируются дифференциальные уравнения ориентации и навигации. Расчетная СК в БИНС реализуется аналитически, в отличии от платформенной ИНС, где она реализуется электромеханическими устройствами.

Алгоритм работы БИНС таков: с блока акселерометров и ДУСов в вычислитель подаются сигналы, несущие в себе информацию соответственно о проекциях кажущегося ускорения и проекциях угловой скорости на оси связанной СК. В вычислителе заложен алгоритм, по которому, исходя из полученных данных, рассчитываются навигационные параметры и параметры ориентации. А именно, координаты ЛА в земной СК (широта и долгота), восточная и северная составляющие скорости ЛА, ошибки измерения углов тангажа, крена и курса.

Заложенный в вычислитель алгоритм вычисления навигационных параметров для нашего случая выглядит так:

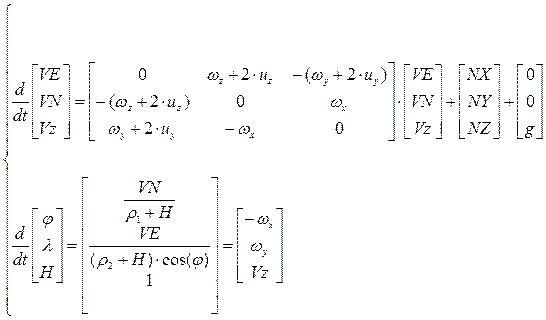(1)

где:

VE – восточная составляющая скорости ЛА;

VN – северная составляющая скорости ЛА;

φ – широта – координата местоположения ЛА;

λ – долгота – координата местоположения ЛА;

ωx, ωy, ωz – относительные угловые скорости земной СК.

uy, uz – проекции вектора угловой скорости вращения Земли на оси земной СК;

H – текущая высота полета;

NX, NY, NZ – проекции кажущегося ускорения на оси земной СК;

ρ1, ρ2 – соответственно минимальный и максимальный радиусы кривизны земного эллипсоида;

g – ускорение от силы тяжести.

Стоит отметить, что система 1 записана в форме Коши – удобном для дальнейшего интегрирования виде.

Радиусы кривизны земного эллипсоида определяются следующим образом:

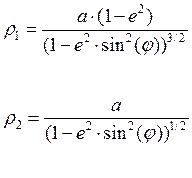
где:

а = 6378245 м – экваториальный полудиаметр (эллипсоид Красовского ПЗ-42);

e²= 0.0066934126 – эксцентриситет.

Проекции вектора вращения Земли определяются так:

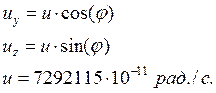
Относительные угловые скорости сопровождающего трехгранника находятся следующим образом:

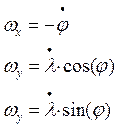
Как уже упоминалось, в данной модели фигурируют проекции кажущегося ускорения на оси сопровождающего трехгранника. А на вычислитель как исходные подаются проекции этих ускорений на оси связанной СК. Возникает вопрос перевода ускорений из связанной СК в земную. Для этого необходимо определить матрицу направляющих косинусов перехода. Так как мы решаем навигационную задачу в горизонтальной СК (земной), то матрица перехода в нее из связанной определяется решением обобщенного уравнения Пуассона вида:

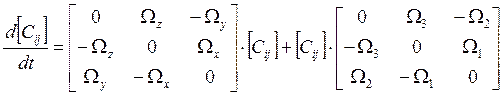(2)

где:

Ω_1,2,3 – измеряемые угловые скорости (проекции абсолютной угловой скорости вращения горизонтного трехгранника на оси связанной СК);

Ω_X_,_Y_,_Z – проекции абсолютной угловой скорости вращения горизонтного трехгранника на оси самого трехгранника. Эти элементы определяются следующим образом:

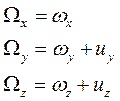
Также матрицу направляющих косинусов можно определить через углы курса, тангажа и крена ЛА:

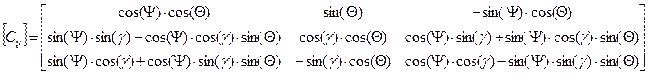
где:

Ψ – текущий угол курса;

γ – текущий угол крена;

θ – текущий угол тангажа.

Мы воспользуемся обоими вариантами, взяв первый за основной, а второй в качестве метода определения начальных значений элементов матрицы направляющих косинусов.

Итак, когда матрица перехода определена, мы можем перейти от связанной СК к земной:

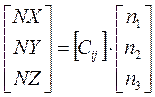
Итак, мы рассмотрели алгоритм расчета навигационных параметров, который реализован в вычислителе БИНСа. Но он является идеальным, так как мы нигде не учитывали ошибок. То есть это – идеальная модель БИНСа.

Для того, чтобы создать реальную модель, необходимо параллельно с идеальной моделью реализовать модель ошибок БИНС, которая имеет вид:

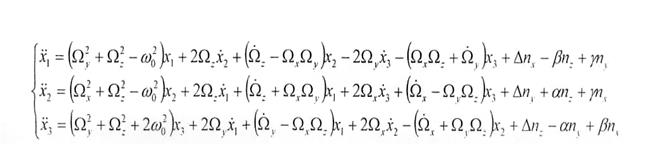
где:

x₁ – ошибка определения широты;

х₂ – ошибка определения долготы;

х₃ – ошибка определения высоты;

α, β, γ – соответственно ошибки определения углов курса, крена и тангажа. Наличие этих ошибок указывает на то, что расчетная СК БИНС не совпадает с сопровождающим горизонтным трехгранником.

Примем:

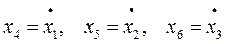
и приведем описанную модель ошибок к удобному для интегрирования виду – к форме Коши:

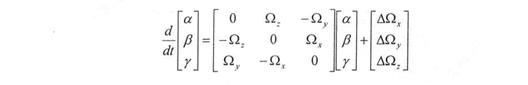
Обозначим эту систему 3. Здесь:

x₄ – ошибка расчета восточной составляющей скорости;

х₅ – ошибка расчета северной составляющей скорости;

х₆ – ошибка расчета вертикальной скорости.

ΔΩ_X_,_Y_,_Z – инструментальные ошибки ДУСов в проекциях на оси земной СК;

Δn_X_,_Y_,_Z – инструментальные ошибки акселерометров в проекциях на оси земной СК.

Приведенные инструментальные ошибки акселерометров и ДУСов определяются по формулам:

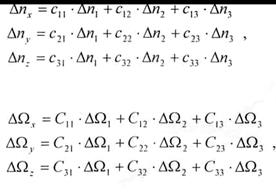
Здесь:

ΔΩ_1,2,3 – инструментальные ошибки ДУСов в проекциях на оси связанной СК (они задаются в описании приборов);

Δn_1,2,3 – инструментальные ошибки акселерометров в проекциях на оси связанной СК (они задаются в описании приборов).

Итак, подводя итоги данного раздела, надо сказать, что для проведения моделирования БИНС необходимо реализовать описанный выше алгоритм, решающий системы дифференциальных уравнений 1, 2 и 3.

Движение ЛА

При исследовании движения в различных режимах полета ЛА рассматривается как твердое тело, симметричное относительно основной плоскости связанной СК (вертикальной плоскости), на которое действуют аэродинамические силы и сила тяги, вектор которой находится в плоскости симметрии ЛА и проходит через центр масс ЛА. Таким образом, уравнения движения в векторной форме имеют вид:

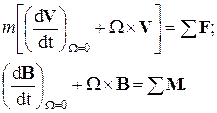(4)

где:

F- вектор сил, действующих на ЛА;

M- вектор моментов, действующих на ЛА;

B- вектор количества движения;

V- вектор линейной скорости;

W- вектор угловых скоростей;

m- масса ЛА.

При исследовании движения указанные векторы раскладываются на проекции по осям соответствующей системы координат (скоростной, связанной, экспериментальной и земной).

Поскольку имеют место дифференциальные уравнения, их необходимо привести к форме Коши, наиболее удобной для интегрирования:

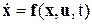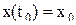
где:

x – вектор состояния;

u – вектор действующих факторов;

t – время.

Для формирования системы уравнений (4) в форме Коши, описывающей пространственное движение самолета используют уравнения динамики и кинематики движения центра масс самолета и уравнения динамики и кинематики движения самолета относительно центра масс.

Уравнения движения центра масс самолета в проекциях на оси скоростной системы координат имеют вид:

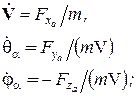(5)

где:

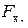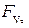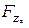, , - проекции результирующего вектора внешних сил (аэродинамической силы A, силы тяжести G) и тяги двигателей P на оси скоростной системы координат;

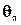- скоростной угол наклона траектории;

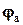- скоростной угол пути;

V- скорость самолета.

Кинематические уравнения движения центра масс ЛА в проекциях на оси земной СК могут быть записаны в виде:

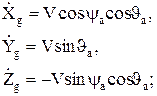(6)

где:

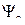- скоростной угол курса;

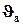- скоростной угол тангажа;

X_g, Y_g, Z_g- координаты самолета в земной системе координат.

Эти же уравнения, выраженные через основные углы имеют вид (7) :

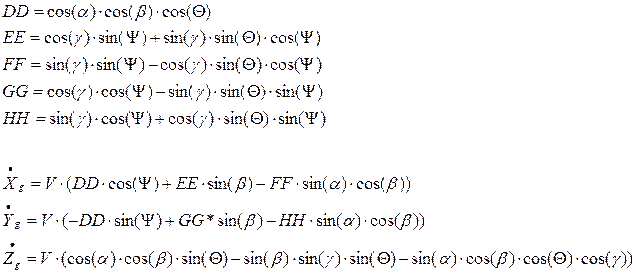
где:

DD, EE, FF, GG, HH – вспомогательные выражения для облегчения читаемости формул;

α – угол атаки;

β – угол скольжения;

γ – угол крена;

Ψ – угол курса;

Θ – угол тангажа.

Динамические уравнения движения самолета относительно центра масс записываются в форме:

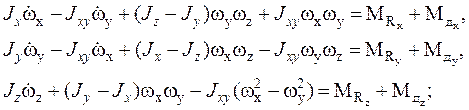(8)

где:

J_x, J_y, J_z- осевые моменты инерции самолета, заданные выше при описании параметров самолета;

J_xy- центробежный момент инерции самолета, заданный при описании параметров самолета;

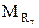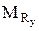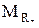, , - проекции результирующего момента аэродинамических сил M на оси связанной системы координат;

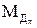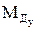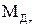, , - проекции момента дебаланса тяги двигателей M_Д на оси связанной системы координат;

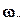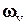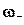, , - проекции вектора угловой скорости на оси связанной системы координат.

Для записи системы 8 в форме Коши необходимо из нее выделить производные проекций угловых скоростей:

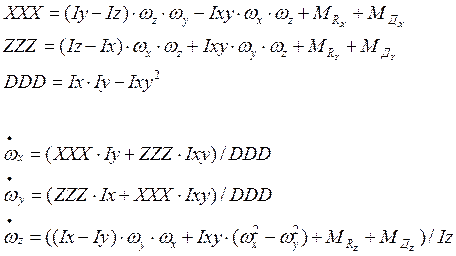(9)

Кинематические уравнения движения самолета относительно центра масс имеют вид:

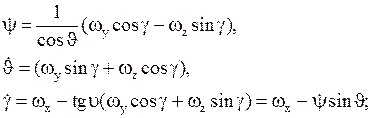(10)

где:

ψ- угол курса;

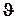- угол тангажа;

g- угол крена.

Изменение массы самолета происходит по следующему закону:

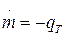(11)

где

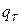- расход топлива,

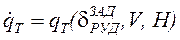Итак, для построения модели движения нашего самолета нам понадобятся системы дифференциальных уравнений 5, 7, 9, 10 и 11. Схема с уравнениями движения ЛА представлена на рисунке 17.

Аэродинамика

Аэродинамические силы и моменты могут задаваться в скоростной, связанной и экспериментальной системах координат. Мы будем использовать выражения в экспериментальной системе координат:

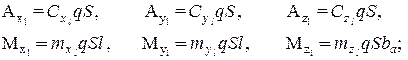(12)

где:

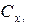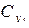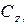, , -коэффициенты аэродинамических сил в экспериментальной системе координат;

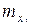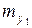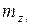, , - коэффициенты аэродинамических моментов в экспериментальной системе координат;

q – скоростной напор,

,
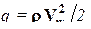r - плотность воздуха;

V_w- воздушная скорость;

S – площадь крыла самолета;
l – размах крыла самолета;

b_a- средняя аэродинамическая хорда крыла самолета; 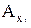, , 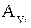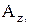- проекции аэродинамической силы на оси экспериментальной системы координат;

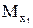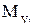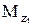, , - проекции аэродинамического момента на оси экспериментальной системы координат.

Коэффициенты аэродинамических сил и моментов зависят от многих параметров и определяются довольно громоздкими формулами. Подробнее о реализации аэродинамики самолета см. в приложении к пояснительной записке (в исходном коде программы и списке идентификаторов программы).

Модель ветра

В описании аэродинамики упоминалась воздушная скорость самолета. Она прямым образом зависит от наличия воздействия внешней среды (ветра). Это видно из формул:

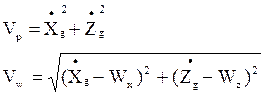
где:

Vp – путевая скорость самолета;

Vw – воздушная скорость самолета;

Wx, Wz – составляющие скорости ветра.

Как видно, при отсутствии ветра воздушная скорость влияния не имеет, так как вырождается в путевую.

Для учета воздействия внешней среды нам необходимо построить модель ветра и определить упомянутые выше скорости ветра и его ускорения. Определим их как порывы ветра турбулентной атмосферы с дисперсиями по составляющим равными 1 метр в секунду:

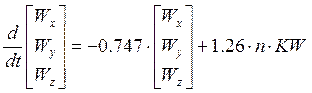(13)

где:

n – случайное число из набора случайных чисел [-1;1] с нормальным законом распределения;

KW = 8.6 – коэффициент, значение которого подобрано так, что дисперсии скорости ветра по составляющим = 1 метр в секунду.

Траектория полета

Поскольку мы разрабатываем модель движения ЛА, то необходимо задаться и вопросом – а куда и как собственно самолет летит!? Для решения этого вопроса необходимо построить и задать траекторию полета, движение ЛА на которой мы и будем моделировать.

Для простоты отладки модели зададим несложную траекторию, состоящую из трех участков:

Рисунок 18. Заданная траектория полета

Считаем, что первый участок полета – горизонтальный полет на Восток. Соответственно, третий участок – это полет на Север.

Для полноты задания траектории полета в модели движения ЛА необходимо задать такие параметры для каждого участка полета, как угол скольжения, крена, курса, угловые скорости по всем трем осям, угол наклона траектории.

Первый участок полета – горизонтальный полет. Так как с него начинается полет ЛА, то первым делом зададим скорость полета V0 = 230 м/с и высоту полета H0 = 11000 м, а также начальную массу ЛА M0 = 115000 кг. Так как полет горизонтальный то значит все проекции угловой скорости на оси связанной СК равны 0 рад./с. (ωx0 = 0, ωy0 = 0, ωz0 = 0). Углы скольжения и крена тоже зададим равными 0 рад. (β0 = 0, γ0 = 0). Угол наклона траектории GAM равен 0 рад. Поскольку на первом участке мы летим на Восток, то угол курса будет равен 90 град. (ψ0 = 90).

Второй участок полета – поворот на 90 град в течении 273 с. Значит угол крена имеет отличное от 0 значение. Зададим его равным 0.2 рад/с. Проекции угловой скорости на оси связанной СК ωy0 и ωz0 имеют такие значения, чтобы обеспечить поворот на 90 град. С заданным креном в заданное время. Эти значения рассчитываются следующим образом:

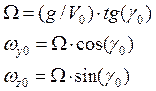
где: Ω – угловая скорость поворота.

Угол скольжения при повороте немного увеличивается и равен 0.02 рад. Угол наклона траектории GAM по прежнему равен 0 рад.

Третий участок полета – горизонтальный полет, как и первый участок. Соответственно, все параметры равны заданным на первом участке за исключением скорости, высоты (они задаются один раз в самом начале полета) и курса – так как теперь полет происходит на Север, то угол курса = 0 град.

Количество участков полета и их направление задается в полетном задании. Оно выглядит следующим образом и находится в папке \\PZ:

Полетное задание:

-----------------------------------

КORT=3 количество ортодромий

SX1 = 10000.0 длина ортодромии

PSIG1 = 0.0 рыскание ортодромии

SX2 = 10000.0 длина ортодромии

PSIG2 = 90.0 рыскание ортодромии

SX3 = 10000.0 длина ортодромии

PSIG3 = 0.0 рыскание ортодромии

По окончании программа выдает окно с результатами по времени, сколько было потрачено на каждый участок:

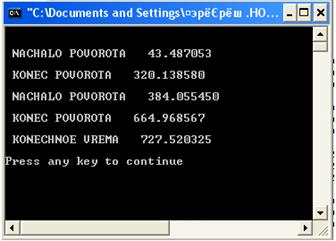
Балансировка

Балансировочные значения параметров самолета позволяют обеспечить выдерживание заданного режима полета при отсутствии возмущающих воздействий со стороны внешней среды. Эти значения определяют установившийся режим полета, когда силы и моменты, действующие на самолет, уравновешивают друг друга и обеспечивается его равномерное движение.

Отсюда следует, что балансировочные значения параметров самолета могут быть определены исходя из уравнений динамики, если приравнять в них нулю выражения, определяющие действующие на самолет ускорения.

При горизонтальном полете система трех нелинейных алгебраических уравнений содержит три неизвестных параметра, которыми являются тяга двигателей, угол атаки и отклонение руля высоты. Решением являются балансировочные значения этих параметров, которые обеспечивают установившееся движение самолета. Кроме того, в режиме поворота есть два дополнительных искомых параметра: отклонение руля элеронов и отклонение руля направления при заданной угловой скорости поворота.

Решение задачи поиска балансировочных параметров сводится к минимизации по искомым параметрам функции, образованной суммами квадратов правых частей решаемых нелинейных уравнений, которое осуществляется методом вращающихся координат.

Таким образом, при разработке модели движения ЛА по заданной траектории необходимо проводить балансировку самолета перед началом полета на каждом из участков траектории. В нашем случае нам необходимо три раза провести такие действия, так как мы задались траекторией, состоящей из трех участков.

Подробнее о поиске балансировочных параметров см. в приложении к данной пояснительной записке (в исходном коде программы).

Модель управления ЛА

Для полноты разрабатываемой модели полета ЛА нам необходимо реализовать модель его управления. Строго говоря, синтез законов управления – это довольно сложная вещь, которой отведена целая отрасль науки. Мы же ограничимся режимом стабилизации в качестве управления нашим самолетом. Назначением данного режима является автоматическая стабилизация углового положения летательного аппарата относительно заданного невозмущенного положения (балансировочного). По самому своему назначению это – режим малых отклонений, при котором обычно можно использовать линейные модели (линейные уравнения) объекта управления.

В рамках рассматриваемого режима стабилизации продольное и боковое движения являются независимыми, автономными. Ясно, что критерии оптимальности – функционалы для этих движений должны быть независимыми, т. е. содержащими автономные группы фазовых координат и управлений. Оптимальные управления при этом получаются также независимыми и могут синтезироваться путем решения двух автономных задач.

В рассматриваемой полной линейной модели продольного движения отклонения скорости полета и угловые отклонения взаимосвязаны. Поэтому синтез собственно автопилота-стабилизатора углового положения в строгой постановке должен осуществляться одновременно с синтезом стабилизатора скорости (автомата тяги).

Стабилизация для контуров продольного движения:

Для контуров стабилизации продольного движения немаловажную роль играет инерционность исполнительных устройств. Для краткости ограничимся простейшими линейными моделями исполнительных устройств в виде апериодических звеньев:

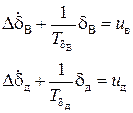
Для рассматриваемого самолета принят следующие закон управления на указанном маршруте:

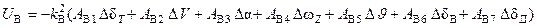
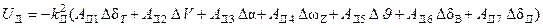
где:

Ui – синтезируемые управления ( );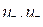

Ki , Aij –постоянные положительные коэффициенты;

Δ – отклонение параметров состояния.

Датчики 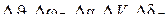будем считать безинерционными.

Рассмотрим теперь задачу синтеза контуров стабилизации крена, рысканья и скольжения, т. е. задачу синтеза системы стабилизации бокового движения.

Стабилизация для контуров бокового движения:

Уравнении исполнительных устройств канала элеронов и канала руля направления:

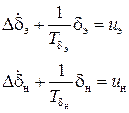
Для рассматриваемого самолета принят следующие закон управления на указанном маршруте:

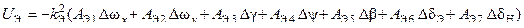
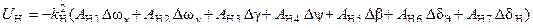
где:

Ui – синтезируемые управления;

Ki , Aij –постоянные положительные коэффициенты;

Δ – отклонение параметров состояния.

Подробно написанные режимы стабилизации для всех контуров см. в приложении к данной пояснительной записке (в исходном коде программы).

Итак, рассмотрев все аспекты и проблемы создания модели полета ЛА по заданному маршруту, можно сделать следующий вывод: для реализации такой общей модели необходимо в совокупности решить уравнения 5, 7, 9, 10, 11, учитывая аэродинамику ЛА (12), воздействие внешней среды (13), балансировку ЛА на каждом участке маршрута и принятые законы стабилизации.

Алгоритм моделирования

В рамках данной работы необходимо разработать программное обеспечение (программный продукт), который будет в комплексе реализовывать все рассмотренные выше математические модели.

Такой программный продукт (ПП) был разработан средствами оговоренного выше языка программирования. Он получил название СКМ.DSP. Компакт-диск с программой (СКМ.DSP), ее описанием, полным проектом в Visual C++ и всей документацией приложен к данной пояснительной записке.

В программе учтены все рассмотренные модели, а интегрирование проводилось численным методом Рунге-Кутта 4 порядка с постоянным шагом интегрирования. Поскольку на сегодняшний день программирование приняло объектно-ориентированный вид, то при разработке ПП тоже использовался такой подход, и все рассмотренные модели сделаны в виде отдельных функций; также написана основная функция моделирования, которая управляет взаимодействием всех остальных функций.

Перечень всех основных функций и их описаний приведен в таблице 12 (в связи с громоздким синтаксисом функций в таблице представлены упрощенные варианты, дающие общее представление о функции). Для подробного ознакомления с синтаксисом программы см. приложение к данной пояснительной записке (исходный код программы):

Таблица 12

№	Функция	Описание
1	AISB ( )	Функция реализует алгоритм инициализации состояния борта
2	AIVSO ( )	Функция реализует алгоритм инициализации вектора состояния объекта
3	AZPZ ( )	Функция реализует алгоритм загрузки полетного задания
4	DISPBAL ( )	Функция реализует диспетчер процедур расчета балансировочных параметров
5	HORIZBAL ( )	Функция, реализующая процедуры расчета балансировочных параметров при горизонтальном полете
6	TURNBAL( )	Функция, реализующая алгоритм расчета балансировочных параметров при повороте
7	DISPCKM ( )	Функция, реализующая диспетчер моделирующего комплекса
8	RK4 ( )	Функция реализующая алгоритм интегрирования методом Рунге-Кутта 4 порядка
9	AEROFLU ( )	Функция, реализующая аэродинамику объекта (расчет коэффициентов аэродинамических сил и моментов)
10	OBEKT ( )	Функция, реализующая модель пространственного движения объекта
11	AFUVRO ( )	Функция, реализующая модель автопилота (законы стабилизации), алгоритмы формирования управляющих воздействий на рулевые органы
12	AONP ( )	Функция, реализующая алгоритм определения навигационных параметров
13	ARVP ( )	Функция, реализующая алгоритм расчета требуемых (выдерживаемых законом управления) параметров
14	SREDA( )	Функция, реализующая модель воздействия ветра
15	TLM ( )	Функция, реализующая алгоритмы записи параметров состояния в файлы телеметрии
16	AIUUS ( )	Функция, реализующая алгоритм измерения ускорения и угловой скорости
17	COMMON ( )	Функция, содержащая функции общего назначения
18	PAR( )	Функция, содержащая все глобальные идентификаторы
19	PKS (), WRK50()	Функции, реализующие в совокупности минимизацию заданной функции методом вращающихся координат и поиск балансировочных параметров при горизонтальном полете
20	FCT	Функция, возвращающая сумму квадратов правых частей уравнений для балансировки
21	FORMDYT (), DEFORMDYT ()	Функции, реализующие алгоритмы формирования/деформирования вектора интегрируемых параметров
22	AMIN ()	Функция, реализующая алгоритм сравнения 2х чисел и выбора наименьшего
23	AMAX ()	Функция, реализующая алгоритм сравнения 2х чисел и выбора наибольшего
24	Matrixmult ( )	Функция реализует произведение двух матриц размерностями до 3х3
25	MatrixSum ()	Функция реализует процедуру сложения 2х матриц 3х3
26	CHANCE ()	Функция реализует процедуру формирования случайных чисел с нормальным законом распределения и СКО = 1.0
27	Generator ()	Функция реализует процедуру - генератор случайных нормальных распределений чисел в интервале [-1;1]

Рассмотрев все основные функции, теперь мы можем наглядно представить алгоритм работы программы. Он представлен в виде блок-схемы на рисунке 6. Отметим, что в представленном алгоритме опущены второстепенные функции типа AMIN,… в связи с тем, что схема получится слишком нагроможденной.

I. ВВЕДЕНИЕ

II. РАСЧЕТНАЯ ЧАСТЬ

Задачи автоматического управления на всех этапах полета. Законы управления КСУ.

Режимы полета успешно реализованы на многих самолетах как военного, так и гражданского применения. При разработке законов управления системы управления целесообразно применить методику, широко используемую при проектировании САУ для пилотируемых ЛА, а именно, движение ЛА рассматривается раздельно в вертикальной (продольное движение) и горизонтальной (боковое движение - движение крена-рыскания) плоскостях, и соответственно редуцируются уравнения движения ЛА. Ниже приводятся возможные варианты алгоритмов решения этих задач.

Для управления продольным движением ЛА возможно применить в качестве внутренних контура стабилизации либо утла тангажа, либо нормальной перегрузки, обладающие каждый определенными достоинствами:

- контур стабилизации угла тангажа дает возможность непосредственного управления угловым положением ЛА (заданного в техническом задании (ТЗ)), а управление ЛА в пределах допустимых значений нормальной перегрузки, ограниченных требованиями ТЗ, обеспечивается соответствующим качеством управления (при этом компромиссно недоиспользуются маневренные возможности ЛА), либо введением в контур специальных ограничителей нормальной перегрузки,

- контур управления нормальной перегрузкой обеспечивает использование всех маневренных возможностей ЛА (возможен выход непосредственно на предельные значения нормальной перегрузки), а режим управления и стабилизации угла тангажа опосредован через управление нормальной перегрузкой.

Оба контура дают возможность обеспечить достаточно качественное управление траекторией полета ЛА.

Для управления боковым движением ЛА (контура крена-рыскания) весь процесс управления сосредоточивается в канале управления углом крена, а капал рыскания автономно работает в режиме демпфера, если собственного демпфирования движения рыскания свободного ЛА не хватает. Для обеспечения хорошей координации движения крена-рыскания пилотируемого ЛА необходимо, чтобы собственное демпфирование движения рыскания имело декремент затухания ζр > 0,2 (повидимому, для беспилотного ЛА это требование можно несколько ослабить примерно до ζр = 0.15, а, может быть, и еще меньше - это является предметом специального исследования).

Такой принцип построения системы управления боковым движением ЛА самолетной конфигурации достаточно хорошо проработан и дает хорошие результаты. Он обеспечивает хорошее качество управления траекторией полета ЛА как в горизонтальной плоскости, так и в процессе набора высоты и снижения ЛА во всех режимах работы.

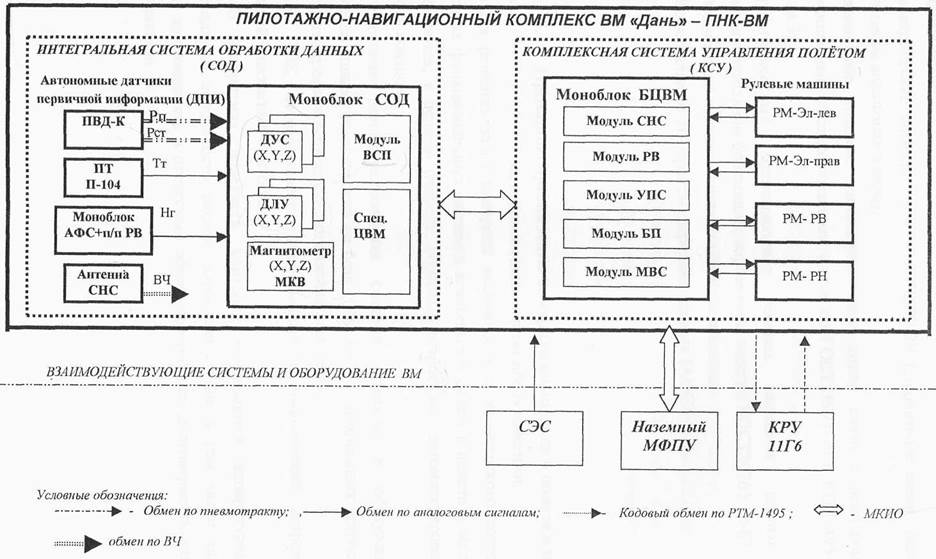
КСУ входит в состав пилотажно-навигационного комплекса. Это показано на рис.1. Описание интегрального блока датчиков (ИБД) приведено ниже, остальных, входящих в ПНК блоков описание приведено в Приложении.

Появилась возможность на базе ИБД создавать комплексные системы автоматического управления, обеспечивающие в простых и сложных метеоусловиях, на любых географических широтах, в любое время суток: автоматическое определение координат центра масс управляемого объекта и углов ориентации собственных осей объекта относительно заданной системы координат; управление и стабилизацию движения на маршруте и конечном участке траектории с цифровым управлением блоком электрических рулевых приводов непосредственно от вычислителя, входящего в состав ИБД.

Основные задачи, решаемые КСУ можно сформулировать следующим образом:

- наземный и предпусковой контроль технического состояния аппаратуры КСУ, выявление и диагностика неисправностей;

- автоматизированный ввод полетного задания перед пуском;

- выставка;

- определение навигационных параметров и углов ориентации в заданной системе координат (реализация алгоритма БИНС) в режиме без спутниковой коррекции (возможность обработки сигналов от спутниковой навигационной системы (СНС) имеется);

- управление полетом ЛА в автономном режиме в соответствии с полетным заданием;

- автоматический переход на режим пикирования на конечном участке траектории и осуществление распаковки.

Блок ИБД

Рисунок 1. Архитектура пилотажно-навигационного комплекса.

Дата: 2019-04-23, просмотров: 598.

12 3 4 5 6 7 8 9 10 Следующая ⇒