Формирование модели начинают с составления расчетной схемы, в которую включают существующие узлы и ветви, новые узлы и возможные дополнительные трассы линий, связывающих их с существующими объектами системы. Здесь должны учитываться и те линии, которые были найдены в результате анализа модели по выбору структуры генерирующих мощностей. Расчетная схема должна быть разумно избыточной и включать дополнительные линии, так чтобы не пропустить возможные оптимальные связи.
Для узлов должны быть заданы прогнозируемые нагрузки и мощности вводимых блоков. Таким образом, расчетная схема будет иметь 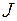 расчетных узлов, из них
расчетных узлов, из них 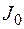 – существующих; т.е. индекс узлов
– существующих; т.е. индекс узлов 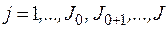 . Аналогично число ветвей в расчетной схеме
. Аналогично число ветвей в расчетной схеме 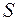 , из которых
, из которых 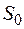 – существующих.
– существующих.
В качестве неизвестных можно принять потоки активной мощности по ветвям 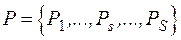 .
.
В качестве целевой функции рассмотрим затраты в существующие линии, пропорциональные потерям энергии, и в новые линии, определяемые в соответствии с принятыми аппроксимирующими выражениями З(Р) для удельных затрат:
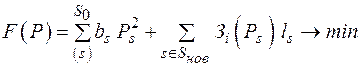 ,
,
где 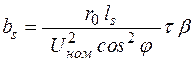 .
.
На неизвестные потоки мощности по ветвям накладывается условие баланса мощностей в узлах, которое может быть записано в матричной форме:
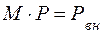 .
.
Здесь 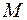 – прямоугольная матрица соединений узлы-ветви, причем ее элементы для узла j и ветви s обозначаются
– прямоугольная матрица соединений узлы-ветви, причем ее элементы для узла j и ветви s обозначаются 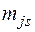 и могут принимать значения, равные 1, если ветвь выходит из узла; +1, если ветвь входит в узел и 0, если она не связана с узлом.
и могут принимать значения, равные 1, если ветвь выходит из узла; +1, если ветвь входит в узел и 0, если она не связана с узлом.
Таким образом, задача выбора оптимальной схемы сети заключается в поиске минимума некоторой нелинейной функции 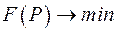 при соблюдении линейного ограничения в форме равенства
при соблюдении линейного ограничения в форме равенства 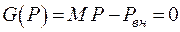 .
.
Сформулированная таким образом задача планирования развития сети сводится к задаче нелинейного программирования. Эта задача, как правило, имеет один экстремум. Для решения её могут использоваться известные методы нелинейного программирования.
Учет затрат в ЛЭП
Затраты в ЛЭП определяются сечением, типом опор и передаваемой мощностью. При планировании заранее не известно сечение ЛЭП, следовательно, затраты в линию необходимо представить функцией только от ее потока мощности, исключив сечение, но сохранив возможность определения сечения по найденному в результате решения модели потоку. Для этой цели может использоваться известный метод экономических интервалов. Рассмотрим суть этого метода.
Затраты на 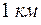 ЛЭП определенного типа и i-го сечения можно определить как приведенные затраты:
ЛЭП определенного типа и i-го сечения можно определить как приведенные затраты:
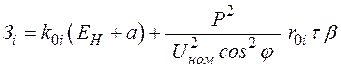 ,
,
где 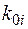 – удельные затраты;
– удельные затраты;
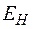 – нормативный коэффициент;
– нормативный коэффициент;
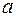 – коэффициент амортизационных отчислений;
– коэффициент амортизационных отчислений;
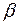 – стоимость потерянной электроэнергии,
– стоимость потерянной электроэнергии,
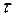 – число часов набольших потерь.
– число часов набольших потерь.
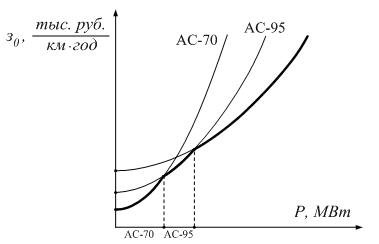
Рисунок 1
Если построить зависимости для всех сечений, допустимых для принятого напряжения 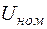 , то получим семейство пересекающихся парабол. На рисунке 1 показаны только 3 сечения ЛЭП 110 кВ.
, то получим семейство пересекающихся парабол. На рисунке 1 показаны только 3 сечения ЛЭП 110 кВ.
По нижней огибающей удельных затрат можно составить выборку и использовать ее для аппроксимации для принятого предиктора методом наименьших квадратов.
3. Применение метода проектирования градиента
Как известно, основное уравнение градиентного метода при безусловной оптимизации:
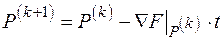 .
.
Здесь P – вектор переменных, F ( P ) – целевая функция, k – номер итерации, t – шаг.
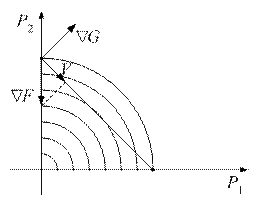
Рассмотрим простейший пример, в котором необходимо выбрать сеть для питания только одного узла (рисунок 2). Полагаем, что затраты представлены квадратичными зависимостями. В качестве исходной точки примем Р0=(0,РН).
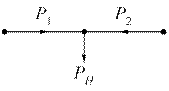
| 
|
Рисунок 2
При учете ограничений движение к минимуму должно осуществляться по проекции градиента на поверхность ограничений, т.е. вдоль вектора V . Вектор V можно получить путем исключения из 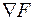 составляющих, перпендикулярных поверхности ограничений. Эти составляющие образуют градиент ограничений
составляющих, перпендикулярных поверхности ограничений. Эти составляющие образуют градиент ограничений 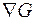 . Таким образом, вектор V определяется по выражению
. Таким образом, вектор V определяется по выражению
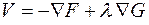 .
.
Для определения неопределенных множителей 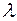 , образующих вектор V, используется условие равенства нулю скалярного произведения:
, образующих вектор V, используется условие равенства нулю скалярного произведения:
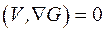 .
.
Из этого условия, приняв для линейного ограничения градиент равным 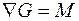 , можно найти
, можно найти 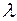 . Действительно, из преобразования
. Действительно, из преобразования
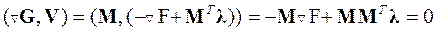
можно получить следующее матричное выражение для множителей 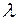
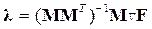 .
.
Составляющие вектора множителей λ позволяют определить все составляющие вектора V
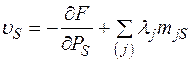 ,
,
и использовать их в процедуре градиентного метода
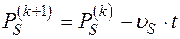 .
.
Определить проекцию градиента V можно, если использовать полученное выше матричное выражение для λ и провести следующее преобразование
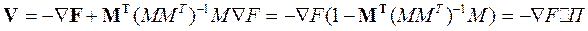 ,
,
где П= 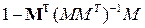 - матрица проектирования.
- матрица проектирования.
Итерационный процесс начинается с выбора исходного приближения и продолжается до тех пор, пока не выполнится условие требуемой точности для всех составляющих 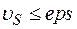 .
.
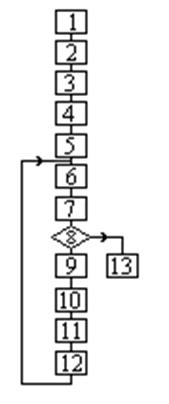
| Блок-схема алгоритма с выбором оптимального шага приведена на рисунке. Назначение блоков:
1. Формирование расчетной схемы.
2. Определение типа функций для расчета затрат и их
производных для всех ветвей.
3. Формирование матрицы инциденций М.
4. Определение матрицы проектирования градиента П.
5. Исходное приближение потоков Р=Р0.
6. Вычисление градиента 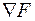 в точке Р.
7. Определение проекции V градиента.
8. Проверка условия окончания в точке Р.
7. Определение проекции V градиента.
8. Проверка условия окончания 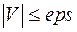 .
9. Организация пробного шага Р1= Р- V t 0/ .
10. Вычисление градиента и проекции V1 в конце шага.
11. Определение оптимального шага .
9. Организация пробного шага Р1= Р- V t 0/ .
10. Вычисление градиента и проекции V1 в конце шага.
11. Определение оптимального шага
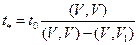 .
12. Рабочий шаг .
12. Рабочий шаг 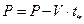 .
13. Вывод результатов .
13. Вывод результатов
|
Объект исследования
В качестве объекта исследования принята проектируемая сеть 110 кВ, расчетная схема которой представлена в виде графа сети на рисунке 3. Нагрузки в узлах, длины возможных ЛЭП приведены в таблице.
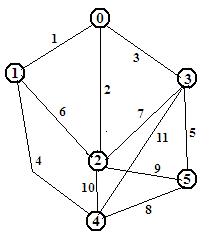
Рисунок 3
Таблица 1
| № | Длины ЛЭП, км | Нагрузки, МВт | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 1 | 2 | 3 | 4 | 5 | |
| 1 | 30 | 40 | 25 | 28 | 30 | 30 | 40 | 25 | 30 | - | - | 35 | 45 | 25 | 15 | 15 |
| 2 | 28 | 35 | 40 | - | 28 | 30 | 30 | 40 | 25 | 30 | - | 42 | 27 | 31 | 18 | 20 |
| 3 | 20 | 45 | 35 | - | - | 28 | 30 | 30 | 40 | 25 | 30 | 28 | 33 | 39 | 22 | 18 |
| 4 | 40 | 35 | 30 | 28 | 30 | 30 | - | 28 | 30 | 35 | - | 30 | 50 | 20 | 15 | 20 |
| 5 | 30 | 40 | 25 | - | 28 | 30 | 30 | - | 28 | 30 | 35 | 35 | 40 | 25 | 18 | 15 |
| 6 | 28 | 35 | 40 | - | 40 | 28 | 30 | 30 | - | 35 | 40 | 42 | 27 | 35 | 18 | 22 |
| 7 | 20 | 45 | 35 | 30 | 35 | - | 30 | 35 | - | 30 | 35 | 28 | 30 | 39 | 25 | 18 |
| 8 | 40 | 35 | 30 | 42 | - | - | 35 | 28 | 30 | 24 | 32 | 30 | 40 | 20 | 15 | 22 |
Исследование проводится с использованием программы, фронтальная панель которой показана на рисунке 4. В верхней части расположены приборы для ввода исходной информации по сети: количества узлов Ny и ветвей Nv, матрицы соединений М, вектора исходного приближения потоков по ветвям Ро, вектора коэффициентов градиента затрат по ветвям сети dF, пробного шага to и точности eps.
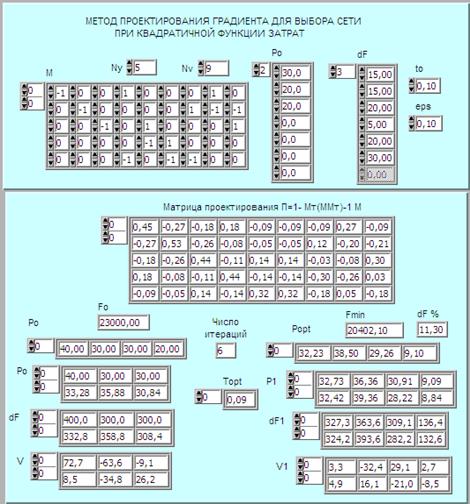
Рисунок 4
В нижней половине показаны результаты работы алгоритма оптимизации: матрица проектирования, исходные потоки по ветвям и общие затраты, число итераций и потоки по ветвям в оптимальной схеме. Ниже в массивах выведены для всех итераций текущие значения потоков Po , градиента dF и его проекции V, а также их значения в конце пробного шага, т.е. потока P1, градиента dF1 и проекции V1. Выведены и значения оптимального шага на итерациях
Чтобы посмотреть эти результаты надо на верхнем цифровом индикаторе номера элемента (строки) установить номер итерации, а на нижнем номер ветви, с которой начинается зона вывода. При этом нумерация начинается с нуля.
Для любознательных, знакомых с основами программирования в среде LabVIEW, на рисунке 5 показана программа оптимизации, написанная на языке графического программирования LabVIEW.
Порядок выполнения работы
1. Построить зависимости удельных затрат для ЛЭП 110 кВ. Стоимость 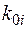 для выбранного типа линий принять по справочнику, нормативный коэффициент Ен=0,15; коэффициент амортизационных отчислений а=0,1; стоимость потерянной электроэнергии в руб/кВт*ч принять
для выбранного типа линий принять по справочнику, нормативный коэффициент Ен=0,15; коэффициент амортизационных отчислений а=0,1; стоимость потерянной электроэнергии в руб/кВт*ч принять 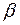 =2+0,1*№, Тм=5000 ч., cos=0,9.
=2+0,1*№, Тм=5000 ч., cos=0,9.
2. Определить экономические интервалы для всех сечений.
3. Составить выборку по нижней огибающей затрат и методом наименьших квадратов найти коэффициенты предиктора З=а+в Р2 .
4. Для заданной схемы сети ввести сплошную нумерацию ветвей, начиная с дерева, выбрать положительные направления ветвей и составить матрицу М. Определить исходное приближение Ро потоков, приняв в качестве его потокораспределение в дереве.
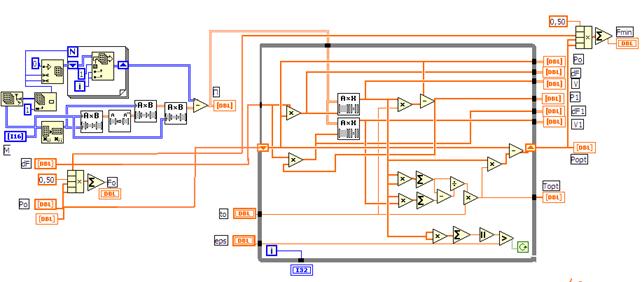 Рисунок 5
Рисунок 5
5. Определить коэффициенты в составляющих градиента для упрощенной целевой функции
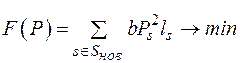 .
.
6. Активизировать программу Gradient . exe или Gradient . vi . Ввести исходные данные.
7. Для одной из ветвей построить графики итерационного процесса, т.е. отобразить изменение потока Po , градиента dF и его проекции V, а также значений в конце пробного шага P1, dF1 и V1.
8. Определить сечение ЛЭП по методу экономических интервалов.
9. Оценить возможности учета коэффициента а предиктора затрат в алгоритме выбора сети.
Контрольные вопросы
1. В чем смысл градиентного метода?
2. Для чего применяется проектирование градиента?
3. Как учитывается конфигурация сети?
4. Дерево и хорды в схеме сети
5. Как определить число деревьев в схеме.
6. Метод экономических интервалов и его применение.
7. Суть метода ветвей и границ для выбора сети.
Лабораторная работа N 6
ПАРАМЕТРЫ РЕЖИМА ЭНЕРГОСИСТЕМЫ
Цель работы: исследование параметров режима энергосистемы и разделение их на независимые и зависимые с оценкой влияния на критериальные функционалы, определяющие экономичность режима.
1. Общие сведения
Режимом энергосистемы называется некоторое состояние ее, определяемое значениями расхода топлива, давления и температуры пара на ТЭС, напора и расхода воды на ГЭС, частоты, напряжения токов, мощностей и других физических величин, называемых параметрами режима, которые характеризуют процесс производства, передачи, преобразования и распределения электрической энергии. Параметры режима делятся на технологические и электрические.
Стационарный режим электрической системы при известных параметрах системы, определяемых составом включенного в работу оборудования и его техническими характеристиками, описывается системой нелинейных алгебраических уравнений, обычно узловых
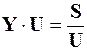 , (1)
, (1)
где Y – матрица узловых проводимостей, U – вектор узловых напряжений,
S – вектор узловых мощностей.
При заданных мощностях Si всех узлов кроме балансирующего и напряжении Uo в этом узле решение системы позволяет найти все остальные узловые напряжения. Для решения могут использоваться различные итеративные и прямые методы. Полученные напряжения позволяют определить любые интересующие параметры режима: потоки и токи ветвей, фазовые углы векторов напряжений, потери в сети, расход топлива на ТЭС и т.п.
Узловые мощности и Uo относятся к независимым параметрам режима, Мощности нагрузочных узлов определяются потребителями электроэнергии и в нормальных ситуациях должны быть обеспечены режимом энергосистемы. Мощности генерирующих узлов могут меняться по заданию диспетчера энергосистемы с целью обеспечения требований надежности, качества и оптимальности режима. В энергосистемах, где электрическая сеть имеет разные номинальные напряжения и автотрансформаторы связи, диспетчер может влиять на режим путем изменения их коэффициентов трансформации К. Диспетчер, наконец, может изменять также и состав включенного в работу оборудования (блоков на электростанциях, ЛЭП и автотрансформаторов).
Таким образом все множество электрических параметров режима можно разделить на следующие группы.
1. Узловые нагрузки Pi, Qi, которые являются заданными.
2. Мощности источников Pj, Qj, напряжение в балансирующем узле Uo, коэффициенты трансформации К, которые подвластны диспетчеру энергосистемы. Их назовем независимыми параметрами режима и объединим в вектор X. В качестве своеобразного независимого параметра можно рассматривать и состав включенного в работу оборудования.
3. Все остальные параметры режима, которые являются зависимыми и образуют вектор Y.
В задаче оптимизации режима составляющие xi вектора X определяются по условию минимума затрат на топливо или, в отдельных подзадачах, минимума потерь в сети. При этом поиск оптимального режима должен проводиться в области допустимых режимов, определяемой условиями надежности и качества.
При исследовании на ЭВМ реализованная имитационная модель режима электрической системы строится на использовании метода Ньютона первого порядка. С этой целью на основе (1) формируется вектор-функция небалансов узловых токов
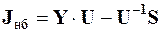 . (2)
. (2)
Действительные и мнимые составляющие тока небаланса для i-го узла будут
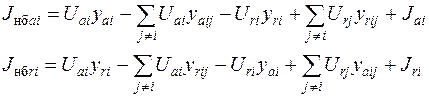 (3)
(3)
По методу Ньютона функция небаланса заменяется разложением в ряд Тейлора в точке с текущим значением U=Uo :
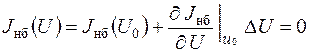 , (4)
, (4)
откуда определяется приращение напряжения
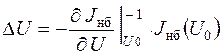
и основное уравнение итерационного процесса
Метод Ньютона имеет хорошую сходимость.
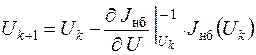 .
.
Объект исследования
Все исследования проводятся для энергосистемы, расчетная схема которой показана на рис.1. В системе 7 независимых узлов, в том числе 4 нагрузочных и 3 генерирующих (2 КЭС и 1 СК), 10 ветвей, в том числе 2 АТ и 2 двухцепных ЛЭП. В качестве балансирующего приняты шины 220 КВ соседней системы. На схеме приведены сопротивления ветвей и величины заданных параметров режима. Для ветвей указаны принятые положительные направления потоков.
Вектор независимых параметров режима ограничен и включает Uo - напряжение в балансирующем узле, P1 и Р2– активную мощность КЭС, Q1, Q2 –реактивную мощность КЭС, K1 - коэффициент трансформации АТ-1, Qск - мощность синхронного компенсатора. Предусмотрена возможность изменения состава оборудования.
3. Программное обеспечение
Лабораторная работа проводится с использованием программы ACYLB1.exe.
После вызова программы проводится расчет режима исследуемой системы при исходных значениях независимых параметров режима, которые устанавливаются на виртуальных потенциометрах независимых параметров режима. Расход топлива и потери в сети отображаются снизу в левой части экрана.
Рекомендуемые ограничения независимых параметров режима:
40 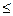 Р
Р 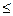 90, 10
90, 10 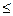 Q
Q 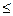 50, 0
50, 0 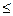 Qск
Qск 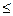 50, 210
50, 210 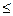 Uo
Uo 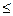 230, 0.45
230, 0.45 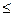 K1
K1 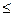 0.55.
0.55.
Порядок выполнения работы
1. Запустить программу и выставить расчетный режим в соответствии с вариантом (таблица 1). Для этого поочередно выставлять заданные значения независимых параметров в любой последовательности. Все дальнейшие исследования проводятся для установленного режима.
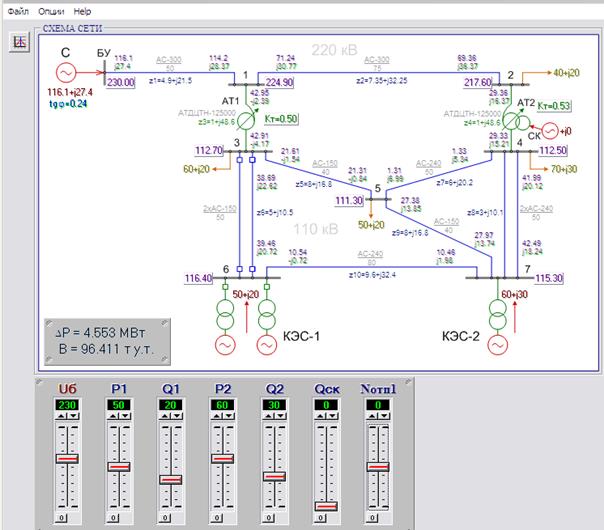
Рис 1. Схема исследуемой энергосистемы
Таблица 1.
| № | Р1 | Q1 | К | P2 | Q2 | Uo |
| 1 | 0 | 20 | 0,50 | 50 | 40 | 215 |
| 2 | 10 | 30 | 0,52 | 45 | 30 | 220 |
| 3 | 20 | 40 | 0,54 | 30 | 20 | 223 |
| 4 | 30 | 50 | 0,48 | 35 | 20 | 228 |
| 5 | 40 | 60 | 0,46 | 20 | 30 | 218 |
| 6 | 50 | 70 | 0,50 | 25 | 20 | 216 |
| 7 | 15 | 40 | 0,52 | 30 | 25 | 218 |
| 8 | 25 | 30 | 0,53 | 40 | 35 | 215 |
2. Построить зависимости потерь dP, расхода топлива B, напряжения в узле i и потока P+ jQ в ветви s от независимых параметров режима, определенных преподавателем.
3. Оценить влияние состава работающего оборудования на режим системы.
4. Определить производные потерь, называемые удельными приростами, в расчетном режиме по независимым параметрам методом конечных приращений.
5. Определить удельный прирост расхода топлива методом конечных и центрированных приращений. Оценить погрешность метода.
6. Определить оптимальное значение К1 без учета и с учетом заданных ограничений. Построить зависимость уравнительного потока от К.
7. Методом покоординатной оптимизации провести комплексную оптимизацию режима и оценить эффект.
8. Все результаты исследований представить в отчете.
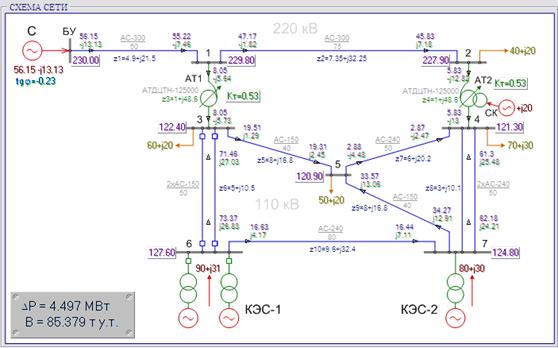
Рис. 2. Исходный режим энергосистемы
Контрольные вопросы
1. Какие параметры режима относятся к независимым ?
2. Что входит в вектор зависимых параметров режима?
3. Критерии оптимизации для поиска оптимальных значений различных параметров режима.
4. Назовите некоторые ограничения, которые необходимо учитывать при оптимизации.
5. Как учитывается конфигурация сети в узловом уравнении ?
6. Как влияет изменение коэффициента трансформации АТ на расход топлива в системе?
7. Как влияет изменение состава включенного оборудования на режим энергосистемы?
Лабораторная работа N 7
КОМПЛЕКСНАЯ ОПТИМИЗАЦИЯ РЕЖИМА ТЭС В СИСТЕМЕ
Цель работы : Исследование критериев и методов комплексной оптимизации режима теплоэнергетической системы и оценка эффекта от оптимального распределения активной и реактивной нагрузки.
Общие сведения
Задача комплексной оптимизации режима энергосистемы заключается в поиске такого распределения активных и реактивных мощностей между источниками при котором обеспечивается минимальный расход топлива на тепловых станциях для каждой ступени суточного графика.
| Рассмотрим энергосистему, в которой можно выделить одну ТЭС, работающую через сеть на общую нагрузку параллельно с остальными станциями, объединенными в одну эквивалентную ЭС (рис.1). Составим оптимизационную математическую модель. В качестве неизвестных примем | 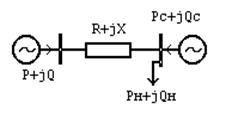 Рис.1
Рис.1
|
активные и реактивные мощности станций, обозначив их, соответственно, векторами P=( P, Pc) и Q=(Q, Qc):
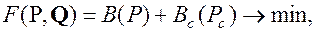
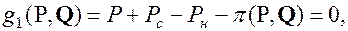 (1)
(1)
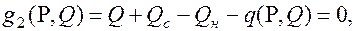
где B(P), Bc(Pc)- расходные характеристики ЭС, тут/ч, Pн, Qн – суммарная нагрузка системы, 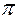 , q – потери активной и реактивной мощности в сети.
, q – потери активной и реактивной мощности в сети.
Нагрузка в сети принимается заданной и независимой от напряжения.
Функция Лагранжа для этой задачи нелинейного программирования имеет вид:
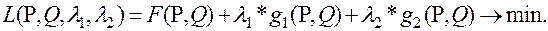 (2)
(2)
Условия минимума функции Лагранжа определяются равенством нулю частных производных по всем неизвестным. Рассмотрим пару таких условий, записанных для рассматриваемой ТЭС:
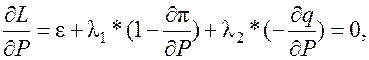
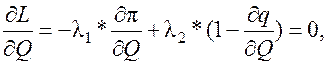 (3)
(3)
где ε –относительный прирост расхода топлива на ТЭС,
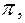 q – потери активной и реактивной мощности в сети.
q – потери активной и реактивной мощности в сети.
Такие пары условий можно записать для каждой ЭС, работающей в системе. Выполнив несложные преобразования получим следующие условия совместного оптимального распределения активной и реактивной мощности
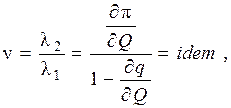
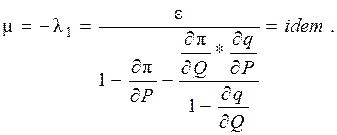 (4)
(4)
Таким образом, параметры μ и ν, определяемые множителями Лагранжа, должны быть одинаковы для всех ТЭС системы.
Оптимизация реактивной мощности вносит некоторые дополнения в условия оптимального распределения активной нагрузки, связанные с более точным учетом потерь в сети.
Объект исследования
В работе исследуется режим работы ТЭС, которая через сеть 110 кВ работает параллельно с системой на общую нагрузку. Расчетная схема исследуемой системы показана на рис 2.
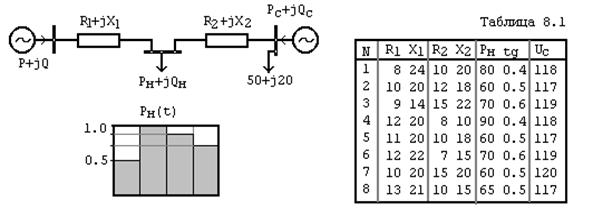
Рис. 2.
Расходные характеристики учитываются многочленами второго порядка
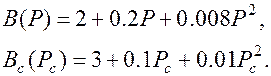
Задан суточный график нагрузки в одном из узлов, мощность нагрузки Рн в часы максимума в МВт, tg(φ) нагрузки, сопротивления Z1 и Z2 ветвей в Ом, напряжение в кВ на шинах системы Uc, принятой за балансирующий узел.
Программное обеспечение
Работа выполняется по программе, записанной в файл под именем ASYLB 8. exe. После активизации программы на экране монитора появляется фронтальная панель лабораторной установки (рис. 3).
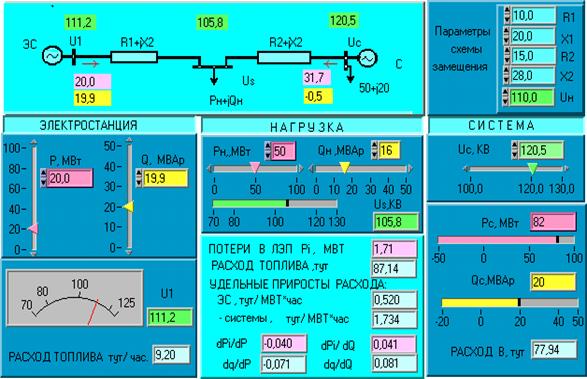
Рис. 3
В верхней части панели изображается расчетная схема исследуемой системы с индикаторами основных параметров режима. Здесь же справа располагаются цифровые задатчики параметров ветвей и номинального напряжения сети.
В нижней части фронтальной панели слева расположены задатчики мощности ТЭС, индикатор напряжения на шинах ее в виде стрелочного прибора и указатель расхода топлива. Справа размещается задатчик напряжения на шинах системы, индикаторы мощности ее и расход топлива.
В центре располагаются задатчики нагрузки и индикатор напряжения в узле. Ниже представлены индикаторы общих потерь в сети, расхода топлива, удельных приростов расхода топлива для станции и системы, а также удельных приростов потерь активной и реактивной мощности в сети.
Порядок выполнения работы
1. В процессе подготовки к работе для заданного варианта определить оптимальное распределение активной мощности без учета потерь и реактивной мощности для режима наибольшей нагрузки. Найти общие потери в сети и общий расход топлива.
2. Активизировать файл ASYLB8. exe и установить с помощью устройств фронтальной панели параметры системы и найденную в п.1 оптимальную мощность станции. Установить нагрузку, соответствующую первой ступени суточного графика. Запустить программу на выполнение и записать следующие параметры режима: t, Pн, Qн, P, Q, U1, Us, Pc, Qc, Uc, B, Bc, Bo, 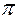 , ε1, εc и все удельные приросты потерь. Аналогично исследовать режим и для остальных ступеней графика. Зная продолжительность ступеней найти суточный расход топлива, выработку энергии на ТЭС и в системе, потери энергии.
, ε1, εc и все удельные приросты потерь. Аналогично исследовать режим и для остальных ступеней графика. Зная продолжительность ступеней найти суточный расход топлива, выработку энергии на ТЭС и в системе, потери энергии.
3. Для каждой ступени графика провести оптимизацию распределения активной мощности без учета потерь по равенству относительных приростов расхода топлива. С этой целью установить заданную нагрузку и в режиме циклического решения меняя Р добиться выполнения условий оптимизации. Заполнить таблицу и оценить эффект от оптимизации. Сравнить полученный результат с расчетом по п.2.
4. Для суточного графика провести оптимизацию Р с учетом потерь. Записать параметры режима. Оценить эффект от учета потерь. При наибольшей нагрузке проверить выполнение условий оптимизации.
5. Для каждой ступени графика выставить найденные ранее оптимальные активные мощности ТЭС и провести оптимизацию Q. Записать параметры в таблицу и оценить эффект от оптимизации.
6. Для заданного графика на каждой ступени провести комплексную оптимизацию. Записать результаты в таблицу и оценить дополнительный эффект от совместной оптимизации. В часы наибольших нагрузок проверить выполнение условий комплексной оптимизации.
7. Для одного из режимов провести оптимизацию с учетом ограничений и оценить потерю экономичности. Ограничения выбрать самостоятельно.
8. Все этапы исследований отразить в отчете.
Контрольные вопросы
1. Какой критерий используется при комплексной оптимизации режима энергосистемы?
2. Как влияет реактивная мощность на расход топлива в системе?
3. Как изменятся условия оптимального распределения, если в качестве балансирующего узла выбирается система?
4. Каким образом на ТЭС регулируется выработка активной и реактивной мощности?
5. Какие ограничения могут учитываться при оптимизации распределения нагрузки в системе?
6. Как влияют ограничения на величину критерия оптимизации?
Лабораторная работа N 8
Дата: 2019-04-23, просмотров: 372.