Б.Г. Булатов
МЕТОДЫ ПРИНЯТИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ
ПРИ РАЗВИТИИ И ЭКСПЛУАТАЦИИ ЭНЕРГОСИСТЕМ
Учебное пособие к лабораторным работам
По направлению
«Электроэнергетика и электротехника
Челябинск
Издательство ЮУрГУ
2016
УДК 621.311
Б907
Одобрено
учебно-методической комиссией энергетического факультета
Рецензенты;
Булатов Б.Г.
Методы принятия оптимальных решений при развитии и эксплуатации энергосистем: Учебное пособие к лабораторным работам.– Челябинск: Издательство ЮУрГУ, 2016. – 48 с.
Приведены описания лабораторных работ, в которых исследуется применение методов линейного и нелинейного программирования для оптимизации принимаемых решений по развитию и управлению режимами объектов энергетических систем, а также средства автоматизации управления. Все работы выполняются на ПЭВМ.
Учебное пособие предназначено для студентов, обучающихся по программам бакалавриата и магистратуры по направлению «Электроэнергетика и электротехника».
ãИздательский центр ЮУрГУ, 2016
ВВЕДЕНИЕ
Предлагаемый лабораторный цикл предназначен для освоения методов использования линейных оптимизационных моделей для решения тех задач, в которых учет нелинейностей практически не влияет на величину критерия оптимизации и при невысокой точности исходных данных не оправдывает возможных сложностей использования нелинейных моделей. Достоинством линейной оптимизации является возможность применения надежного симплекс-метода. К таким задачам относят сегодня задачи развития и принятия решений в тех случаях когда, исходные данные определяются на основе прогнозирования.
Нелинейные модели используются в тех случаях, когда исходная информация более достоверна и учет нелинейностей позволяет увеличить величину экономического критерия. К таким задачам относят выбор оптимальных решений при эксплуатации уже существующих энергетических объектов.
Программное обеспечение разработано в среде проектирования LabVIEW, основанной на языке графического программирования G. Программные модули, созданные в среде LabVIEW, оформлены в виде исполняемых файлов с расширением .exe и могут запускаться только из оболочки Windows. После активизации программного файла в центре экрана дисплея появляется фронтальная панель виртуальгого устройства (ВУ). Выше панели размещаются стандартные для Windows строки. В первой указано имя выполняемой программы. Вторая строка отведена под Меню, которое при выполнении лабораторных работ практически не используется. Ниже располагается панель инструментов, используемая для запуска программы.
При нажатии мышкой первой кнопки этой панели осуществляется одноразовое выполнение программы. Нажатие следующей кнопки с двумя стрелками приводит к циклически повторяющемуся запуску, при котором любое изменение объектов фронтальной панели тут же приводит к адекватному изменению параметров режима и их отображению на индикаторах панели. Выход из циклического режима осуществляется нажатием на кнопку Stop, которая появляется при запуске в строке инструментов.
Отказ от использования физических моделей или реальных установок при изучении специальных дисциплин многократно снижает затраты на создание лабораторного практикума, экономит площади и делает его доступным для индивидуальной самостоятельной работы студентов дневной и заочной формы обучения.
Использование математических моделей изучаемых объектов при современных технических характеристиках ЭВМ создает иллюзию непосредственного взаимодействия с исследуемой системой, что дает возможность в большинстве случаев проводить эксперименты, которые в условиях действующих установок или физических моделей были бы невозможны. Предлагаемые работы позволяют освоить основные понятия и приемы составления математических моделей, описывающих свойства, внутренние и внешние связи рассматриваемых объектов планирования и эксплуатации, закрепить представления о математических методах оптимизации, о приемах оптимизации режимов энергосистем. Одна из работ позволяет сформировать представление о структуре, технических средствах и функционировании автоматизированной системы диспетчерского управления. режимом энергосистемы.
Лабораторная работа №1
Пример оценки инвестиционных критериев проекта малой генерации
В условиях рыночной экономики для оценки инвестиционной привлекательности проекта рассмотрим следующие критерии: чистая текущая стоимость (NPV) или ЧДД; индекс рентабельности ( PI); внутренняя норма доходности ( IRR) и дисконтированный срок окупаемости инвестиции ( DPP).
Наиболее близким к критерию плановой экономики является чистый дисконтированный доход (ЧДД):
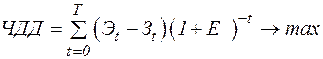 , (3)
, (3)
где 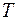 – расчетный срок;
– расчетный срок;
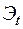 – эффект или поступления;
– эффект или поступления;
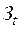 – затраты;
– затраты;
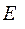 – норма дисканта, определяемая процентом роста банковского капитала.
– норма дисканта, определяемая процентом роста банковского капитала.
При выборе варианта может использоваться понятие срока окупаемости, при котором вложенные средства полностью возвращаются за счет дохода от эксплуатации объекта.
Оценкой эффективности вложений может служить внутренняя норма доходности R, т.е. такое значение нормы дисконтирования, при котором величина разности поступлений и затрат, обозначаемой NPV, равна нулю:
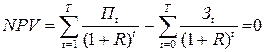 . (4)
. (4)
Условие R > E является оценкой эффективности бизнес-плана.
Индекс прибыльности, который обозначается как PI и определяется следующим образом
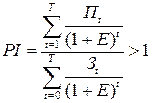 , (5)
, (5)
также определяет целесообразность реализации рассматриваемого варианта.
Для иллюстрации этих экономических понятий проведем упрощенную оценку эффективности затрат на ввод установки малой генерации мощностью 1000 кВт на предприятии с плотным графиком нагрузки (Тм=7000 ч.) для покрытия потребностей в электроэнергии вместо покупки на розничном рынке.
Ориентировочные значения технико-экономических показателей: удельная стоимость оборудования Ко=35тыс.руб/кВт, удельный расход газа Во=0,3 куб.м/кВт.ч, ежегодные расходы на эксплуатацию и ремонт Иэ=4,3 млн. руб., рыночные тарифы на электроэнергию 2,92 руб./кВт.ч и на газ Тг=1,5 руб./куб.м .При этом экономия на стоимости замещаемой годовой энергии составит Э=1000*7000*2,92 =20,45 млн.руб. Ежегодные затраты на газ составят Зг =1,5*0,3*1000*7000=3,15 млн.руб. Общая годовая прибыль составит П=Э-Иэ-Зг=20.45-4.3-3.15=15,0 млн.руб.
Ниже представлена оценка эффективности по рыночным критериям с учетом дисконтирования. При этом несколько усложним задачу, учитывая как разовые с распределением по годам затраты на разработку проекта в объеме 6000 тыс. руб., так и затраты на реализацию проекта, включающие затраты на установку - 35000 тыс.руб. и последующие затраты на утилизацию тепла объемом 10000 тыс. руб. с ожидаемой прибылью в 5000 тыс.руб.
Таким образом, общие инвестиционные расходы:
в течении условного года выполнения проекта: 6000 тыс. руб,.
в течении 1-го года реализации: 35000 тыс. руб.
в течении 2-го года: 10000 тыс. руб.
Прибыль в объеме 15000 тыс.руб. определяется за счет компенсации затрат на покупку электроэнергии за вычетом затрат на газ, ремонт и эксплуатацию, а также за счет эффекта в 5000 тыс.руб. при утилизации тепла и составляет:
во 2-ой год: 15000 тыс. руб.;
в 3-ий и последующие годы: 20000 тыс. руб.;
Без анализа динамики инфляционных процессов ставку дисконта принимаем по проценту роста банковского капитала равного 10%. Расчетный период принят равным Т=7 лет.
Все расчеты сведены в таблицу, в которой финансовые потоки приведены в тыс.рублей.
Таблица 1
| Годы | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Затраты, тыс. руб. | -6000 | -35000 | -10000 | 0 | 0 | 0 | 0 | 0 |
| Поступления, тыс. руб. | 0 | 0 | 15000 | 20000 | 20000 | 20000 | 20000 | 20000 |
| Сальдо | -6000 | -35000 | 5000 | 20000 | 20000 | 20000 | 20000 | 20000 |
| Накопленное сальдо | -6000 | -41000 | -36000 | -16000 | 4000 | 24000 | 44000 | 64000 |
| Норма дисконта | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 |
| Ставка дисконта | 1,0 | 1,1 | 1,21 | 1,33 | 1,46 | 1,61 | 1.77 | 1,95 |
| Дисконтированное сальдо | -6000 | -31820 | 4130 | 15038 | 13670 | 12468 | 11298 | 10271 |
| Накопленное дисконтированное сальдо | -6000 | -37820 | -33690 | -18652 | -4982 | 7486 | 18784 | 29055 |
В расчетах далее объемы затрат представлены в млн. руб.
Чистый дисконтированный доход ЧДД составляет 29,055 млн. руб.
Простой срок окупаемости
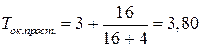 года.
года.
Дисконтированный срок окупаемости
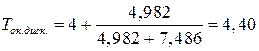 года.
года.
Внутренняя норма доходности R определяется решением нелинейного уравнения, полученного по условию NPV=0:
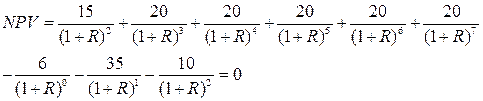
Решение данного уравнения даёт следующее значение внутренней нормы доходности R= 0,4115. Выполнение условия R > E подтверждает высокую эффективность проекта..
Индекс прибыльности определяется следующим образом:
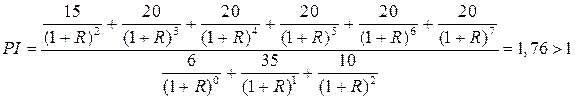
Все рассмотренные критерии сегодня находят применение в практике принятия решений по оптимальному развитию энергосистем и их объектов, в том числе и методы приведенных затрат, которые хотя разрабатывались и применялись в период опережающего развития энергетики и создания ЕЭС СССР, но являются полезными и для текущего этапа развития энергетики России. Конечно, они корректируются с учетом рыночных особенностей, новой структуры и появления компаний с приоритетной направленностью на прибыль.
Порядок выполнения работы
1. Для заданного варианта параметров планируемой мини-ТЭЦ принять расчетный срок 10 лет и норму дисканта Е=15% определить значения финансовых потоков по годам. Объем утилизации тепла Qу принять равным 0,5 от Рм при Тмт=3500 ч. Затраты на проектирование принять ПРэ=6 млн.руб., ПРт=5млн.руб., плату за присоединение принять Прэ=0.
2. По программе Табл.ЧДД. exe определить критерии эффективности плана и сделать выводы о целесообразности его реализации. Определить границы целесообразности в зависимости от роста тарифов и удельной стоимости энергоустановки.
3. По программе AnalisNPV . exe определить критерии эффективности и исследовать устойчивость оценок срока окупаемости при изменении тарифов.
4. Самостоятельно выбрать направление исследования на устойчивость и выполнить анализ.
5. Результаты исследований отразить в отчете.
Таблица 2
| № | Рм, кВт | Тмэ, час | Ко, т.руб/кВт | Во, м3/кВт.ч | Иэ, млн.руб | Тэ, руб/кВт.ч | Тт, руб/Гкал | Тгаз, руб/м3 |
| 1 | 1000 | 6000 | 40 | 0,44 | 6,6 | 2,6 | 800 | 3,0 |
| 2 | 1200 | 5500 | 45 | 0,38 | 7,0 | 2,8 | 750 | 3,5 |
| 3 | 1260 | 5800 | 35 | 0,30 | 7,2 | 2,5 | 680 | 4,0 |
| 4 | 1500 | 5400 | 38 | 0,42 | 7,5 | 3,0 | 700 | 3,7 |
| 5 | 2000 | 5200 | 42 | 0,46 | 8,0 | 3,2 | 810 | 3,0 |
| 6 | 2400 | 4500 | 48 | 0,39 | 8,5 | 2,4 | 760 | 3,5 |
| 7 | 1700 | 5300 | 50 | 0,34 | 7,8 | 2,6 | 670 | 4,0 |
| 8 | 1800 | 5100 | 52 | 0,42 | 7,9 | 2,9 | 720 | 3,7 |
5. Контрольные вопросы
1. Приведенные затраты - критерий плановой экономики.
2. Понятие срока окупаемости.
3. Определение срока окупаемости при разовых вложениях.
4. Срок окупаемости при учете дисконтирования.
5. Смысл и определение ЧДД.
6. Определение внутренней нормы доходности.
7 Понятие индекса прибыльности.
Лабораторная работа №2
Порядок выполнения работы
1. Составить расчетную схему и линейную модель.
2. Решить модель симплекс методом, распределительным методом и методом потенциалов.
3. Определить структуру системы, приняв в составе ЭС блоки 100 и 200 МВт. Выбрать блочные трансформаторы, номинальное напряжение ЛЭП, число цепей и сечение проводов.
4. Привести вариант структурной схемы системы по результатам решения модели.
4. Контрольные вопросы
1. Что входит в состав оптимизационной модели?
2. Идея симплекс метода. Базисные и свободные переменные.
3. Допустимое базисное решение.
4. Открытая и закрытая транспортная задача.
5. Цепочка и ее характеристика
6. Методы составления опорного плана.
Лабораторная работа №3
Линейная модель выбора оптимального плана топливоснабжения
Цель работы: исследование оптимизационной модели топливоснабжения технологического процесса производства тепловой энергии.
Порядок выполнения работы
1. Составить расчетную схему, выбрать переменные и составить математическую модель.
2. Активизировать программу Simple . exe , ознакомиться с возможностями программы, найти решение и показать схему оптимального плана.
3. Определить топливную и транспортную составляющие в себестоимости Гкал, произведенной котельными и отпущенными в тепловые сети.
4. Найти наилучший план при ограничении максимального грузопотока на 40 % из-за возможного повреждения транспортной магистрали.
3. Контрольные вопросы
1. Алгоритм симплекс-метода.
2. Геометрический смысл метода.
3. Алгебра симплекс-метода.
4. Свободные и базисные переменные.
5. Ограничения и фиктивные переменные.
Лабораторная работа №4
ЛИНЕЙНАЯ МОДЕЛЬ ВЫБОРА ПЛАНА РАЗВИТИЯ ЭНЕРГОСИСТЕМЫ
Цель работы: исследование статической линейной модели развития энергосистемы.
Порядок выполнения работы
1. Определить дефицит мощности в системе с ориентировочным учетом потерь, расходов на с.н. и резерва.
2. Составить расчетную схему и определить состав переменных модели (рис.4).
3. Составить линейную оптимизационную модель выбора структуры генерирующих мощностей и новых ЛЭП системы, приняв Со=6,0 руб./(МВт*км) для существующих и Со=10 руб./(МВт*км) для новых ЛЭП.
4. В ограничениях модели учесть условия покрытия дефицита мощности, балансы мощности в узлах, ограничение по годовым объемам выделяемого топлива для каждой базы.
Ограничения модели, реализованные в решении, показанном на рис. 5, учитывают следующие свойства системы:
1- ограничение по предельной мощности КЭС,
2- условие покрытия дефицита мощности,
3,4- ограничения по топливу с баз У1 и У2,
5, 6, 7 – условия баланса мощности в узлах Р1, Р2 и Р3;
8- условие выдачи мощности в систему;
9, 10 – условия баланса на шинах ЭС-1 и ЭС-2;
11- условие баланса на шинах КЭС с четом расходов на с.н.;
12,13 –условия определения годовых расходов топлива с баз У1 иУ2.
В целевой функции учесть затраты на КЭС, в ЛЭП и на топливо с учетом его транспорта.
5. Активизировать программу Simple . exe и решить модель на ЭВМ симплекс-методом. Оценить влияние объемов выделяемого дефицитного топлива на решение.
6. По результатам решения выбрать схему развития системы и основное оборудование ( блоки, блочные трансформаторы и ЛЭП).
На рисунке 4 приведена расчетная схема системы, на которой отмечены выбранные переменные модели. Первые 4 определяют возможные установленные мощности в блоках разного типа при работе на топливе в объеме Х5 и Х6 с разных баз. Остальные переменные определяют возможные потоки по ЛЭП. На рисунке 5 показан вид экранной страницы с решением модели для расчетной схемы, приведенным на рис.4, где показаны и результаты расчета.
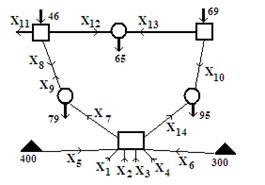
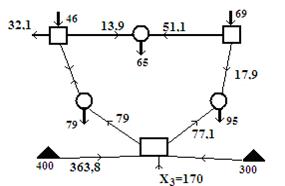
Рис.4
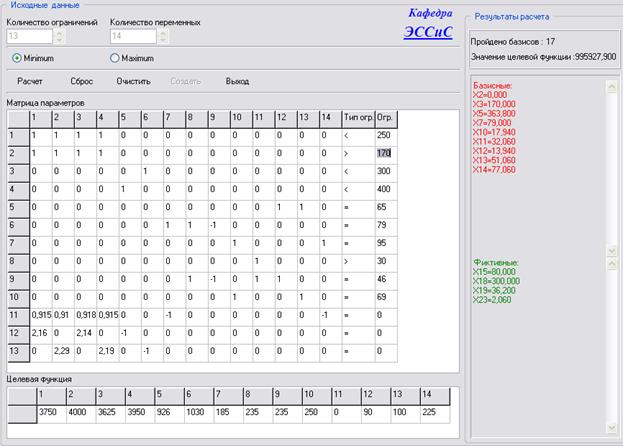
Рис.5
Контрольные вопросы
1. Признаки задач линейного программирования.
2. Геометрический смысл задачи.
3. В чем суть и идея симплекс-метода?
4. Какой смысл имеют фиктивные переменные?
5. Зачем и почему для некоторых линий вводят две переменные?
Лабораторная работа N 5
Математическая модель планирования развития сети
Цель работы: исследование методики составления оптимизационной модели с квадратичной функцией затрат при линейных ограничениях.
Учет затрат в ЛЭП
Затраты в ЛЭП определяются сечением, типом опор и передаваемой мощностью. При планировании заранее не известно сечение ЛЭП, следовательно, затраты в линию необходимо представить функцией только от ее потока мощности, исключив сечение, но сохранив возможность определения сечения по найденному в результате решения модели потоку. Для этой цели может использоваться известный метод экономических интервалов. Рассмотрим суть этого метода.
Затраты на  ЛЭП определенного типа и i-го сечения можно определить как приведенные затраты:
ЛЭП определенного типа и i-го сечения можно определить как приведенные затраты:
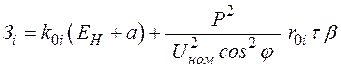 ,
,
где 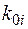 – удельные затраты;
– удельные затраты;
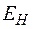 – нормативный коэффициент;
– нормативный коэффициент;
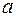 – коэффициент амортизационных отчислений;
– коэффициент амортизационных отчислений;
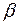 – стоимость потерянной электроэнергии,
– стоимость потерянной электроэнергии,
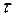 – число часов набольших потерь.
– число часов набольших потерь.
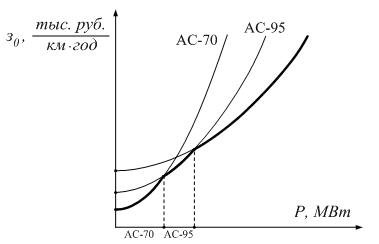
Рисунок 1
Если построить зависимости для всех сечений, допустимых для принятого напряжения 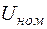 , то получим семейство пересекающихся парабол. На рисунке 1 показаны только 3 сечения ЛЭП 110 кВ.
, то получим семейство пересекающихся парабол. На рисунке 1 показаны только 3 сечения ЛЭП 110 кВ.
По нижней огибающей удельных затрат можно составить выборку и использовать ее для аппроксимации для принятого предиктора методом наименьших квадратов.
3. Применение метода проектирования градиента
Как известно, основное уравнение градиентного метода при безусловной оптимизации:
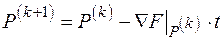 .
.
Здесь P – вектор переменных, F ( P ) – целевая функция, k – номер итерации, t – шаг.
Рассмотрим простейший пример, в котором необходимо выбрать сеть для питания только одного узла (рисунок 2). Полагаем, что затраты представлены квадратичными зависимостями. В качестве исходной точки примем Р0=(0,РН).
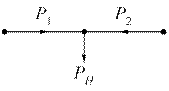
| 
|
Рисунок 2
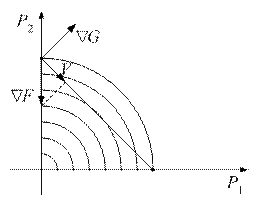
При учете ограничений движение к минимуму должно осуществляться по проекции градиента на поверхность ограничений, т.е. вдоль вектора V . Вектор V можно получить путем исключения из 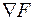 составляющих, перпендикулярных поверхности ограничений. Эти составляющие образуют градиент ограничений
составляющих, перпендикулярных поверхности ограничений. Эти составляющие образуют градиент ограничений 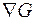 . Таким образом, вектор V определяется по выражению
. Таким образом, вектор V определяется по выражению
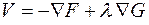 .
.
Для определения неопределенных множителей 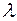 , образующих вектор V, используется условие равенства нулю скалярного произведения:
, образующих вектор V, используется условие равенства нулю скалярного произведения:
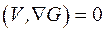 .
.
Из этого условия, приняв для линейного ограничения градиент равным 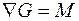 , можно найти
, можно найти 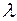 . Действительно, из преобразования
. Действительно, из преобразования
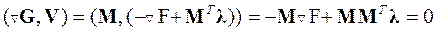
можно получить следующее матричное выражение для множителей 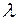
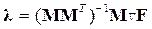 .
.
Составляющие вектора множителей λ позволяют определить все составляющие вектора V
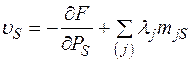 ,
,
и использовать их в процедуре градиентного метода
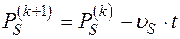 .
.
Определить проекцию градиента V можно, если использовать полученное выше матричное выражение для λ и провести следующее преобразование
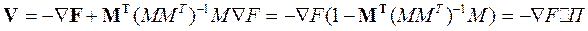 ,
,
где П= 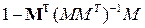 - матрица проектирования.
- матрица проектирования.
Итерационный процесс начинается с выбора исходного приближения и продолжается до тех пор, пока не выполнится условие требуемой точности для всех составляющих 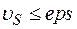 .
.
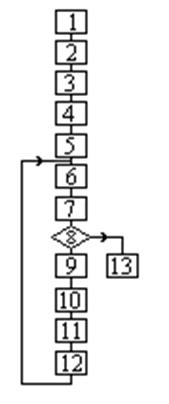
| Блок-схема алгоритма с выбором оптимального шага приведена на рисунке. Назначение блоков:
1. Формирование расчетной схемы.
2. Определение типа функций для расчета затрат и их
производных для всех ветвей.
3. Формирование матрицы инциденций М.
4. Определение матрицы проектирования градиента П.
5. Исходное приближение потоков Р=Р0.
6. Вычисление градиента 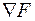 в точке Р.
7. Определение проекции V градиента.
8. Проверка условия окончания в точке Р.
7. Определение проекции V градиента.
8. Проверка условия окончания 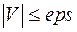 .
9. Организация пробного шага Р1= Р- V t 0/ .
10. Вычисление градиента и проекции V1 в конце шага.
11. Определение оптимального шага .
9. Организация пробного шага Р1= Р- V t 0/ .
10. Вычисление градиента и проекции V1 в конце шага.
11. Определение оптимального шага
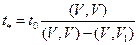 .
12. Рабочий шаг .
12. Рабочий шаг 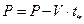 .
13. Вывод результатов .
13. Вывод результатов
|
Объект исследования
В качестве объекта исследования принята проектируемая сеть 110 кВ, расчетная схема которой представлена в виде графа сети на рисунке 3. Нагрузки в узлах, длины возможных ЛЭП приведены в таблице.
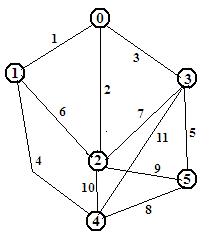
Рисунок 3
Таблица 1
| № | Длины ЛЭП, км | Нагрузки, МВт | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 1 | 2 | 3 | 4 | 5 | |
| 1 | 30 | 40 | 25 | 28 | 30 | 30 | 40 | 25 | 30 | - | - | 35 | 45 | 25 | 15 | 15 |
| 2 | 28 | 35 | 40 | - | 28 | 30 | 30 | 40 | 25 | 30 | - | 42 | 27 | 31 | 18 | 20 |
| 3 | 20 | 45 | 35 | - | - | 28 | 30 | 30 | 40 | 25 | 30 | 28 | 33 | 39 | 22 | 18 |
| 4 | 40 | 35 | 30 | 28 | 30 | 30 | - | 28 | 30 | 35 | - | 30 | 50 | 20 | 15 | 20 |
| 5 | 30 | 40 | 25 | - | 28 | 30 | 30 | - | 28 | 30 | 35 | 35 | 40 | 25 | 18 | 15 |
| 6 | 28 | 35 | 40 | - | 40 | 28 | 30 | 30 | - | 35 | 40 | 42 | 27 | 35 | 18 | 22 |
| 7 | 20 | 45 | 35 | 30 | 35 | - | 30 | 35 | - | 30 | 35 | 28 | 30 | 39 | 25 | 18 |
| 8 | 40 | 35 | 30 | 42 | - | - | 35 | 28 | 30 | 24 | 32 | 30 | 40 | 20 | 15 | 22 |
Исследование проводится с использованием программы, фронтальная панель которой показана на рисунке 4. В верхней части расположены приборы для ввода исходной информации по сети: количества узлов Ny и ветвей Nv, матрицы соединений М, вектора исходного приближения потоков по ветвям Ро, вектора коэффициентов градиента затрат по ветвям сети dF, пробного шага to и точности eps.
Рисунок 4
В нижней половине показаны результаты работы алгоритма оптимизации: матрица проектирования, исходные потоки по ветвям и общие затраты, число итераций и потоки по ветвям в оптимальной схеме. Ниже в массивах выведены для всех итераций текущие значения потоков Po , градиента dF и его проекции V, а также их значения в конце пробного шага, т.е. потока P1, градиента dF1 и проекции V1. Выведены и значения оптимального шага на итерациях
Чтобы посмотреть эти результаты надо на верхнем цифровом индикаторе номера элемента (строки) установить номер итерации, а на нижнем номер ветви, с которой начинается зона вывода. При этом нумерация начинается с нуля.
Для любознательных, знакомых с основами программирования в среде LabVIEW, на рисунке 5 показана программа оптимизации, написанная на языке графического программирования LabVIEW.
Порядок выполнения работы
1. Построить зависимости удельных затрат для ЛЭП 110 кВ. Стоимость 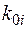 для выбранного типа линий принять по справочнику, нормативный коэффициент Ен=0,15; коэффициент амортизационных отчислений а=0,1; стоимость потерянной электроэнергии в руб/кВт*ч принять
для выбранного типа линий принять по справочнику, нормативный коэффициент Ен=0,15; коэффициент амортизационных отчислений а=0,1; стоимость потерянной электроэнергии в руб/кВт*ч принять 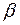 =2+0,1*№, Тм=5000 ч., cos=0,9.
=2+0,1*№, Тм=5000 ч., cos=0,9.
2. Определить экономические интервалы для всех сечений.
3. Составить выборку по нижней огибающей затрат и методом наименьших квадратов найти коэффициенты предиктора З=а+в Р2 .
4. Для заданной схемы сети ввести сплошную нумерацию ветвей, начиная с дерева, выбрать положительные направления ветвей и составить матрицу М. Определить исходное приближение Ро потоков, приняв в качестве его потокораспределение в дереве.
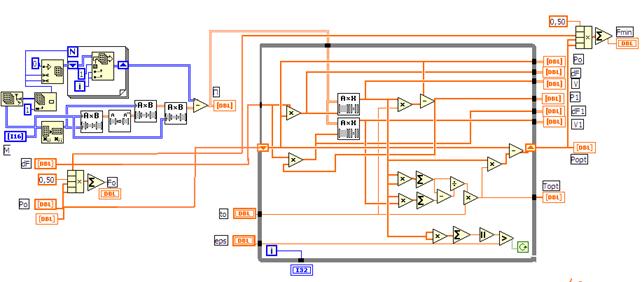 Рисунок 5
Рисунок 5
5. Определить коэффициенты в составляющих градиента для упрощенной целевой функции
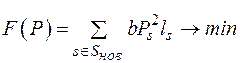 .
.
6. Активизировать программу Gradient . exe или Gradient . vi . Ввести исходные данные.
7. Для одной из ветвей построить графики итерационного процесса, т.е. отобразить изменение потока Po , градиента dF и его проекции V, а также значений в конце пробного шага P1, dF1 и V1.
8. Определить сечение ЛЭП по методу экономических интервалов.
9. Оценить возможности учета коэффициента а предиктора затрат в алгоритме выбора сети.
Контрольные вопросы
1. В чем смысл градиентного метода?
2. Для чего применяется проектирование градиента?
3. Как учитывается конфигурация сети?
4. Дерево и хорды в схеме сети
5. Как определить число деревьев в схеме.
6. Метод экономических интервалов и его применение.
7. Суть метода ветвей и границ для выбора сети.
Лабораторная работа N 6
ПАРАМЕТРЫ РЕЖИМА ЭНЕРГОСИСТЕМЫ
Цель работы: исследование параметров режима энергосистемы и разделение их на независимые и зависимые с оценкой влияния на критериальные функционалы, определяющие экономичность режима.
1. Общие сведения
Режимом энергосистемы называется некоторое состояние ее, определяемое значениями расхода топлива, давления и температуры пара на ТЭС, напора и расхода воды на ГЭС, частоты, напряжения токов, мощностей и других физических величин, называемых параметрами режима, которые характеризуют процесс производства, передачи, преобразования и распределения электрической энергии. Параметры режима делятся на технологические и электрические.
Стационарный режим электрической системы при известных параметрах системы, определяемых составом включенного в работу оборудования и его техническими характеристиками, описывается системой нелинейных алгебраических уравнений, обычно узловых
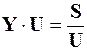 , (1)
, (1)
где Y – матрица узловых проводимостей, U – вектор узловых напряжений,
S – вектор узловых мощностей.
При заданных мощностях Si всех узлов кроме балансирующего и напряжении Uo в этом узле решение системы позволяет найти все остальные узловые напряжения. Для решения могут использоваться различные итеративные и прямые методы. Полученные напряжения позволяют определить любые интересующие параметры режима: потоки и токи ветвей, фазовые углы векторов напряжений, потери в сети, расход топлива на ТЭС и т.п.
Узловые мощности и Uo относятся к независимым параметрам режима, Мощности нагрузочных узлов определяются потребителями электроэнергии и в нормальных ситуациях должны быть обеспечены режимом энергосистемы. Мощности генерирующих узлов могут меняться по заданию диспетчера энергосистемы с целью обеспечения требований надежности, качества и оптимальности режима. В энергосистемах, где электрическая сеть имеет разные номинальные напряжения и автотрансформаторы связи, диспетчер может влиять на режим путем изменения их коэффициентов трансформации К. Диспетчер, наконец, может изменять также и состав включенного в работу оборудования (блоков на электростанциях, ЛЭП и автотрансформаторов).
Таким образом все множество электрических параметров режима можно разделить на следующие группы.
1. Узловые нагрузки Pi, Qi, которые являются заданными.
2. Мощности источников Pj, Qj, напряжение в балансирующем узле Uo, коэффициенты трансформации К, которые подвластны диспетчеру энергосистемы. Их назовем независимыми параметрами режима и объединим в вектор X. В качестве своеобразного независимого параметра можно рассматривать и состав включенного в работу оборудования.
3. Все остальные параметры режима, которые являются зависимыми и образуют вектор Y.
В задаче оптимизации режима составляющие xi вектора X определяются по условию минимума затрат на топливо или, в отдельных подзадачах, минимума потерь в сети. При этом поиск оптимального режима должен проводиться в области допустимых режимов, определяемой условиями надежности и качества.
При исследовании на ЭВМ реализованная имитационная модель режима электрической системы строится на использовании метода Ньютона первого порядка. С этой целью на основе (1) формируется вектор-функция небалансов узловых токов
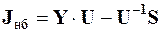 . (2)
. (2)
Действительные и мнимые составляющие тока небаланса для i-го узла будут
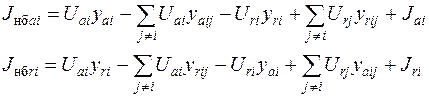 (3)
(3)
По методу Ньютона функция небаланса заменяется разложением в ряд Тейлора в точке с текущим значением U=Uo :
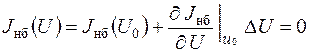 , (4)
, (4)
откуда определяется приращение напряжения
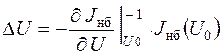
и основное уравнение итерационного процесса
Метод Ньютона имеет хорошую сходимость.
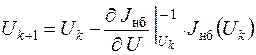 .
.
Объект исследования
Все исследования проводятся для энергосистемы, расчетная схема которой показана на рис.1. В системе 7 независимых узлов, в том числе 4 нагрузочных и 3 генерирующих (2 КЭС и 1 СК), 10 ветвей, в том числе 2 АТ и 2 двухцепных ЛЭП. В качестве балансирующего приняты шины 220 КВ соседней системы. На схеме приведены сопротивления ветвей и величины заданных параметров режима. Для ветвей указаны принятые положительные направления потоков.
Вектор независимых параметров режима ограничен и включает Uo - напряжение в балансирующем узле, P1 и Р2– активную мощность КЭС, Q1, Q2 –реактивную мощность КЭС, K1 - коэффициент трансформации АТ-1, Qск - мощность синхронного компенсатора. Предусмотрена возможность изменения состава оборудования.
3. Программное обеспечение
Лабораторная работа проводится с использованием программы ACYLB1.exe.
После вызова программы проводится расчет режима исследуемой системы при исходных значениях независимых параметров режима, которые устанавливаются на виртуальных потенциометрах независимых параметров режима. Расход топлива и потери в сети отображаются снизу в левой части экрана.
Рекомендуемые ограничения независимых параметров режима:
40  Р
Р  90, 10
90, 10 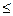 Q
Q 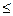 50, 0
50, 0 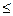 Qск
Qск 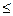 50, 210
50, 210 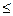 Uo
Uo 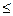 230, 0.45
230, 0.45 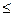 K1
K1 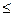 0.55.
0.55.
Порядок выполнения работы
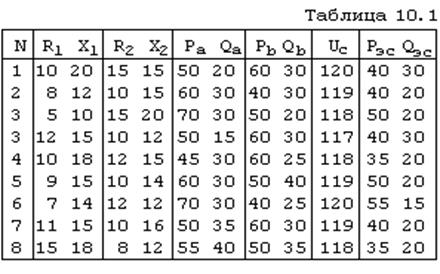
1. Запустить программу и выставить расчетный режим в соответствии с вариантом (таблица 1). Для этого поочередно выставлять заданные значения независимых параметров в любой последовательности. Все дальнейшие исследования проводятся для установленного режима.
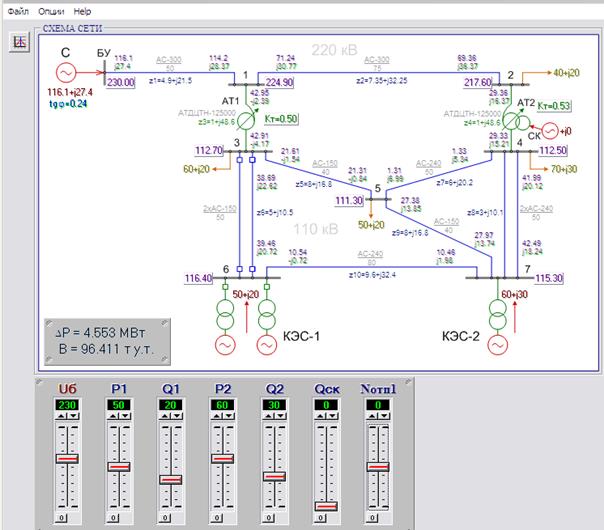
Рис 1. Схема исследуемой энергосистемы
Таблица 1.
| № | Р1 | Q1 | К | P2 | Q2 | Uo |
| 1 | 0 | 20 | 0,50 | 50 | 40 | 215 |
| 2 | 10 | 30 | 0,52 | 45 | 30 | 220 |
| 3 | 20 | 40 | 0,54 | 30 | 20 | 223 |
| 4 | 30 | 50 | 0,48 | 35 | 20 | 228 |
| 5 | 40 | 60 | 0,46 | 20 | 30 | 218 |
| 6 | 50 | 70 | 0,50 | 25 | 20 | 216 |
| 7 | 15 | 40 | 0,52 | 30 | 25 | 218 |
| 8 | 25 | 30 | 0,53 | 40 | 35 | 215 |
2. Построить зависимости потерь dP, расхода топлива B, напряжения в узле i и потока P+ jQ в ветви s от независимых параметров режима, определенных преподавателем.
3. Оценить влияние состава работающего оборудования на режим системы.
4. Определить производные потерь, называемые удельными приростами, в расчетном режиме по независимым параметрам методом конечных приращений.
5. Определить удельный прирост расхода топлива методом конечных и центрированных приращений. Оценить погрешность метода.
6. Определить оптимальное значение К1 без учета и с учетом заданных ограничений. Построить зависимость уравнительного потока от К.
7. Методом покоординатной оптимизации провести комплексную оптимизацию режима и оценить эффект.
8. Все результаты исследований представить в отчете.
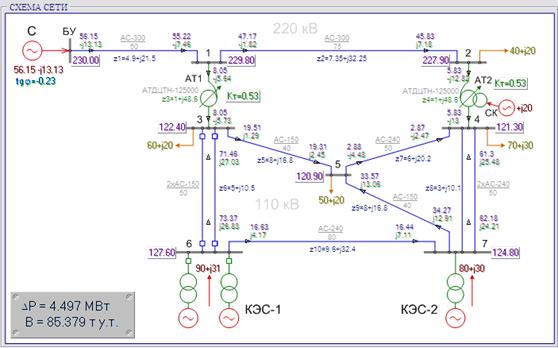
Рис. 2. Исходный режим энергосистемы
Контрольные вопросы
1. Какие параметры режима относятся к независимым ?
2. Что входит в вектор зависимых параметров режима?
3. Критерии оптимизации для поиска оптимальных значений различных параметров режима.
4. Назовите некоторые ограничения, которые необходимо учитывать при оптимизации.
5. Как учитывается конфигурация сети в узловом уравнении ?
6. Как влияет изменение коэффициента трансформации АТ на расход топлива в системе?
7. Как влияет изменение состава включенного оборудования на режим энергосистемы?
Лабораторная работа N 7
КОМПЛЕКСНАЯ ОПТИМИЗАЦИЯ РЕЖИМА ТЭС В СИСТЕМЕ
Цель работы : Исследование критериев и методов комплексной оптимизации режима теплоэнергетической системы и оценка эффекта от оптимального распределения активной и реактивной нагрузки.
Общие сведения
Задача комплексной оптимизации режима энергосистемы заключается в поиске такого распределения активных и реактивных мощностей между источниками при котором обеспечивается минимальный расход топлива на тепловых станциях для каждой ступени суточного графика.
| Рассмотрим энергосистему, в которой можно выделить одну ТЭС, работающую через сеть на общую нагрузку параллельно с остальными станциями, объединенными в одну эквивалентную ЭС (рис.1). Составим оптимизационную математическую модель. В качестве неизвестных примем | 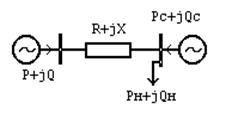 Рис.1
Рис.1
|
активные и реактивные мощности станций, обозначив их, соответственно, векторами P=( P, Pc) и Q=(Q, Qc):
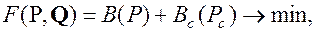
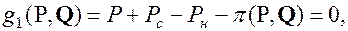 (1)
(1)
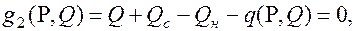
где B(P), Bc(Pc)- расходные характеристики ЭС, тут/ч, Pн, Qн – суммарная нагрузка системы, 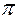 , q – потери активной и реактивной мощности в сети.
, q – потери активной и реактивной мощности в сети.
Нагрузка в сети принимается заданной и независимой от напряжения.
Функция Лагранжа для этой задачи нелинейного программирования имеет вид:
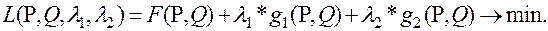 (2)
(2)
Условия минимума функции Лагранжа определяются равенством нулю частных производных по всем неизвестным. Рассмотрим пару таких условий, записанных для рассматриваемой ТЭС:
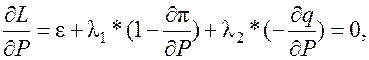
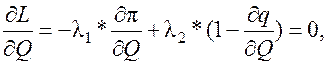 (3)
(3)
где ε –относительный прирост расхода топлива на ТЭС,
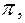 q – потери активной и реактивной мощности в сети.
q – потери активной и реактивной мощности в сети.
Такие пары условий можно записать для каждой ЭС, работающей в системе. Выполнив несложные преобразования получим следующие условия совместного оптимального распределения активной и реактивной мощности
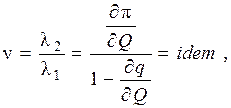
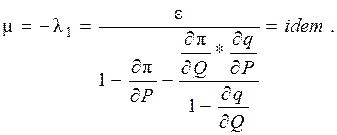 (4)
(4)
Таким образом, параметры μ и ν, определяемые множителями Лагранжа, должны быть одинаковы для всех ТЭС системы.
Оптимизация реактивной мощности вносит некоторые дополнения в условия оптимального распределения активной нагрузки, связанные с более точным учетом потерь в сети.
Объект исследования
В работе исследуется режим работы ТЭС, которая через сеть 110 кВ работает параллельно с системой на общую нагрузку. Расчетная схема исследуемой системы показана на рис 2.
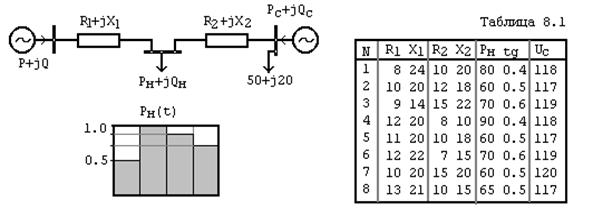
Рис. 2.
Расходные характеристики учитываются многочленами второго порядка
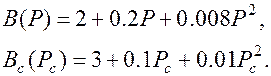
Задан суточный график нагрузки в одном из узлов, мощность нагрузки Рн в часы максимума в МВт, tg(φ) нагрузки, сопротивления Z1 и Z2 ветвей в Ом, напряжение в кВ на шинах системы Uc, принятой за балансирующий узел.
Программное обеспечение
Работа выполняется по программе, записанной в файл под именем ASYLB 8. exe. После активизации программы на экране монитора появляется фронтальная панель лабораторной установки (рис. 3).
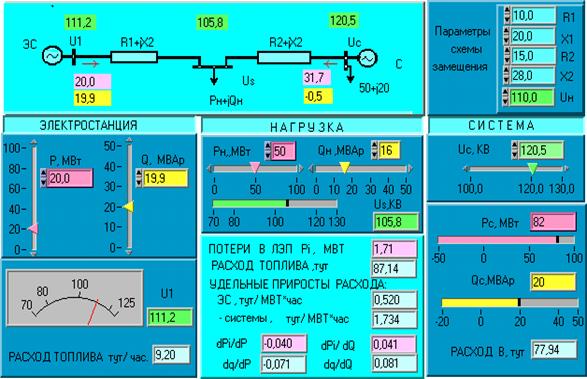
Рис. 3
В верхней части панели изображается расчетная схема исследуемой системы с индикаторами основных параметров режима. Здесь же справа располагаются цифровые задатчики параметров ветвей и номинального напряжения сети.
В нижней части фронтальной панели слева расположены задатчики мощности ТЭС, индикатор напряжения на шинах ее в виде стрелочного прибора и указатель расхода топлива. Справа размещается задатчик напряжения на шинах системы, индикаторы мощности ее и расход топлива.
В центре располагаются задатчики нагрузки и индикатор напряжения в узле. Ниже представлены индикаторы общих потерь в сети, расхода топлива, удельных приростов расхода топлива для станции и системы, а также удельных приростов потерь активной и реактивной мощности в сети.
Порядок выполнения работы
1. В процессе подготовки к работе для заданного варианта определить оптимальное распределение активной мощности без учета потерь и реактивной мощности для режима наибольшей нагрузки. Найти общие потери в сети и общий расход топлива.
2. Активизировать файл ASYLB8. exe и установить с помощью устройств фронтальной панели параметры системы и найденную в п.1 оптимальную мощность станции. Установить нагрузку, соответствующую первой ступени суточного графика. Запустить программу на выполнение и записать следующие параметры режима: t, Pн, Qн, P, Q, U1, Us, Pc, Qc, Uc, B, Bc, Bo, 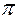 , ε1, εc и все удельные приросты потерь. Аналогично исследовать режим и для остальных ступеней графика. Зная продолжительность ступеней найти суточный расход топлива, выработку энергии на ТЭС и в системе, потери энергии.
, ε1, εc и все удельные приросты потерь. Аналогично исследовать режим и для остальных ступеней графика. Зная продолжительность ступеней найти суточный расход топлива, выработку энергии на ТЭС и в системе, потери энергии.
3. Для каждой ступени графика провести оптимизацию распределения активной мощности без учета потерь по равенству относительных приростов расхода топлива. С этой целью установить заданную нагрузку и в режиме циклического решения меняя Р добиться выполнения условий оптимизации. Заполнить таблицу и оценить эффект от оптимизации. Сравнить полученный результат с расчетом по п.2.
4. Для суточного графика провести оптимизацию Р с учетом потерь. Записать параметры режима. Оценить эффект от учета потерь. При наибольшей нагрузке проверить выполнение условий оптимизации.
5. Для каждой ступени графика выставить найденные ранее оптимальные активные мощности ТЭС и провести оптимизацию Q. Записать параметры в таблицу и оценить эффект от оптимизации.
6. Для заданного графика на каждой ступени провести комплексную оптимизацию. Записать результаты в таблицу и оценить дополнительный эффект от совместной оптимизации. В часы наибольших нагрузок проверить выполнение условий комплексной оптимизации.
7. Для одного из режимов провести оптимизацию с учетом ограничений и оценить потерю экономичности. Ограничения выбрать самостоятельно.
8. Все этапы исследований отразить в отчете.
Контрольные вопросы
1. Какой критерий используется при комплексной оптимизации режима энергосистемы?
2. Как влияет реактивная мощность на расход топлива в системе?
3. Как изменятся условия оптимального распределения, если в качестве балансирующего узла выбирается система?
4. Каким образом на ТЭС регулируется выработка активной и реактивной мощности?
5. Какие ограничения могут учитываться при оптимизации распределения нагрузки в системе?
6. Как влияют ограничения на величину критерия оптимизации?
Лабораторная работа N 8
БЛОКАМИ КЭС
Общие сведения
Задача оптимального распределения мощности между блоками КЭС заключается в поиске минимума расхода топлива
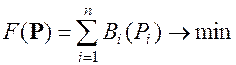
с учетом ограничений по балансу мощности
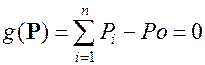 .
.
Здесь Р– вектор активных мощностей блоков, n– число включенных в работу блоков КЭС, B i ( Pi)– расходная характеристика в тут/ч, Po – суммарная мощность КЭС.
Как известно, условием оптимального распределения нагрузки является равенство удельных приростов расхода топлива для всех параллельно работающих блоков
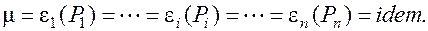
При нарушении этого условия, например для двух блоков из общего числа работающих (рис 1), фактическая нагрузка которых P1 и Р2 отличается от оптимальной Р1о и Р2о, а относительные приросты различны, причем 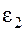 < μ , a
< μ , a 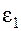 >μ. Очевидно при сохранении баланса на КЭС перегрузка первого блока ΔР1 будет равна недогрузке второго ΔР2. Расход топлива на 1-м блоке будет больше оптимального на величину
>μ. Очевидно при сохранении баланса на КЭС перегрузка первого блока ΔР1 будет равна недогрузке второго ΔР2. Расход топлива на 1-м блоке будет больше оптимального на величину
Р1
Δ В1= ∫ ε1(Р1) dР1 ,
Р1о
пропорциональную площади S1. На втором блоке снижение расхода топлива будет пропорционально площади S2. Перерасход топлива на этих блоках будет пропорционален площади фигуры a-b-c-d.
Общий перерасход топлива на КЭС, называемый пережогом, можно определить суммированием отклонений Δ В i по всем блокам.
На этой основе можно составит алгоритм контроля загрузки блоков и определения пережога топлива при отклонении нагрузки от оптимальной. Данные о фактической нагрузке каждого блока должны вводиться путем циклического опроса датчиков, в качестве которых могут использоваться измерительные преобразователи типа Е с унифицированным выходным сигналом 0-5 мА. Необходимая информация по характеристикам блоков εi ( Pi) вводится по точкам в виде таблицы. Блок-схема алгоритма показана на рис. 2.
Рис. 1 Рис. 2
Функции, выполняемые блоками алгоритма:
1. Ввод характеристик блоков εi(Pi).
2. Опрос датчиков Pi.
3. Определение суммарной нагрузки КЭС Ро.
4. Исходное приближение относительного прироста μ=μо.
5. Зануление Рс=0.
6. Цикл по блокам.
7. Определение Piо методом линейной интерполяции по характеристике εi(Pi) при εi=μ.
8. Рс=Рс+Pio,
9. Определение небаланса dP= Pc- Po.
10. Проверка условия abs( dP)< eps.
11. Корректировка μ.
12. Расчет отклонений расхода топлива по каждому блоку.
13. Определение пережога топлива по КЭС.
14. Отображение результатов на экране.
Выводимые на панель устройства фактические и оптимальные мощности блоков, отклонения расходов топлива и общий пережог помогают ДИСу принять обоснованные решения по перераспределению нагрузки между блоками. Рассмотренный алгоритм можно реализовать с помощью микропроцессора или ПЭВМ.
Объект исследования
В работе исследуется устройство, выполненное на ПЭВМ в среде графического программирования LabVIEW, и предназначенное для контроля работы КЭС, на которой установлены 4 блока ТГВ-300.
Предполагается, что характеристики удельных расходов и относительных приростов блоков известны.
Программное обеспечение
Работа выполняется по программам, записанным в файл под именами ASYLB9 c. exe или ASYLB9. exe. Первая программа устанавливается только на тех ПЭВМ, которые имеют плату сопряжения LabPC+, позволяющую подключить к устройству измерительные преобразователи мощности блоков. В работе преобразователи имитируются потенциометрами, выходные напряжения которых, пропорциональные мощности блоков, регулируются вручную и через специальное устройство, называемое коннектором, вводятся в ПЭВМ.
Файл с именем ASYLB9. exe не требует платы сопряжения. Входные мощности здесь имитируются цифровыми задатчиками, расположенными на фронтальной панели виртуального устройства (рис. 3) возле каждого блока мнемонической схемы КЭС. Блоки на этой схеме подключаются к шинам с помощью управляемых виртуальных выключателей, что позволяет достаточно просто менять состав работающих блоков.
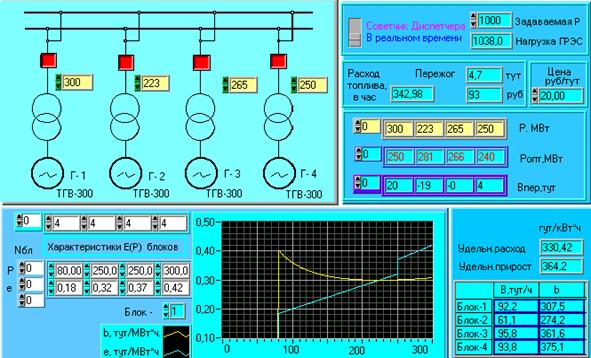
Рис. 3
Ниже схемы КЭС на панели расположены массивы для ввода характеристик относительных приростов εi(Pi). Элементы массивов нумеруются, начиная с нуля. Для каждого блока в соответствующем массиве задается количество точек вводимой характеристики.
Ввод или просмотр характеристик εi(Pi) и bi(Pi) проводится при отключенном положении всех блочных выключателей. Номер просматриваемой характеристики указывается на соответствующем задатчике.
Справа в верхней части панели располагается переключатель выбора режима работы устройства. Режим “Советчик диспетчера” используется для оптимального распределения планируемой нагрузки КЭС между блоками, состав которых определяется включением виртуальных выключателей, а нагрузка КЭС задается с помощью цифрового задатчика.
Ниже располагается задатчик цены топлива и индикаторы пережога. Здесь же выводится часовой расход топлива по КЭС.
В середине правой части панели выводятся массивы фактических мощностей, оптимальных и отклонений расхода топлива по каждому блоку. Ниже в таблице для каждого блока приведена нагрузка, удельный расход и относительный прирост в тут/МВт*ч.
Порядок выполнения работы
1. Активизировать программу. В режиме советчика в отключенном положении всех блоков просмотреть все характеристики на дисплее. Для этого надо установить номер блока и нажать кнопку одноразового запуска программы.
2. Включить все выключатели и выставить произвольные нагрузки блоков на цифровых задатчиках. Установить режим реального времени. Запустить программу и записать результаты распределения.
3. Изменяя нагрузку блоков при сохранении общей мощности КЭС оценить влияние отклонений мощности от оптимальной на пережог топлива.
4. В соответствии с результатами оценки экономичности перераспределить нагрузку между блоками, сохранив общую нагрузку КЭС, и убедиться в получении эффекта. Оценить экономию топлива за расчетный период (сутки, год).
5. В режиме советчика диспетчера определить оптимальную загрузку блоков при различной общей нагрузке КЭС внутри рабочего диапазона. Записать и оценить результаты оптимизации.
6. В этом же режиме при заданной нагрузке и времени простоя (таблица 8) найти оптимальный состав включенных в работу блоков методом направленного перебора, анализируя соотношения удельных расходов и относительных приростов расхода блоков.
Таблица 8
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Р, МВт | 450 | 460 | 470 | 480 | 490 | 500 | 510 | 520 |
| T пр. | 2 | 3 | 4 | 2 | 3 | 4 | 5 | 6 |
Провести выбор без учета и с учетом пусковых расходов, приняв для времени простоя tпр < 5 час линейную зависимость Впуск=10*tпр (тут).
7. Все этапы исследований отразить в отчете.
Контрольные вопросы
1. Что является критерием для оптимального распределения активной мощности между блоками КЭС?
2. Как изменить активную и реактивную нагрузку блока?
3. Какой физический смысл имеет относительный прирост?
4. Условие оптимального распределения нагрузки между блоками и его физический смысл.
5. По какому критерию выбирается оптимальный состав блоков?
6. Чем определяются пусковые расходы блоков?
7. Как зависят пусковые расходы от времени простоя блока?
Лабораторная работа N 9
Программное обеспечение
Исследование проводится с помощью программы ASYLB10. exe.
После активизации файла на экране изображается фронтальная панель виртуального устройства (рис. 3). В левой части панели расположена схема энергосистемы с виртуальными выключателями на ЛЭП-1 и индикаторами реальных параметров режима. Здесь же показаны все три КП и линии связи с ПУ «Гранит». Возле линий размещены индикаторы содержимого информационных байтов ТС и ТИ. Для системы ТИ результаты измерений представлены целым числом квантов. Для КП1 они выведены в двоичном и десятичном виде.
Ниже схемы располагаются цифровые задатчики параметров ЛЭП и нагрузок в узлах. Здесь же расположены индикаторы потерь мощности в сети, переключатель модификации измерительного преобразователя Е-855 и задатчик периода опроса.
В правой части экрана показано размещение некоторого оборудования диспетчерского щита управления энергосистемой. Здесь показана структура КИО-3, мнемонический щит и рабочая станция, на которой отображены результаты телеизмерений, «псевдоизмерения» и оцениваемые нагрузки узлов. Ниже расположены задатчики , определяющие напряжение на шинах системы и мощность, вырабатываемую электростанцией.
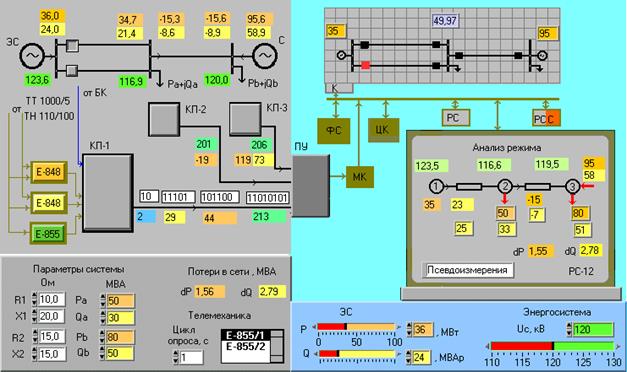
Рис. 3
.4. Порядок выполнения работы
1. В процессе подготовки к работе по заданным параметрам первичных преобразователей определить масштабы квантов в системе ТИ мощности и напряжения. Определить способ определения напряжения в кВ для обеих модификаций преобразователя Е-855.
2. В соответствии с вариантом (табл.1) установить параметры схемы замещения ЛЭП и узловые нагрузки, а также мощность ЭС и напряжение на шинах системы. Запустить программу в режиме одноразового решения. Записать значения параметров режима и проверить содержимое информационных байтов в системе ТС и ТИ.
3. Определить значения “псевдоизмерений“ Q2 в ЛЭП-2 и предложить способ определения их по данным телеметрии. Оценить возможность проверки достоверности измерений P1,Q1,U1 и Us, учитывая некоторую избыточность их. В качестве контроля использовать сравнение “псевдоизмерения“ Q1 с замером
.
4. Сравнить результаты оценки нагрузок в узлах с фактической нагрузкой и предложить упрощенный алгоритм для получения этих оценок с использованием формул для расчета звена передачи.
5. В режиме циклического решения провести откючение одной цепи ЛЭП и объяснить характер изменения параметров режима. Оценить работу сигнальной системы при разных циклах опроса.
6. Оценить влияние на точность представления режима разных модификаций преобразователя Е-855.
7. В режиме циклического решения просмотреть несколько режимов при разных мощностях ЭС и оценить изменение точности отображения режима системы.
8. Все этапы исследований отразить в отчете.
Контрольные вопросы
1. Основные функции АСДУ энергосистемы.
2. Назначение ОИК.
3. Перечислить основные элементы технического обеспечения АСДУ.
4. Назначение средств телемеханики.
5. Как определяется масштаб кванта в системе ТИ?
6. Каковы причины погрешностей в отображении режима энергосистемы?
7. Назначение основных элементов КИО-3?
8. Какие средства связи используются в телемеханике?
9. Какой способ опроса используется в системах ТИ и ТС? 
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Арзамасцев Д.А.. АСУ и оптимизация режимов энергосистем: Учебн. пособие для студентов вузов/ Д.А. Арзамасцев, П.И. Бартоломей, А.М .Холян; Под ред. Д.А. Арзамасцева.–М.: Высш. шк., 1983.–208 с. ил.
2. Электрические системы: Электрические расчеты, программирование и оптимизация режимов/ Под ред. В.А. Веникова.– М.: Высшая школа, 1973.
4. Электрические системы: Автоматизированные системы управления режимами энергосистем/ Под ред. В.А. Веникова.– М.: Высшая школа, 1973.
5. Веников В.А. Оптимизация режимов электростанций и энергосистем: Учебник.– М.: Высш. школа, 1983.
6. Булатов Б.Г. АСУ и оптимизация режимов энергосистем: Учебное пособие к лабораторным работам. – Челябинск: Изд. ЮУрГУ, 2000.
7. Булатов Б.Г. Оптимизация режимов систем генерации: учебное пособие/
Б.Г. Булатов. – Челябинск: Издательский центр ЮУрГУ, 2013.
ОГЛАВЛЕНИЕ
| ВВЕДЕНИЕ , . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 3 | |
| 1. | ИССЛЕДОВАНИЕ КритериЕВ оценки эффективности инвестиционных проектов развития. . . . . . . . . . . . . . . . . | 5 |
| 2 | Исследование линейных оптимизационных моделей. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 14 |
| 3 | Линейная модель выбора оптимального плана топливоснабжения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 16 |
| 4 | ЛИНЕЙНАЯ МОДЕЛЬ ВЫБОРА ПЛАНА РАЗВИТИЯ ЭНЕРГОСИСТЕМЫ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 19 |
| 5 | МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПЛАНИРОВАНИЯ РАЗВИТИЯ СЕТИ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 22 |
| 6 | ПАРАМЕТРЫ РЕЖИМА ЭНЕРГОСИСТЕМЫ. . . . . . . . . . . . . . . . | 29 |
| 7 | КОМПЛЕКСНАЯ ОПТИМИЗАЦИЯ РЕЖИМА ТЭС В СИСТЕМЕ | 32 |
| 8 | О ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ БЛОКАМИ КЭС. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 38 |
| 9 | АВТОМАТИЗИРОВАННАЯ СИСТЕМА ДИСПЕТЧЕРСКОГО УПРАВЛЕНИЯ РЕЖИМОМ ЭНЕРГОСИСТЕМЫ. . . . . . . . . . . . . . . . | 42 |
| БИБЛИОГРАФИЧЕСКИЙ СПИСОК. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
| 48 | |
Б.Г. Булатов
МЕТОДЫ ПРИНЯТИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Дата: 2019-04-23, просмотров: 383.