Математическая модель – система переменных, а также уравнений и неравенств, которые описывают основные свойства системы и ее внутренние и внешние связи. Оптимизационная модель дополняется целевой функцией, которая формализует критерии оптимизации.
При составлении математических моделей для принятия решений при развитии энергетической отрасли широко используется эквивалентирование с тем, чтобы упростить модель.
· Применяется территориальное эквивалентирование, когда близко расположенные объекты объединяются в один. При этом появляется ошибка, связанная с учетом затрат на транспорт электроэнергии (потери, капитальные вложения и др.).
· Эквивалентирование внешних связей осуществляется, как правило, заданием объемов обмена ресурсами между смежными системами, с которыми связана рассматриваемая. При этом задача должна решаться итеративным методом, путем совместного планирования развития связанных систем.
· Эквивалентирование внутренних технологических связей осуществляется с помощью удельных расходов, например, топлива на выработку электроэнергии 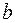 в т у.т. на МВт*ч. Разные технологии характеризуются разными удельными коэффициентами.
в т у.т. на МВт*ч. Разные технологии характеризуются разными удельными коэффициентами.
Исследуем более сложную по сравнению с моделью планирования производства линейную модель выбора структуры генерирующих мощностей для покрытия дефицита мощности в развивающейся энергосистеме (рисунок 3).
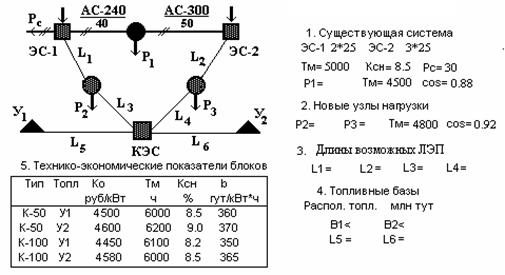
Рис. 3
Существующая система включает две ЭС и один нагрузочный узел, связанные с системой сетью 110 кВ. В перспективе планируется подключение двух новых нагрузок Р2 и Р3. Прогнозируемые нагрузки и длины возможных к сооружению новых ЛЭП задаются в соответствии с вариантом.
Для покрытия дефицита возможно сооружение новой КЭС на заданной площадке с блоками 50 и (или) 100 МВт. Поставка топлива для этой КЭС возможна от 2-х баз добычи У1 и У2 с заданными длинами транспортных магистралей. Прогнозируемые нагрузки в МВт, предельная мощность КЭС, длины возможных ЛЭП, предельные объемы выделяемого топлива В1 и В2 в млн. т у.т. в год, задаются по вариантам в таблице 5.
Таблица 5
| № | P1 | P2 | P3 | P пр | L1 | L2 | L3 | L4 | B1 | B2 | L5 | L6 |
| 1 | 70 | 80 | 77 | 300 | 54 | 51 | 48 | 56 | 0.3 | 0.2 | 340 | 350 |
| 2 | 60 | 75 | 85 | 200 | 46 | 57 | 60 | 59 | 0.2 | 0.24 | 350 | 410 |
| 3 | 75 | 80 | 65 | 200 | 56 | 59 | 37 | 58 | 0.32 | 0.15 | 420 | 390 |
| 4 | 60 | 75 | 90 | 200 | 40 | 50 | 57 | 45 | 0.3 | 0.4 | 250 | 300 |
| 5 | 80 | 67 | 80 | 250 | 45 | 58 | 62 | 40 | 0.2 | 0.3 | 270 | 320 |
| 6 | 70 | 80 | 79 | 300 | 54 | 51 | 48 | 66 | 0.31 | 0.2 | 300 | 350 |
| 7 | 60 | 90 | 80 | 200 | 46 | 50 | 60 | 52 | 0.2 | 0.2 | 350 | 400 |
| 8 | 75 | 88 | 69 | 250 | 55 | 45 | 47 | 56 | 0.33 | 0.15 | 450 | 370 |
Тарифы на добычу топлива в руб/т у.т. и его транспорт в руб/(т у.т.*км) приведены в таблице 6.
Таблица 6
| У1 | У2 | |
| Стоимость топлива С, руб/т у.т. | 1225.0 | 1195.0 |
| Стоимость транспорта Ст, руб/(т у.т.× км) | 1.30 | 1.10 |
Порядок выполнения работы
1. Определить дефицит мощности в системе с ориентировочным учетом потерь, расходов на с.н. и резерва.
2. Составить расчетную схему и определить состав переменных модели (рис.4).
3. Составить линейную оптимизационную модель выбора структуры генерирующих мощностей и новых ЛЭП системы, приняв Со=6,0 руб./(МВт*км) для существующих и Со=10 руб./(МВт*км) для новых ЛЭП.
4. В ограничениях модели учесть условия покрытия дефицита мощности, балансы мощности в узлах, ограничение по годовым объемам выделяемого топлива для каждой базы.
Ограничения модели, реализованные в решении, показанном на рис. 5, учитывают следующие свойства системы:
1- ограничение по предельной мощности КЭС,
2- условие покрытия дефицита мощности,
3,4- ограничения по топливу с баз У1 и У2,
5, 6, 7 – условия баланса мощности в узлах Р1, Р2 и Р3;
8- условие выдачи мощности в систему;
9, 10 – условия баланса на шинах ЭС-1 и ЭС-2;
11- условие баланса на шинах КЭС с четом расходов на с.н.;
12,13 –условия определения годовых расходов топлива с баз У1 иУ2.
В целевой функции учесть затраты на КЭС, в ЛЭП и на топливо с учетом его транспорта.
5. Активизировать программу Simple . exe и решить модель на ЭВМ симплекс-методом. Оценить влияние объемов выделяемого дефицитного топлива на решение.
6. По результатам решения выбрать схему развития системы и основное оборудование ( блоки, блочные трансформаторы и ЛЭП).
На рисунке 4 приведена расчетная схема системы, на которой отмечены выбранные переменные модели. Первые 4 определяют возможные установленные мощности в блоках разного типа при работе на топливе в объеме Х5 и Х6 с разных баз. Остальные переменные определяют возможные потоки по ЛЭП. На рисунке 5 показан вид экранной страницы с решением модели для расчетной схемы, приведенным на рис.4, где показаны и результаты расчета.
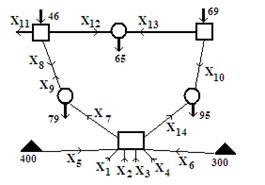
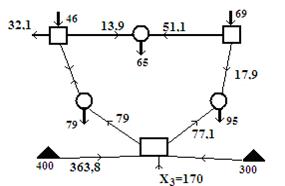
Рис.4
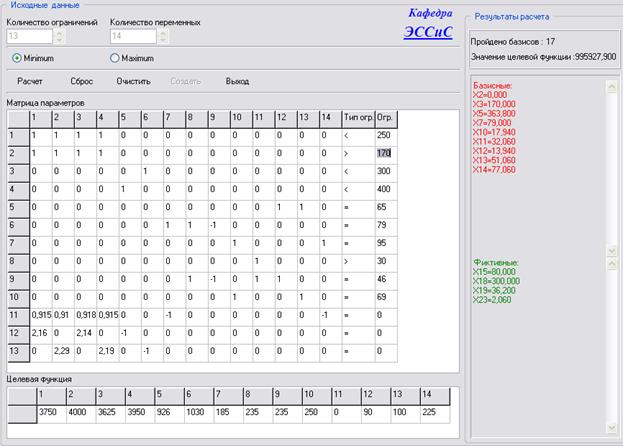
Рис.5
Контрольные вопросы
1. Признаки задач линейного программирования.
2. Геометрический смысл задачи.
3. В чем суть и идея симплекс-метода?
4. Какой смысл имеют фиктивные переменные?
5. Зачем и почему для некоторых линий вводят две переменные?
Лабораторная работа N 5
Математическая модель планирования развития сети
Цель работы: исследование методики составления оптимизационной модели с квадратичной функцией затрат при линейных ограничениях.
Дата: 2019-04-23, просмотров: 340.