Пусть f(x1, ..., x n)ÎP2, представим ее в виде формулы через конъюнкцию и сумму по модулю два, используя числа 0 и 1. Это можно сделать, так как {x1&x2, x1Åx2, 0, 1} полна в Р2. В силу свойства x& (yÅz) = xyÅ xz можно раскрыть все скобки, привести подобные члены, и получится полином от n переменных, состоящий из членов вида х 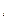 , х
, х 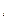 , ..., х
, ..., х 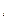 , соединенных знаком Å. Такой полином называется полиномом Жегалкина.
, соединенных знаком Å. Такой полином называется полиномом Жегалкина.
Общий вид полинома Жегалкина
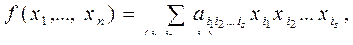
где 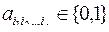 , s = 0, 1, ..., n, причем при s = 0 получаем свободный член а0.
, s = 0, 1, ..., n, причем при s = 0 получаем свободный член а0.
Представление функции в виде полинома Жегалкина
1. Представим любую функцию формулой над {x1&x2,  } и сделаем замену
} и сделаем замену 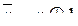 . Этот способ удобен, если функция задана формулой.
. Этот способ удобен, если функция задана формулой.
Пример 16. (x1 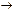 (x2
(x2 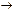 x3))(x1 Ú x2) x3 = (
x3))(x1 Ú x2) x3 = ( 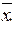 Ú
Ú 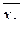 Ú x3)(x1 Ú x2) x3 =
Ú x3)(x1 Ú x2) x3 =
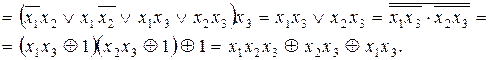
Надо помнить, что четное число одинаковых слагаемых в сумме по mod2 дает 0.
2. Метод неопределенных коэффициентов. Он удобен, если функция задана таблицей.
Пример 17. Запишем с неопределенными коэффициентами полином Жегалкина для функции трех переменных f(x1, x2, x3) = = (01101001) = а0Åа1х1Åа2х2Åа3х3Åb1x1x2Åb2x2x3Åb3x1x3Åcx1x2x3.
Затем находим коэффициенты, используя значения функции на всех наборах. f(0, 0, 0) = 0, с другой стороны, подставив набор (0, 0, 0) в полином, получим f(0, 0, 0) = а0, отсюда а0 = 0. f(0, 0, 1) = 1, подставив набор (0, 0, 1) в полином, получим f(0,0,1) = а0 Å а3, так как а0 = 0, отсюда а3 = 1. Aналогично f (0, 1, 0) = 1 =а2, f(0, 1, 1) = 0 = = а2 Å а3 Å b2 = b2 = 0; а1 = 1; 0 = а1 Å а3 Å b3 = b3 = 0; 0 = а1 Åа2 Å b1 = = b1 = 0; 1 = 1 Å 1 Å 1 Å c; c = 0; f(x1, x2, x3) = x1 Å x2 Å x3.
3. Многочлен Жегалкина можно получить также с помощью треугольника Паскаля по единицам его левой стороны по таблице следующим образом. Построим многочлен Жегалкина для функции
F = (10011110). Верхняя сторона треугольника есть функция f. Любой другой элемент треугольника есть сумма по модулю для двух соседних элементов предыдущей строки. Левая сторона треугольника для функции f содержит шесть единиц. Многочлен Жегалкина будет содержать шесть слагаемых. Первая единица треугольника соответствует набору (000). Первое слагаемое многочлена есть 1. Третья снизу единица в левой стороне треугольника соответствует набору (101). В качестве слагаемого многочлена берем x1x3. Aналогично для других единиц треугольника. Cлева от наборов показаны слагаемые многочлена Жегалкина (табл. 3.20).
Таблица 3.20
| N | x1x2x3 | f | Треугольник Паскаля | |
| 1 x3 x2 x2x3 x1 x1x3 x1x2 x1x2x3 | 000 001 010 011 100 101 110 111 | 1 0 0 1 1 1 1 0 | 1 0 0 1 1 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 1 0 1 | |
Тогда 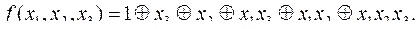
Теорема Жегалкина
Каждая функция из 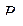 может быть представлена в виде полинома Жегалкина единственным образом.
может быть представлена в виде полинома Жегалкина единственным образом.
Здесь единственность понимается с точностью до порядка слагаемых в сумме и порядка сомножителей в конъюнкциях:
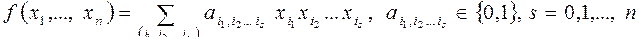 .
.
Доказательство. Любая функция из 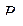 может быть представлена формулой над {x1&x2, x1Åx2, 0, 1}, а эта формула после раскрытия всех скобок и приведения подобных членов дает полином Жегалкина. Докажем единственность представления. Рассмотрим функции
может быть представлена формулой над {x1&x2, x1Åx2, 0, 1}, а эта формула после раскрытия всех скобок и приведения подобных членов дает полином Жегалкина. Докажем единственность представления. Рассмотрим функции 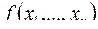 от
от 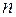 переменных. Мы знаем, что всего таких функций, т. е. их таблиц истинности,
переменных. Мы знаем, что всего таких функций, т. е. их таблиц истинности, 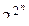 . Подсчитаем число различных полиномов Жегалкина от
. Подсчитаем число различных полиномов Жегалкина от 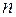 переменных. Число наборов
переменных. Число наборов 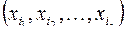 равно числу всех подмножеств множества
равно числу всех подмножеств множества  , сюда входит и пустое множество (если
, сюда входит и пустое множество (если  ). Число подмножеств множества из
). Число подмножеств множества из 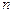 элементов равно
элементов равно 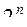 , а так как каждый набор входит с коэффициентом
, а так как каждый набор входит с коэффициентом 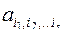 , принимающим два значения: 0 или 1, то число всевозможных полиномов будет
, принимающим два значения: 0 или 1, то число всевозможных полиномов будет 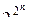 . Так как каждому полиному соответствует единственная функция, число функций от
. Так как каждому полиному соответствует единственная функция, число функций от 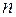 переменных равно числу полиномов, то каждой функции будет соответствовать единственный полином.
переменных равно числу полиномов, то каждой функции будет соответствовать единственный полином.
Определение. Функция 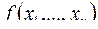 , полином Жегалкина для которой имеет следующий линейный относительно переменных вид:
, полином Жегалкина для которой имеет следующий линейный относительно переменных вид:
f = а0Å а1х1Å а2х2Å ... Åаn хn называется линейной.
Дата: 2019-04-23, просмотров: 315.