Минимизация нормальных форм

Минимальной ДНФ (МДНФ) функции f(x₁, ... , x _n) называется ДНФ, реализующая функцию f и содержащая минимальное число символов переменных по сравнению со всеми другими видами ДНФ, реализующими функцию f.

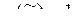Если для всякого набора = (a₁, ..., a _n) значений переменных условие  влечет 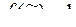, то функция g называется частью функции f (или функция f накрывает функцию g). Если при этом для некоторого набора  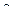= (c₁, ..., c _n) функция 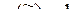, то говорят, что функция g накрывает единицу функции f на наборе  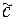(или что g накрывает конституенту единицы  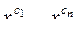функции f). Заметим, что конституента единицы функции f есть часть функции f, накрывающая единственную единицу функции f.

Элементарная конъюнкция K называется импликантом функции f, если для всякого набора = (a₁, ..., a _n) из 0 и 1 условие K( ) =1 влечет f( ) =1.

Импликант K функции f называется простым, если выражение, получающееся из него выбрасыванием любых множителей, уже не импликант функции f.

Ясно, что всякий импликант функции f есть часть функции f.

Теорема. Всякая функция реализуется дизъюнкцией всех своих простых имликант (ПИ).

Доказательство. Пусть f(x₁, ..., x _n) есть функция, а A = K₁v ... vK _m – дизъюнкция всех ее простых импликант. Пусть = (a₁, ..., a _n) – произвольный набор длины n из 0 и 1.

Если A( ) = 1, то найдется дизъюнктивное слагаемое K_i( ) = 1, что влечет f( ) = 1, ибо K_i есть импликант функции f.

Если f( ) = 1, то в СДНФ для функции f найдется элементарная конъюнкция K, равная на этом наборе единице. Один из простых имликантов K _j функции f получается выбрасыванием некоторых множителей из K и потому K _j ( ) = 1, а тогда A( ) = 1.

Cледовательно, f = A. Теорема доказана.

Сокращенная ДНФ функции f есть дизъюнкция всех простых импликант функции f. Всякая функция f реализуется своей сокращенной ДНФ. Для всякой функции, не равной тождественно нулю, существует единственная сокращенная ДНФ.

Пусть A и B – произвольные формулы. Из свойств булевых операций вытекают следующие обратимые правила преобразования ДНФ:

1) 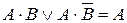 – полное склеивание (развертывание);

2) 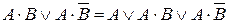 – неполное склеивание;

3)  – обобщенное склеивание;

4) 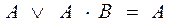– поглощение;

5) 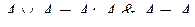– идемпотентность (удаление дублирующих членов).

Теорема (Квайна). Если в CДНФ функции f провести все операции неполного склеивания, а затем все операции поглощения и удаления дублирующих членов, то в результате получится сокращения ДНФ функции f.

Доказательство. Пусть имеем сокращенную ДНФ функции f. Проведем все операции развертывания к каждому простому импликанту для получения недостающих переменных в каждом дизъюнктивном слагаемом сокращенной ДНФ. В полученном выражении из нескольких одинаковых дизъюнктивных слагаемых оставим только по одному экземпляру. В результате получим CДНФ функции f. Теперь, исходя из полученной CДНФ, в обратном порядке проведем операции добавления одинаковых дизъюнктивных слагаемых (с помощью правил идемпотентности), неполного склеивания и поглощения. В итоге получим исходную сокращенную ДНФ.