Обозначения: E2={0,1}; Е 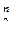 = E2 ´ E2 ´ ... ´ E2 – прямое произведение n сомножителей; (x
= E2 ´ E2 ´ ... ´ E2 – прямое произведение n сомножителей; (x 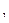 , ..., xn)Î
, ..., xn)Î 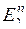 , |E2| – мощность E2, |E2| = 2, тогда |Е
, |E2| – мощность E2, |E2| = 2, тогда |Е 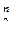 | = 2n.
| = 2n.
Определение. Функцией алгебры логики называется отображение Е 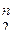 ÞE2 , причем отображение всюду определено и функционально.
ÞE2 , причем отображение всюду определено и функционально.
Так как множество Е 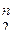 конечно, то задать отображение Е
конечно, то задать отображение Е 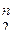 ÞE2 означает задать множество наборов из Е
ÞE2 означает задать множество наборов из Е 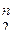 и для каждого набора указать его образ в Е2.
и для каждого набора указать его образ в Е2.
Пример 1. Пусть 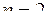 , тогда Е
, тогда Е 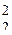 = {(0 0), (0 1), (1 0), (1 1)}, отображение Е
= {(0 0), (0 1), (1 0), (1 1)}, отображение Е 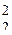 ÞE2 задано, например, так: (0 0)Þ0; (0 1)Þ1; (1 0)Þ1; (1 1)Þ1. Тем самым задана функция, для которой мы будем использовать стандартное обозначение f(x1, x2), записывая эту функцию в виде табл. 3.1.
ÞE2 задано, например, так: (0 0)Þ0; (0 1)Þ1; (1 0)Þ1; (1 1)Þ1. Тем самым задана функция, для которой мы будем использовать стандартное обозначение f(x1, x2), записывая эту функцию в виде табл. 3.1.
Таблица 3.1
| x1 | x2 | f(x1, x2) |
| 0 0 1 1 | 0 1 0 1 | 0 1 1 1 |
Здесь x1 и x2 обозначают названия столбцов, а f – символ, обозначающий отображение. Следует обратить внимание, что функции f (x1, x2) и f (y1, y2) задают одно и то же отображение и их таблицы отличаются только названиями столбцов.
Определение. Таблица, задающая функцию f(x 1, x 2, ..., x n), называется таблицей истинности для этой функции.
Рассмотрим функции одной переменной. Их будет всего 4, они задаются таблицами истинности 3.2–3.5:
Таблица 3. 2
| x | f0(x) |
| 0 1 | 0 0 |
Функция называется константой 0, записывается f0(x) 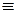 0.
0.
Таблица 3. 3
| x | f1(x) |
| 0 1 | 0 1 |
Функция называется тождественной, записывается f1(x) = x.
Таблица 3. 4
| x | f2(x) |
| 0 1 | 1 0 |
Функция называется «не x» и записывается 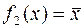 .
.
Таблица 3.5
| x | f3(x) |
| 0 1 | 1 1 |
Функция записывается f3(x)  1 и называется константой 1.
1 и называется константой 1.
Если стандартным расположением переменной x считать 0 в первой строке и первом – во второй, то функции f0, f1, f2, f3 определяются однозначно наборами значений: f0 =(0,0), f1 =(0,1), f2 = (1,0) и f3 = (1,1). Наборы значений функций составляют множество E2 ´ Е2, поэтому количество функций одной переменной равно |E2 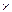 E2|=4. Для удобства функции пронумерованы так, что двоичный код номера совпадает с набором значений функции.
E2|=4. Для удобства функции пронумерованы так, что двоичный код номера совпадает с набором значений функции.
Рассмотрим функции двух переменных f (x1, x2). Функции двух переменных определены на множестве Е 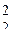 ={(0 0), (0 1), (1 0), (1 1)}, эти наборы переменных из Е
={(0 0), (0 1), (1 0), (1 1)}, эти наборы переменных из Е 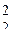 можно тоже рассматривать как двоичные коды чисел 0, 1, 2, 3. Именно такой порядок расположения наборов (x1, x2) будем считать стандартным. Тогда функции f (x1, x2) определяются однозначно наборами значений (b1, b2, b3, b4), где каждое biÎE2, поэтому (b1, b2, b3, b4)ÎЕ
можно тоже рассматривать как двоичные коды чисел 0, 1, 2, 3. Именно такой порядок расположения наборов (x1, x2) будем считать стандартным. Тогда функции f (x1, x2) определяются однозначно наборами значений (b1, b2, b3, b4), где каждое biÎE2, поэтому (b1, b2, b3, b4)ÎЕ 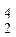 . Следовательно, число функций двух переменных равно 24 = 16, занумеруем их числами от 0 до 15 так, чтобы двоичный код номера совпадал с набором значений функции (табл. 3.6).
. Следовательно, число функций двух переменных равно 24 = 16, занумеруем их числами от 0 до 15 так, чтобы двоичный код номера совпадал с набором значений функции (табл. 3.6).
Таблица 3. 6
| x1x2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
| 0 0 0 1 1 0 1 1 | 0 0 0 0 | 0 0 0 1 | 0 0 1 0 | 0 0 1 1 | 0 1 0 0 | 0 1 0 1 | 0 1 1 0 | 0 1 1 1 | 1 0 0 0 | 1 0 0 1 | 1 0 1 0 | 1 0 1 1 | 1 1 0 0 | 1 1 0 1 | 1 1 1 0 | 1 1 1 1 |
Некоторые из этих функций носят специальные названия и играют такую же роль, как элементарные функции в анализе, поэтому называются элементарными функциями алгебры логики. Перечислим их.
1) f1(x1, x2) = (x1& x2), читается «конъюнкция х1 и х2», иногда вместо знака & употребляют знак 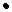 или вообще его опускают, пишут (х1x2). Конъюнкция совпадает с обычным произведением х1х2 и совпадает с min(x1, x2). Эту операцию называют также логическим умножением.
или вообще его опускают, пишут (х1x2). Конъюнкция совпадает с обычным произведением х1х2 и совпадает с min(x1, x2). Эту операцию называют также логическим умножением.
2) f6(x1, x2) = (x1Å x2) – сложение х1 и x2 по модулю два, иногда пишут (х1+ x2)mod2.
3) f7(x1, x2) = (x1Úx2), читается «x1 дизъюнкция x2», она совпадает с max(x1, x2), ее называют логическим сложением.
4) f8(x1, x2) = (x1 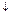 x2), читается «x1 стрелка Пирса x2» и совпадает с отрицанием дизъюнкции, другие названия: функция Вебба, функция Даггера.
x2), читается «x1 стрелка Пирса x2» и совпадает с отрицанием дизъюнкции, другие названия: функция Вебба, функция Даггера.
5) f9(x1, x2) = (x1~ x2), читается «х1 эквивалентно x2».
6) f13(x1, x2) = (x1 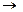 x2), читается «х1 импликация x2», иногда обозначается
x2), читается «х1 импликация x2», иногда обозначается 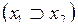 , т. е. х1 влечет x2.
, т. е. х1 влечет x2.
7) f14(x1, x2) = (x1|x2), читается «х1 штрих Шеффера x2», она является отрицанием конъюнкции.
Cимволы  , &, Ú,
, &, Ú,  , ~,
, ~,  , Å, |, участвующие в обозначениях элементарных функций, называются логическими связками или просто связками. Переменные 0 и 1 называются логическими или булевыми переменными, причем 0 соответствует «лжи», а 1 –«истине», а функции алгебры логики называются еще и булевыми функциями.
, Å, |, участвующие в обозначениях элементарных функций, называются логическими связками или просто связками. Переменные 0 и 1 называются логическими или булевыми переменными, причем 0 соответствует «лжи», а 1 –«истине», а функции алгебры логики называются еще и булевыми функциями.
Рассмотрим функцию f(x1...x n), где (x1...x n)ÎЕ 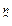 , тогда число наборов (x1...x n), где функция f(x1...x n) должна быть задана, равно |Е
, тогда число наборов (x1...x n), где функция f(x1...x n) должна быть задана, равно |Е 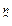 |=2n. Обозначим множество всех функций двузначной алгебры логики Р2. Обозначим через Р2(n) число функций, зависящих от n переменных. Очевидно,
|=2n. Обозначим множество всех функций двузначной алгебры логики Р2. Обозначим через Р2(n) число функций, зависящих от n переменных. Очевидно, 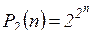 .
.
C ростом n число Р2(n) быстро растет: P2(1) = 4, P2(2) = 16, P2(3) = 256, P2(4) = 65536. При больших n табличный способ задания функций становится неприемлемым, используется формульное задание функций. Но прежде чем ввести понятие формулы, дадим определение существенной переменной.
Определение. Функция f(x1, ..., x i–1, x i, x i +1, ..., x n) существенно зависит от переменной х i , если существуют такие значения a1, ... ai–1, ai+1, ..., an переменных x 1, ..., x i–1, x i+1, ..., x n, что
f(a1, ..., ai–1, 0, ai+1, ..., an) ¹ f(a1, ..., ai–1, 1, ai+1, . . ., an).
Тогда переменная х i называется существенной переменной. В противном случае х i называется фиктивной переменной.
Пример 2. Рассмотрим несколько функций двух переменных (табл. 3.7).
Таблица 3.7
| x1 | x2 | (x1&x2) | f3 | f15 |
| 0 0 1 1 | 0 1 0 1 | 0 0 0 1 | 0 0 1 1 | 1 1 1 1 |
Покажем, что (x1&x2) существенно зависит от х1. Рассмотрим наборы (0, 1) и (1, 1), здесь a2 = 1, f(0, a2) = 0 и не равно f(1, a2) = 1. Покажем, что x2 – тоже существенная переменная. Рассмотрим наборы (1, 0) и (1, 1). Здесь a1 = 1, f(1, 0) = 0 и не равно f(1, 1) = 1. Для функции f3(x1, x2) покажем, что х2 – фиктивная переменная, т. е. надо показать, что не существует наборов (a1, 0) и (a1, 1) таких, что f3(a1, 0) 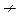 f3(a1, 1). Пусть a1 = 0, т. е. рассмотрим наборы (0, 0) и (0, 1), f(0, 0) = f(0, 1) = 0. Пусть a1=1, но f (1, 0) = f(1, 1) = 1.
f3(a1, 1). Пусть a1 = 0, т. е. рассмотрим наборы (0, 0) и (0, 1), f(0, 0) = f(0, 1) = 0. Пусть a1=1, но f (1, 0) = f(1, 1) = 1.
Для функции f15x1 и x2 являются фиктивными переменными: x1 – фиктивная переменная, так как не существуют наборы (0, a2) и (1, a2) такие, что f (0, a2)¹f (1, a2). Если a2 = 0, то f (0, 0) = f (1, 0)=1, если a2 = 1, тогда f (0, 1) = f (1, 1) = 1. Aналогично доказывается, что 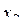 тоже фиктивная переменная.
тоже фиктивная переменная.
Пусть х i является фиктивной переменной для функции f(x1, ..., xi, ..., x n). Тогда ее можно удалить из таблицы истинности, вычеркнув все строки вида (a1, ..., ai–1, 1, ai+1, ..., an) или, наоборот, все строки вида (a1, ..., ai–1, 0, ai+1, ..., an) и столбец для переменной х i. При этом получим таблицу для некоторой функции g(x1, ..., xi–1, xi+1, ..., x n). Будем говорить, что функция g(x1, ..., x i–1, x i+1, ..., x n) получена из функции f(x1, ..., xi, ..., x n) путем удаления фиктивной переменной хi или f получена из g путем введения фиктивной переменной х i (табл. 3.8).
Определение. Функции f1 и f2 называются равными, если f2 можно получить из f1 путем добавления или удаления фиктивной переменной.
Пример 3.
Таблица 3.8
| x1 | x2 | f3 |
| 0 0 1 1 | 0 1 0 1 | 0 0 1 1 |
Вычеркнув строки типа (a, 1), т. е. (0, 1) и (1, 1) и столбец для х2,. получим f3 (x1x2) = g(x1) = x1.
Пример 4. Пусть функция g(x1x2) задана в табл. 3.9 и существенно зависит от обеих переменных.
Таблица 3.9
| x1 | x2 | g |
| 0 0 1 1 | 0 1 0 1 | 0 0 0 1 |
Построим функцию f(x1, x2, x3), которая получается из g(x1, x2) введением фиктивной переменной х3 (табл. 3.10).
Таблица 3. 10
| x1 | x2 | x3 | 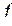
|
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 0 0 0 0 0 0 1 1 |
К наборам (x1, х2) мы добавим х3 = 0, получим наборы вида (a1, a2, 0), на этих наборах функцию f положим равной g(a1, a2), затем добавим наборы вида (a1, a2, 1), функцию f(a1, a2, 1) положим равной g(a1, a2).
Особую роль играют константы 0 и 1, которые не имеют существенных переменных и которые можно рассматривать как функции от пустого множества переменных.
3.2. Формульное задание функций алгебры логики
Дадим индуктивное определение формулы над множеством. Это определение несколько сложное по форме, но будет полезно в дальнейшем. С индуктивным определением мы встречались в математическом анализе при определении n-го дифференциала 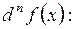 было введено понятие первого дифференциала
было введено понятие первого дифференциала 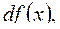 а затем n-й дифференциал определялся как первый дифференциал от
а затем n-й дифференциал определялся как первый дифференциал от 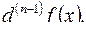
Определение. Пусть 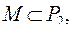 тогда:
тогда:
1) каждая функция 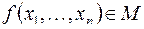 называется формулой над
называется формулой над 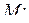
2) пусть 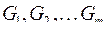 – либо переменные, либо формулы над
– либо переменные, либо формулы над 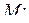
3) если 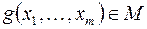 , то
, то 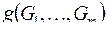 – называется формулой над M.
– называется формулой над M.
Формулы будем обозначать заглавными буквами: 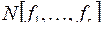 , имея в виду функции, участвовавшие в построении формулы, или
, имея в виду функции, участвовавшие в построении формулы, или 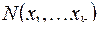 имея в виду переменные, вошедшие в формулу.
имея в виду переменные, вошедшие в формулу.
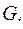 – формулы, участвовавшие в построении
– формулы, участвовавшие в построении 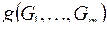 , называются подформулами.
, называются подформулами.
Пример 5. Пусть 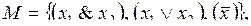 тогда
тогда 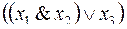 – формула над M.
– формула над M.
Cопоставим каждой формуле 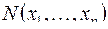 функцию
функцию 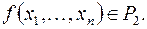 Cопоставление будем производить в соответствии с индуктивным определением формулы.
Cопоставление будем производить в соответствии с индуктивным определением формулы.
1) Пусть 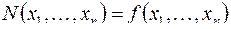 тогда формуле
тогда формуле 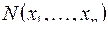 сопоставим функцию
сопоставим функцию 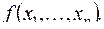
2) Пусть 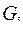 – формула над M и пусть ей по индуктивному предположению сопоставлена функция
– формула над M и пусть ей по индуктивному предположению сопоставлена функция 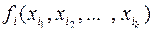 . Если
. Если 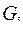 – переменная, т. е.
– переменная, т. е. 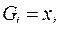 , то ей сопоставим функцию
, то ей сопоставим функцию 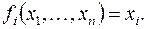
Таким образом, каждой подформуле 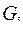 сопоставлена функция
сопоставлена функция
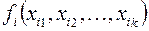 , где каждая функция зависит от своих переменных и их число может быть различным. Но
, где каждая функция зависит от своих переменных и их число может быть различным. Но 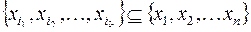 переменных, перечисленных в формуле
переменных, перечисленных в формуле 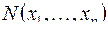 . В каждую функцию
. В каждую функцию 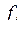 введем недостающие переменные (они будут фиктивными), получим, что каждой подформуле
введем недостающие переменные (они будут фиктивными), получим, что каждой подформуле 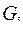 сопоставлена функция
сопоставлена функция 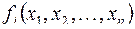 .
.
3) Тогда
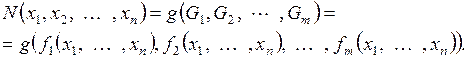
Cопоставим формуле 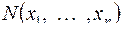 функцию
функцию 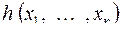 следующим образом: пусть
следующим образом: пусть 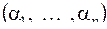 – произвольный набор переменных, пусть
– произвольный набор переменных, пусть 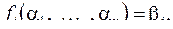 тогда
тогда 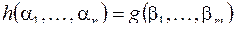
Множество всех формул над M обозначим через <M>.
Определение. Две формулы N и D из <M> называются равными N = D или эквивалентными N ~ D, если функции, реализуемые ими, равны.
Упрощение записи формул:
1) внешние скобки можно опускать;
2) приоритет применения связок возрастает в следующем порядке: ~, 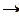 , Ú, &;
, Ú, &;
3) связка  над одной переменной сильнее всех связок;
над одной переменной сильнее всех связок;
4) если связка  стоит над формулой, то сначала выполняется формула, затем отрицание;
стоит над формулой, то сначала выполняется формула, затем отрицание;
5) если нет скобок, то операции ~ и 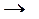 выполняются в последнюю очередь.
выполняются в последнюю очередь.
Пример 6. Доказать эквивалентность формул (табл. 3.11).
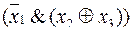 ~ (
~ ( 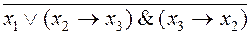 ) .
) .
Таблица 3.11
| x1 | x2 | x3 | x2Åx3 | & 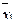
| x2 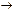 x3 x3
| x3 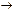 x2 x2
| & | Úx1 | – |
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 0 1 1 0 0 1 1 0 | 0 1 1 0 0 0 0 0 | 1 1 0 1 1 1 0 1 | 1 0 1 1 0 0 1 1 | 1 0 0 1 1 0 0 1 | 1 0 0 1 1 1 1 1 | 0 1 1 0 0 0 0 0 |
Дата: 2019-04-23, просмотров: 320.