Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Определение. Говорят, что множество А включено в множество В (и пишут АÍВ или ВÊА), если для любого элемента аÎА справедливо аÎВ.

Например, очевидны следующие включения NÍZÍQÍR.

Cвойства:

1) для любого множества А справедливо включение АÍА;

2) если АÍВ и ВÍА, то А = В;

3) если АÍВ и ВÍС, то АÍС;

4) для любого множества А справедливо включение ÆÍА.

Доказательство. Приведем доказательство лишь одного – четвертого свойства. Предположим противное, что Æ не включено в множество А. Это означает, что должно существовать хÎÆ такое, что хÏА. Но для любого х справедливо хÏÆ. Cледовательно такого х не существует и ÆÍА.

Замечание. Необходимо различать символ принадлежности Î и символ включения Í. Cимвол принадлежности не обязан удовлетворять тем же свойствам что и символ включения. Так, например, 1ÎZ, ZÎ{Z}, однако 1Ï{Z}.

Операция «объединение множеств». Пусть А и В два множества. Объединением этих множеств называется множество АÈВ, состоящее из тех элементов, которые принадлежат хотя бы одному из множеств А или В:

АÈВ = {x: хÎА либо хÎВ}.

Операция «разность множеств». Для множеств А и В разность множеств А – В состоит из тех и только тех элементов х, которые удовлетворяют следующим двум условиям хÎА и хÏВ:

А – В = {х: хÎА и хÏВ}.

Операция «пересечение множеств». Для множеств А и В их пересечением АÇВ называется множество таких элементов х, которые принадлежат как A, так и В:

АÇВ = {х: хÎА и хÎВ}.

Операция «симметрическая разность множеств». Для множеств А и В их симметрической разностью называется множество

АDВ = (А – В)È(В – А).

Наиболее часто нами будут использоваться операции объединения и пересечения. Они могут быть распространены на любое число множеств (так же как и другие операции):

È_aÎI А = {х: $aÎI: хÎА_a },

Ç_aÎI А = {х: "aÎI: хÎА_a }.

В случае, когда множество индексов I = N, применяется запись вида È_n . Например,

если А _n = (–1/n, 1/n ), то Ç_n А_n = {0}.

Если ВÍА, то разность множеств А – В называют еще дополнительным множеством к В или просто дополнением в А и обозначают В ^C .

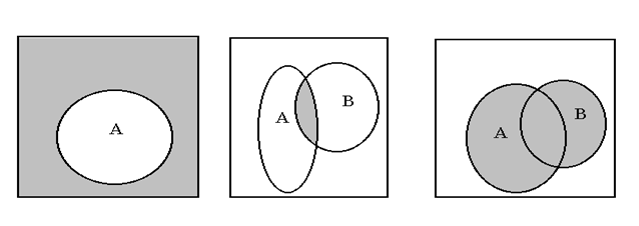
Операции над множествами хорошо иллюстрируются диаграммами Венна (рис. 1.1, 1.2, 1.3).

Рис. 1.1. Заштриховано дополнительное множество к множеству А	Рис. 1.2. Заштриховано пересечение множеств А и В	Рис. 1.3. Заштриховано объединение множеств А и В

 

Теорема 1. Для любых множеств A, B, C, D справедливы равенства:

 

1. AÈ(BÈC) = (AÈB)ÈC	1'. AÇ(BÇC) = (AÇB)ÇC
2. AÈB = BÈA	2'. AÇB = BÇA
3. AÈ(BÇC) = (AÈB)Ç(AÈC)	3'. AÇ(BÈC) = (AÇB)È(AÇC)
4. АÈА = А	4'. АÇА = А
5. AÈÆ = A, AÈD = D (при условии A Í D)	5'. AÇÆ = Æ, AÇD = A (при условии AÍD)
6. AÈ(D – A) = D	6'. AÇ(D – A) = Æ

 

(Некоторые из приведенных выше свойств имеют специальные названия: 1 и 1' – свойства ассоциативности, 2 и 2' – коммутативности, 3 и 3' – дистрибутивности, 4 и 4' ‒ идемпотентности).

Доказательство. Приведем доказательство свойств 3 и 5' (остальные доказываются просто или аналогично). Начнем со свойства 3. В силу одного из свойств операции включения (свойство 2), достаточно показать, что множество справа включено в множество, стоящее слева, и наоборот. Пусть хÎAÈ(BÇC). Тогда либо хÎA, либо хÎBÇC. Если хÎA, то хÎAÈB и хÎAÈC, т. е. хÎ(AÈB)Ç(AÈC). Если же хÎBÇC, то хÎB и хÎC. Cледовательно хÎAÈB и хÎAÈC, т. е. снова хÎ(AÈB)Ç(AÈC). Этим показано включение AÈ(BÇC)Í(AÈB)Ç(AÈC). Наоборот, если хÎ(AÈB)Ç(AÈC), то хÎAÈB и хÎAÈC. Если хÎA, то хÎAÈ(BÇC). Если же хÏA, то обязательно хÎB и хÎC. Cледовательно хÎBÇC и хÎAÈ(BÇC), что и доказывает утверждение.

Докажем свойство 5'. Из свойства 4 операции включения имеем ÆÍAÇÆ. Покажем обратное включение. Предположим противное, что AÇÆ не включено в Æ. Тогда существует хÎAÇÆ, т. е. хÎA и хÎÆ, такое, что хÏÆ. Но здесь написаны две противоречивые принадлежности. Это доказывает, что наше исходное предположение не верно и AÇÆÍÆ. Аналогично показывается и вторая часть рассматриваемого свойства.

В случае, когда все рассматриваемые множества заведомо принадлежат одному и тому же множеству U, это множество называют универсумом.

Операции над множествами, хотя и являются похожими на операции сложения (объединение), вычитания (разность множеств), и умножения (пересечение) над обычными числами, отличны от них по своим свойствам. Так, например, (А – В)ÈВ = А верно не всегда (приведите пример).

Другим существенным отличием являются так называемые законы поглощения: для множеств из универсума U справедливы равенства:

1. АÈ(АÇВ) = А;

2. АÇ(АÈВ) = А;

3. АÈ(А^СÇВ) = АÈВ.

Доказательства этих равенств несложные и опираются на теорему 1. Так первое из них получается из следующих равенств:

АÈ(АÇВ) = (АÇU)È(AÇB) = AÇ(UÈB) = AÇU = A.

Для множеств из универсума U справедливы следующие два закона де Моргана.

Теорема 2. Справедливы равенства:

(АÈВ)^С = А ^СÇ В ^С и (АÇВ)^С = А ^СÈ В ^С.

Доказательство. Докажем первое из этих равенств. Пусть аÎ(АÈВ)^С. Тогда аÏАÈВ, т. е. аÏА и аÏВ. Последнее означает, что аÎА^С и аÎВ^С , а значит и аÎА^СÇ В ^С . Цепочку этих рассуждений легко теперь провести в обратном порядке.

Второе равенство доказывается по аналогии.

На законах де Моргана основан принцип двойственности, играющий важную роль в теории множеств и ее приложениях. Принцип двойственности состоит в следующем: если в некотором равенстве, связывающем подмножества данного универсума, заменить операцию Ç на È, а Ç на È, множество U на Æ, множество Æ на U, то получим верное равенство. Новое равенство называется двойственным по отношению к заданному.

Примеры. 1) АÈÆ = АÞ(АÈÆ)^С = А ^СÞА^СÇÆ^С = А ^СÞА^СÇU = А ^С. Последнее равенство в силу произвольности А (а следовательно и А ^С ) можно переписать ВÇU = В для любого множества В из U.

2) (задача Льюиса Керролла). В одном жестоком бою из 100 пиратов 70 потеряли ногу, 75 – руку, 80 – глаз, 85 – ухо. Доказать, что как минимум 10 человек потеряли и руку, и ногу, и глаз, и ухо.

Решение. Обозначим через А – множество пиратов, потерявших ногу, В – потерявших руку, С – глаз, Е – ухо. Тогда нам необходимо найти М = АÇВÇСÇЕ (точнее, показать, что там не менее 10 элементов). Рассмотрим М ^С = А ^СÈВ^СÈС^СÈЕ^С. По условиям задачи в множестве А ^С – 30 элементов, в множестве В ^С – 25, С ^С – 20, Е ^С – 15. Таким образом, в множестве М ^С не более чем 30 + 25 + 20 + 15 = 90 элементов. Следовательно, в самом множестве М не менее чем 10 элементов.

 

Задачи.

1. Доказать следующие утверждения:

а) из АÍВ вытекает, что АÇВ = А и АÈВ = В;

б) из АÇВ = А вытекает, что АÍВ;

в) из АÈВ = В вытекает, что АÍВ.

2. Доказать:

а) АÈ(ВÇС) = (АÈВ)Ç(АÈС);

б) АÇ(ВÈС) = (АÇВ)È(АÇС).

3. Доказать включения:

а) (АÇС)È(ВÇD)Í(АÈВ)Ç(СÈD);

б) (В – С) – (В – А)ÍА – С;

в) А – СÍ(А – В)È(В – С).

4. Доказать: АDВ = (АÈВ) – (АÇВ).

5. Верны ли утверждения для любых множеств А, В, С: 1) если АÍВ и ВÎС, то АÎС; 2) если А ¹ В и В ¹ С, то А ¹ С?

6. При каких условиях на А и В выполняется равенство
(А – В)ÈВ = А.

7. Пусть U = {a, b, c, d, e, f} – универсум, A = {a, b, c},
B = {a, c, e, f}, C = {d, e, f}. Найти А – В, В – С, С – В, А – С, А^CÈВ, ВÇА^C, АÇС, СDА.

8. Пусть АÇВ = Æ. Что можно сказать про множества А – В и
В – А.

9. Пусть АÇВ^С = Æ. Что можно сказать про множества АÇВ и АÈВ.

10. Доказать равенства:

а) (А – В) – С = (А – С) – (В – С);

б) (А – В)È(В – С)È(С – А)È(АÇВÇС) = АÈВÈС;

в) А – В = А – (АÇВ) = (АÈВ) – В;

 

г) А – (А – В) = А Ç В;

д) А – (ВÈС) = (А – В)Ç(А – С);

е) А – (ВÇС) = (А – В)È(А – С);

ж) (АÈВ) – С = (А – С)È(В – С).

11. Вытекает ли из А – В = С, что А = ВÈС?

12. Вытекает ли из А = ВÈС, что А – В = С?

13. Пусть А – заданное множество, про другое множество Х известно, что АDХ = А. Доказать, что Х = Æ.

14. Доказать равенства:

а) АD(ВDD) = (АDВ)DD;

б) АÇ(ВDD) = (АÇВ)D(АÇD);

в) АDА = Æ;

г) АDÆ = А.

15. Доказать следующие тождества:

а) (АÇВ)È(СÇD) = (АÈС)Ç(ВÈС)Ç(АÈD)Ç(ВÈD);

б) (АÈВ)ÇА = (АÇВ)ÈА = А;

в) А – (В – С) = (А – В)È(АÇС);

г) АÇ(В – С) = (АÇВ) – (АÇС) = (АÇВ) – С;

д) АÈВ = АÈ(В – А);

е) (А ^С)^С = А;

ж) АÈА^С = U;

з) АÇА^С = Æ;

и) [А ^СÈВ]ÇА = АÇВ;

к) АÇ(В-А) = Æ;

л) А – (ВÈС) = (А – В) – С.

16. Доказать, что

а) (АÈВ)ÇС = АÈ(ВÇС) Û АÍС;

б) А = ВÛАDВ = Æ;

в) АÇВ = АÈ ВÛА = В;

г) (АÈВ) – В = АÛАÇВ = Æ;

д) (А – В)ÈВ = АÛВÍА;

е) (АÇВ)ÈС = АÇ(ВÈС)ÛСÍА;

ж) АÍВ Þ АÈСÍВÈС;

з) АÍВ Þ АÇСÍВÇС;

и) АÍВ Þ (С – В) Í(С – А);

к) АÍВ Þ В^СÍА^С;

л) А = В^С Û АÇВ=Æ и АÈВ = U.

17. Доказать тождества:

а) АÈВ = АÈВÈ(АÇВ);

б) А – В = А – (АÇВ);

в) АÈÆ = А;

г) А – А = Æ;

д) ADU = A^C;

е) АDВ = (АÈВ) – (АÇВ);

18.  Пусть AÍU, BÍU. Доказать:

а) A – B = A Ç B^C;

б) ADB = (A Ç B^C) È (A^CÇ B).

19. Решить систему уравнений

а)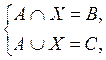

где А, В, С – данные множества и ВÍАÍС.

б)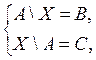

где А, В, С – данные множества и ВÍА, АÇС = Æ.

в)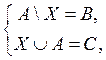

где А, В, С – данные множества и ВÍАÍС.

20. Определить операции È, Ç, \ через:

а) Ç и D;

б) D и È;

в) \ и D.

21. Доказать, что для любых множеств E, F, G, H справедливы включения:

а) ED(FÈG)Ì(EDF)È(EDG);

б) ED (F – G)Ê(FDE) – (GDE);

в) (EDF)Ç(GDH)Ì(EÇG)D(FÇH);

г) (EDF) – (GDH)Ì[ED(F – H)]È[(E – G)D(FÇH)];

д) ED(FÇG)É(EDF)Ç(EDG);

е) (FÇE)D(GÇH)Í(GDE)È(FDH).

22. Cправедливо ли равенство

(АDВ)Ç(СDD) = (АÇС)D(ВÇD)?

23. Cправедливо ли равенство

(АDВ)È(СDD) = (АÈС)D(ВÈD)?