Определение. Если для двух множеств A и В существует биекция A на В, то говорят что они имеют равную мощность. Если же существует инъекция множества A на В и не существует биекции между ними, то говорят, что мощность множества A меньше мощности множества В.

Первый зародыш общего понятия равномощности появляется у Галилея, заметившего, что отображение 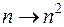 устанавливает биекцию между натуральными числами и их квадратами. Этот пример был приведен Галилеем в качестве контрпримера к «аксиоме»: «целое больше части». Понятие равномощных множеств было введено Больцано.

Мощность множества, кардинальное число (от слова cardinalis – главный) Кантор определил так: свойство множества, которое остается после абстрагирования от качества элементов множества и от их порядка. Мощность множества A мы будем обозначать card(A) (иногда его обозначают |A|). По определению, если множества A и В равномощны, то пишут card(A) = card(B). Если же мощность множества A меньше мощности В, то соответственно пишут card(A)<card(B). В этом случае, согласно определению, множество A равномощно некоторой части множества В.

Если рассмотреть отношение «иметь равную мощность» на множестве всех множеств, то нетрудно проверить, что оно является отношением эквивалентности.

Два конечных множества являются равномощными только в том случае, когда они имеют одинаковое количество элементов.

В случае, когда в конечном множестве A содержится n элементов, говорят, что его мощность равна n и пишут card(A) = n.

Теорема 1. Для конечных множеств справедливы равенства:

а) если AÇВ = Æ, то card(AÈВ) = card(A) + card(B);

б) если AÇВ ¹Æ, то card(AÈВ) = card(A) + card(B) – card(AÇB).

Доказательство. Осуществляется прямым счетом элементов множества AÈВ. В случае а) из хÎAÈВÞ либо хÎA и хÏВ, либо хÏA и хÎВ. Из этого уже следует утверждаемое. В случае же б) множество AÈВ можно разбить на следующие части: элементы хÎA и хÏВ, элементы хÎВ и хÏA и, наконец элементы хÎA и хÎВ.

Следствие . Если AÍВ, то card(B – A) = card(B) – card(A).

Теорема 2. Для конечных множеств справедливо равенство

card(A´B) = card(A)´card(B).

Доказательство. Пусть A = {а₁, а₂, ..., а_n} и В = {b₁, b₂, ..., b _m}. Тогда A´В = {(а _i, b_j): i = 1, 2, ..., n; j =1, 2, ..., m} = {(а₁, b₁), (а₁, b₂), ..., (а₁, b_m)}È{(а₂, b₁), (а₂, b₂), ..., (а₂, b_m)}È...È{(а _n, b₁), (а _n, b₂), ..., (а _n, b_m)}. Каждое из множеств, входящих в выписанное объединение, не пересекается с остальными и содержит точно m элементов. Всего множеств в объединении n штук. По предыдущей теореме получаем необходимое равенство.

Следствие. Справедливо равенство card(A ⁿ) = (card(A))ⁿ.

Задача. Известно, что из 100 студентов живописью увлекается 28 человек, спортом – 42 человека, музыкой – 30, живописью и спортом – 10, живописью и музыкой – 8, спортом и музыкой – 5, живописью, спортом и музыкой – 3. Найти количество студентов, занимающихся только спортом; не увлекающихся ничем.

Решение. Обозначим первой большой буквой множество студентов, увлекающихся тем или иным видом (например, Ж – множество студентов, увлекающихся живописью). Множество всех студентов обозначим через U. Тогда нас интересует card(С – (ЖÈМ)) и card(U – (ЖÈМÈС)). Из теоремы 1 и ее следствия, свойств операций над множествами имеем:

card(С – (ЖÈМ)) = card(С – ((ЖÈМ)Ç С))) = card(С) –

– card((ЖÇ С)È(МÇС)) = card(С) – (card(ЖÇ С) + card(МÇC) –

– card(ЖÇМÇC)) = 42 – (10 + 5 – 3) = 30.

card(U – (ЖÈМÈC)) = card(U) – card(ЖÈМÈC) =

= 100 – (card(ЖÈМ) + card(C) – card((ЖÈМ)ÇC) =

= 100 – (card(Ж) + card(М) – card(ЖÇМ) + 42 card((ЖÇC)È(МÇC))) =  = 100 – (28 + 30 – 8 + 42 – (card(ЖÇC) + card(МÇC) –

– card(ЖÇМÇC)))= 100 – (92 – (10 +5 – 3)) = 100 – (92 – 12) = 20.

Теорема 3. Если card(A) = n, то card(b(A)) = 2ⁿ.

Доказательство. Рассмотрим множество

Еⁿ ={(v₁, v₂, ..., v _n): "v_kÎЕ},

где Е – множество, содержащее 2 элемента: 0 и 1. Из следствия теоремы 2 вытекает, что card (E ⁿ) = (card(E))ⁿ = 2ⁿ. Покажем, что множества Eⁿ и b(A) равномощны. Пусть множество A = {а₁, а₂, ..., а _n} и В некоторое подмножество A. Поставим в соответствие множеству В элемент (v₁, v₂, ..., v _n), полагая

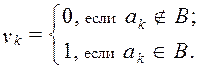
Несложно проверить, что данная функция является инъекцией и сюръекцией множества b(A) на множество Е. Таким образом, card(b(A)) = 2ⁿ.

Задачи.

1. Можно ли сказать, что если A = В, то A и В равномощны, и наоборот, если A и В равномощны, то A = В?

2. Доказать, что для любых трех конечных множества A, В, С справедливо равенство, называемое формулой включения и исключения:

card(AÈBÈC) = card(A) + card(B) + card(C) – card(AÇB) –

– card(AÇC) – card(BÇC) +card(AÇBÇC).