Технология проблемного обучения

Предмет «Алгебра и начала анализа».

Цели:

образовательные:

1. формирование понятия показательного уравнения;

2. формирование умения решения показательных уравнений.

развивающие:

1. развитие мышления учащихся, развитие математической речи;

2. развитие мотивационной сферы личности;

3. развитие исследовательских способностей.

воспитательные:

1. воспитание настойчивости при решение проблемы;

2. способствование формированию сотруднических отношений в классе при решение проблемы.

Тип урока: урок изучения нового материала.

Методы: объяснительно-иллюстративный, частично-поисковый, исследовательский.

Формы познавательной деятельности учащихся: фронтальная, индивидуальная.

Структура урока:

1этап. Организационный этап.

2этап. Актуализация опорных знаний и их коррекция.

3этап. Изучение новых знаний и способов деятельности.

4этап. Первичная проверка понимания изученного.

5этап. Подведение итогов занятия.

6этап. Информация о домашнем задании.

7этап. Рефлексия.

Ход урока:

1этап. Здравствуйте, садитесь.

2этап. Задание для устного обсуждения (записаны на доске): Как называются выражения: 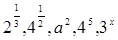. Какие еще два понятия связаны с этими выражениями.

3этап. Оглашается тема урока. Оглашаются цели урока:

· Узнать какие уравнения называются показательными.

· Научиться решать показательные уравнения.

Учащиеся записывают тему урока.

Раскрывается доска, на которой записаны уравнения:

(1)

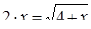
(2)

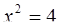
(3)

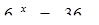
(4)

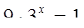
(5)

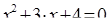
(6)

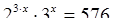
(7)

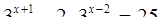
(8)

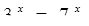
(9)

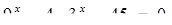
(10)

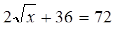
 Учащимся предлагается следующее задание:

Устно объедините эти уравнения в группы и попытайтесь объяснить, по какому признаку проведено распределение.

Ученики: Уравнения (1) и (10) можно объединить в одну группу, так как это иррациональные уравнения.

Уравнения (2) и (5) можно объединит в одну группу, так как это квадратные уравнения.

Уравнения (3), (4), (6), (8), (9) тоже можно объединить в одну группу, так как у этих уравнений есть общий признак: неизвестное у всех этих уравнений находится в показатели степени.

Учитель: Верно. Вы, наверное, уже догадались, как называются уравнения, входящие в последнюю группу.

Ученики: Показательные уравнения.

Учитель: Попробуйте дать определение показательным уравнениям. (Замечание: предварительно с учениками можно вспомнить определение иррациональных уравнений, а далее по аналогии дать определение показательным уравнениям).

Ученики: Показательные уравнения – это уравнения, в которых неизвестное содержится в показателе степени.

 Учитель: Запишите с доски в тетрадь только показательные уравнения. Я подчеркну показательные уравнения.

Далее учащимся предлагается некоторая порция теоретического материала.

Рассмотрим уравнения, следующего вида:

  , , , .

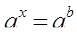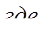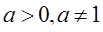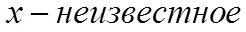Уравнения такого вида называются простейшими показательными уравнениями. Запишите это в тетрадь. Такие уравнения решаются с помощью свойства степени:

Степени с одинаковым основанием, а>0, а¹1 равны только тогда, когда равны их показатели.

Посмотрите на выписанные вами показательные уравнения. Какие из них являются простейшими уравнениями.

Ученики: Уравнение (3) 6  ^х = 36.

Учитель: Верно. Давайте его решим.

Учитель записывает решение уравнения на доске, ученики в тетради.

Учитель: Посмотрите на остальные показательные уравнения. Являются ли они простейшими?

Ученики: Нет.

Учитель: Как же мы будем их решать?

Итак, у нас возникла проблема: Как решать остальные показательные уравнения, которые не являются простейшими показательными уравнениями. Ваши предложения.

Возникает предположение (гипотеза): не простейшие показательные уравнения можно путем преобразований привести к уравнению вида 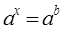, которое уже является простейшим, и которое мы умеем решать (формулируется учащимися, или учителем и учащимися, при затруднении последних).

(Замечание: эта гипотеза может возникнуть в результате решения уравнения ).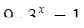

Далее, решаются все оставшиеся уравнения с использованием гипотезы, что и является в некотором роде ее практическим доказательством.

Закончить решение уравнений с доски можно общим выводом:  решение любого показательного уравнения сводится к решению простейшего показательного уравнения.

4этап. Предлагается решить уравнение: №210 (6).

Далее предлагается решить уравнение №211(2) самостоятельно, предварительно побеседовав с учащимися о способе решения. Через пять минут учитель просит одного из учащихся сказать получившийся у него ответ, другие учащиеся проверяют правильность своего ответа.

5этап. Итоги подводятся серией вопросов: Какие мы сегодня уравнения учились решать? Какие виды уравнений еще вы знаете? Какая основная идея используется при решении любого показательного уравнения?

6этап. Запишите домашнее задание: §12, №209(1,2), №210(3), 211(1,4). Учитель комментирует домашнее задание.

7этап. Учитель: Подумайте, все ли вы сегодня поняли на уроке и почему? Если что-то было не понятно, то почему? Все ли вы усилия приложили, чтобы понять новый материал?

На данные вопросы можно побеседовать с учащимися.

Приложение № 4.