Урок как целостная система исследовался Г. Д. Кирилловой, считающей, что более глубокое понимание урока возможно только в том случае, если его рассматривать как систему. Необходимость системного подхода к изучению и объяснению урока была осознана педагогами лишь в 70-е гг.
Дадим определение понятию система.
Система (от греч. systema – целое, составленное из частей; соединение), множество элементов, находящихся в отношениях и связях друг с другом, образующих определенную целостность, единство [4].
Дадим еще одно определение, более полно характеризующее понятие системы.
Система – определенная целостность, которая состоит из комплекса элементов, находящихся во взаимных связях и отношениях друг с другом. Система представляет собой единое целое и способна к самостоятельному функционированию, саморазвитию. Признаки системы: наличие системообразующего фактора, взаимодействие элементов, иерархия связей, единство, целостность [70].
Итак, для рассмотрения современного урока с позиции системного подхода необходимо, учитывая определение системы, выделить элементы, части урока. Исходя из анализа педагогической литературы, такими элементами урока считаются:
· содержание учебного материала;
· методы обучения;
· формы организации учебно-познавательной деятельности учащихся (формы обучения);
· субъекты урока (преподаватель и учащиеся).
Триединая цель урока является системообразующим фактором современного урока как целостной системы. Интегративный результат «жизни» урока как системы принято называть реальным результатом урока. Так как функция системы считается интегративным результатом функционирования образующих ее компонентов, то реализация функции урока и являются результатом урока.
Рассматривают и такое понятие как подсистема урока. Подсистемой считается такая часть системы, которая состоит из того же комплекса элементов, что и сама система.
В качестве подсистемы урока рассматривают этап урока. Он является относительно завершенным отрезком урока, представляющий собой систему взаимосвязанных элементов: ·содержания; ·методов; ·форм организации учебно-познавательной деятельности учащихся; ·субъектов этапа.
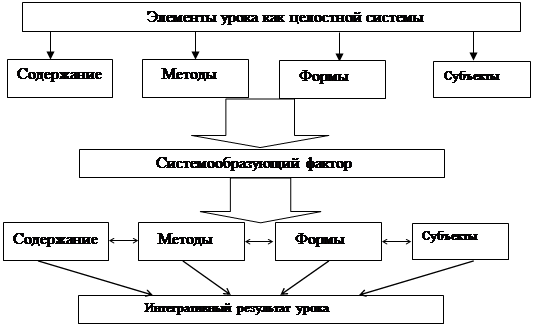
Схема 3. Современный урок как целостная система.
Системообразующим фактором этапа как подсистемы урока являются образовательные задачи этапа. Образовательная задача – это запрограммированный результат конкретного этапа урока. Она объединяет все элементы этапа в единое относительно целостное образование. Результатом функционирования этапа как подсистемы является реальный результат этапа. Он выражается, прежде всего, в тех знаниях, умениях и навыках, которые приобрели учащиеся. Трудно предвидеть на этапе изменения в ценностных отношениях учащихся и их развитии.
Дадим краткую характеристику рассмотренных элементов.
Содержание учебного материала составляет содержательную основу каждого этапа учебного занятия. Сюда входят не только теоретические сведения, правила, теоремы, законы, но и задачи, упражнения, вопросы учителя, отражающие последовательность умственных действий ученика. То есть все то, что должен усвоить ученик и что способствует этому усвоению.
Метод обучения, система последовательных взаимосвязанных действий учителя и учащихся, обеспечивающих усвоение содержания образования [63].
Метод обучения – путь, способ взаимодействия учителя и учащихся на основе комплексной последовательности приемов преподавания и учения, направленный при руководящей роли учителя на достижение целей обучения [70].
С понятием «метод обучения» связано и такое понятие как «прием обучения».
Прием обучения, конкретная операция взаимодействия учителя и учащихся в процессе реализации метода обучения [63].
Приведем одну из классификаций методов обучения. Так в работе Ю. А. Конаржевского «Анализ урока» предложена классификация В. И. Бондаря, строящаяся на основе четырех классификационных признаков:
1. Группа методов по характеру источников информации: словесные, наглядные, практические.
2. Группа методов по уровню познавательной самодеятельности учащихся: объяснительно-иллюстративные, репродуктивные, проблемные, частично-поисковые, исследовательские.
3. Группа методов по их дидактическим функциям: контроль, обобщение, осознание, восприятие, применение.
4. Группа логических методов обучения: традуктивные, индуктивные, дедуктивные.
В настоящее время в учебно-воспитательном процессе школы используются методы, направленные на развитие мышления учащихся. Самый распространенный метод – это эвристическая беседа, сущность которой состоит в том, что учитель не сообщает учащимся готовых знаний, а умело поставленными вопросами заставляет учеников на основе уже имеющихся знаний, личного жизненного опыта приходить к новым понятиям и выводам. Метод проблемного обучения, исследовательский метод, эвристические разминки, беседы как активные методы получили широкое распространение в современной школе. Одним из новейших методов обучения применяемых в школе в последнее время является учебный диалог.
В современной дидактике различают понятие «форма организации обучения» (урок, экскурсия и т. д.) и «форма обучения» или по-другому, что более употребляют в литературе последних лет, «форма организации познавательной деятельности учащихся». К формам организации учебно-познавательной деятельности учащихся относится система средств, с помощью которых учитель добивается включения каждого ученика в активную целенаправленную учебно-познавательную деятельность [32].
Различают следующие формы познавательной деятельности учащихся: ·индивидуальная форма; · фронтальная форма познавательной деятельности; · групповая форма организации познавательной деятельности; · коллективная форма познавательной деятельности учащихся.
Не нужно забывать, что методы обучения и формы обучения направлены не только на обогащение учащихся знаниями и умениями, но и важна их роль как средство общего развития и воспитания учащихся.
Итак, прежде всего данный параграф предназначался для общей характеристики понятия современного урока, для описания основных понятий тесно связанных с понятием урока (без которых полно описать современный урок было бы не возможно). Это такие понятия как структура урока, типология урока, методы обучения, содержание обучения, формы познавательной деятельности учащихся.
Попытаемся теперь выделить основные требования к современному уроку.
Требования к современному уроку.
Остановимся на требованиях к уроку как организационной форме обучения. В педагогической литературе число таких требований колеблется от 6 до 18 и более. В дидактике есть и попытки классификации требований к уроку.
Для формулировки наиболее полной, корректной и «современной» системы требований к современному уроку рассмотрим требования к уроку различных педагогов.
2.1. Различные системы требований к уроку.
Система требований Н. А. Сорокина.
Н. А. Сорокин приводит важнейшие из дидактических требований, которыми должен обладать урок: 1) четкость определения учебных задач урока, выделение из них главной и второстепенной; 2) единство образовательных и воспитательных задач; 3) определение оптимального содержания и отбор учебного материала урока в соответствии с его задачами и возможностями, определяемыми уровнем подготовки учащихся, обеспечение урока необходимым оборудованием; 4) выбор наиболее рациональных методов и приемов обучения, использование их с учетом дидактических задач урока и особенностей учебного материала на каждом его этапе, обеспечение познавательной активности учащихся, сочетание коллективной работы с самостоятельностью каждого ученика; 5) связь содержания урока с жизнью, с практикой, с ранее пройденным и подлежащим дальнейшему изучению материалом; 6) организационная четкость урока.
Приведем систему требований к уроку В. А. Онищука.
В. А. Онищук выделяет общие требования к уроку, вытекающие из задач, которые общество ставит перед школой. Кратко их можно сформулировать так: 1) вооружать учащихся сознательными, глубокими и прочными знаниями; 2) формировать у учащихся прочные навыки и умения; 3) повышать воспитательный эффект обучения на уроке; 4) осуществлять всестороннее развитие учащихся; 5) формировать у учащихся самостоятельность, творческую активность, инициативу как устойчивые качества личности, умения творчески решать задачи; 6) вырабатывать у школьников умения самостоятельно учиться, приобретать и углублять или пополнять знания, работать с книгой, овладевать навыками и умениями и творчески применять их на практике; 7) формировать у детей положительные мотивы учебной деятельности, познавательный интерес, желания учиться, потребность в расширении и приобретении знаний, положительное отношение к учению; 8) воспитывать у учащихся трудолюбие.
Общие требования уточняются и конкретизируются в требованиях, которые В. А. Онищук делит на четыре группы: воспитательные, дидактические, психологические, гигиенические. Условность этого деления автор видит в том, что в реальной действительности все эти требования тесно связаны между собой, взаимопроникают друг в друга. Приведем дидактические требования к уроку:
- организационная четкость проведения урока, обеспечивающаяся правильной постановкой образовательной и воспитательной целей и конкретных задач урока;
- основные требования к педагогическому руководству учебно-воспитательной деятельностью школьников заключаются в следующем: обеспечивать познавательную активность детей на уроке, рационально сочетать разнообразные методы обучения с проблемными;
- постоянно соблюдать и творчески реализовать на уроке все дидактические принципы в их единстве и взаимосвязи;
- постоянно осуществлять связь данного урока с предыдущим на основе воспроизведения учащимися и коррекции учителем опорных знаний и практического опыта, обобщения и систематизации знаний – понятий, усвоенных на данном уроке, с изученными прежде;
- постоянно привлекать учащихся к активной познавательной деятельности, к самостоятельному приобретению знаний; организовывать закрепление знаний не только посредством их воспроизведения, но и на основе выполнения различных познавательных заданий.
Психологические требования к уроку:
- учитель должен всесторонне изучать и учитывать на уроке психологические особенности каждого учащегося: его мышления, памяти, внимания, воображения, воли, эмоций и т. п.;
- учитель должен отличаться самообладанием и самоконтролем, чтобы преодолевать отрицательное психическое состояние на уроке;
- умелое руководство мотивами учения школьников.
Гигиенические требования к уроку:
- соблюдение в классе гигиенических требований;
- избегать однообразия в учебной работе, с целью предупреждения умственного переутомления.
Система требований к уроку Н. Г. Дайри.
Н. Г. Дайри приводит вариант требований к уроку изучения нового материала и комбинированному: 1) усвоение основного содержания урока на самом уроке; 2) полноценность содержания урока; 3) полноценность педагогического замысла (правильное определение значения данного урока в системе образования и отсюда его главного вклада в формирование знаний, в нравственное и эстетическое воспитание; умелое использование закономерностей образовательного и воспитательного процесса для реализации возможностей урока; реалистическое определение нагрузки учащихся); 4) постановка перед учащимися цели их деятельности и мотивация учения: что должны они усвоить на уроке, каким умениям научиться, в какой мере; 5) использование различных видов мотивации, соответствующих содержанию урока, характеру предстоящей познавательной деятельности и возрасту учащихся; 6) реализация замысла на основе высокой активности всех познавательных процессов, ведущей роли самостоятельной деятельности учащихся и ее рационального сочетания с усвоением готовых знаний, целостность педагогического воздействия; 7) использование различных видов самостоятельной работы как доминанты, улучшающей усвоение готовых знаний; 8) правильный выбор и использование различных методов обучения, приемов учебной работы; 9) ориентация на обучение всех учащихся, гибкость методики урока: разработка его вариантов, реагирование педагога на вопросы учащихся, возникшие неожиданности, трудности, умение по ходу урока перестроить изложение; умение соотносить методику с возрастом учащихся, зоной их ближайшего развития; 10) воспитание трудолюбия, прилежания, интереса к предмету, умения самостоятельно расширять, углублять знания.
Система требований к уроку Ю. Б. Зотова.
Ю. Б. Зотов делит требования к уроку на четыре группы.
Требования к структуре говорят о необходимости
§ правильно определить дидактические и воспитательные цели урока и его значение в системе уроков по теме (весь материал урока расчленяется на законченные в смысловом отношении части, для каждой части определяется конкретная цель, и продумываются оптимальные средства ее достижения);
§ определить тип урока, продумать и обосновать его структуру (все части урока должны быть взаимосвязаны друг с другом);
§ связать данный урок с предыдущими и последующими уроками;
§ отобрать и применить оптимальное сочетание методов изучения нового материала;
§ обеспечить систематический и разнообразный обучающий контроль знаний учащихся;
§ продумать систему повторения и закрепления изученного материала;
§ найти оптимальное место домашнему заданию.
Требования к подготовке и организации урока сводятся в основном к следующим:
§ обеспечить на уроке охрану здоровья школьников (соблюдать технику безопасности, гигиену труда, чистоту помещения);
§ начинать подготовку к каждому конкретному уроку с планирования системы уроков по данной теме;
§ своевременно подготовить к каждому уроку демонстрационный и дидактический материал;
§ обеспечить разнообразие типов уроков в системе уроков по данной теме;
§ создать возможность для учащихся часть знаний на уроке получать самостоятельно под руководством учителя.
Требования к содержанию урока и процессу учения:
§ урок должен быть воспитывающим;
§ выполнение требований, вытекающих из основных дидактических принципов;
§ на уроке следует воспитывать любовь к природе;
§ процесс поиска истины должен быть строго обоснованным, умозаключения учащихся и учителя доказательными, лабораторные и практические работы должны включать элементы творческого поиска;
§ в процессе учения надо воспитывать аккуратность, терпеливость, упорство в достижении цели, умение вести себя в коллективе и т. д.
Требования к технике проведения урока:
§ урок должен быть эмоциональным, вызывать интерес к учению, воспитывать потребность в знаниях;
§ темп и ритм урока должен быть оптимальным, действия учителя и учеников завершенными;
§ необходим полный контакт во взаимодействии учителя и учащихся на уроке;
§ создать атмосферу доброжелательности и активного творческого труда;
§ менять по возможности виды деятельности учащихся, оптимально сочетать разнообразные методы обучения;
§ управлять учебным процессом на уроке, большую часть урока активно работают учащиеся.
Система требований к уроку Н. М. Яковлева.
Н. М. Яковлев приводит 11 требований к уроку, суть которых затем последовательно раскрывает. Приведем лишь сами требования: 1) отчетливая целенаправленность урока; 2) достаточное организационное и материальное обеспечение урока; 3) оптимальный психологический режим урока; 4) оптимальный темп и ритм работы на уроке; 5) систематическая последовательность и преемственность учебных операций; 6) завершенность операций; 7) экономия времени на уроке; 8) непрерывный контроль и самоконтроль; 9) восстановление делового равновесия при его нарушении; 10) закрепление и «отделка» знаний и умений; 11) непрерывное совершенствование учебного процесса (обобщающее требование).
Система требований к уроку М. И. Махмутова.
В своей книге «Современный урок» М. И. Махмутов наиболее строго и полно подходит к требованиям к уроку. Автор считает, что в требованиях к уроку - каким он должен быть – часто повторяются те же мысли, которые заложены в дидактических принципах, в условиях организации учебного процесса и правилах обучения. Исходя из этого, М. И. Махмутов определяет следующие понятия: условия организации урока, правила его организации, требования к уроку, и пытается определить каково соотношение этих понятий.
Под условиями понимается наличие факторов, без которых невозможна нормальная организация урока. По мнению М. И. Махмутова анализ учебного процесса позволяет выделить две группы условий: социально-педагогические и психолого-дидактические.
В группе социально-педагогических условий можно отметить наличие четырех наиболее важных условий: • наличие квалифицированного, творчески работающего учителя; • наличие коллектива учащихся с правильно сформированной ценностной ориентацией; • наличие необходимых средств обучения; • наличие благоприятного психологического климата, доверительных отношений между учащимися и учителем, основанных на взаимном уважении.
В группе психолого-дидактических условий можно указать следующие условия: • уровень обученности учащихся, соответствующий программным требованиям; • наличие обязательного минимума сформированности мотивов учения и труда; • соблюдение дидактических принципов и правил организации учебно-воспитательного процесса;
Всю совокупность правил к организации урока М. И. Махмутовым делится на правила, вытекающие из дидактических принципов (основных правил) и специальные правила организации урока, которые основаны на логике процесса обучения, принципах обучения и закономерностях преподавания. Эта обязательность соблюдения правил и воспринимается как совокупность требований к уроку.
Специальные правила организации урока:
§ определить общую дидактическую цель урока, включающую образовательную, воспитательную и развивающую составляющие;
§ подготовить содержание учебного материала, определив его объем и сложность в соответствии с поставленной целью и возможностями учащихся;
§ определить дидактические задачи урока, последовательное решение которых приведет к достижению всех целей;
§ выбрать наиболее эффективное сочетание методов и приемов обучения в соответствии с поставленными целями, содержанием учебного материала, уровнем обученности учащихся и дидактическими задачами;
§ определить структуру урока, соответствующую целям и задачам, содержанию и методам обучения;
§ поставленные дидактические задачи стремиться решать на самом уроке и не переносить их на домашнюю работу.
2.2. Конструирование современной системы требований к современному уроку.
Пути повышения эффективности обучения ищут педагоги всех стран мира. Одним из путей повышения эффективности обучения является выполнение требований к уроку.
Итак, какие же требования предъявляются к современному уроку?!
Нужно отметить, что наряду с традиционными требованиями, рассмотренными выше, важность которых никем не опровергается, появляются и новые требования к уроку. Эти новые требования:
· реализуют достижения современной дидактики, психологии, педагогики;
· появляются в результате качественного изменения образования на современном этапе:
Ø На смену учебно-дисциплинарной модели образования приходит личностно-ориентированная модель, которая рассматривает учащихся как полноправных партнеров в условиях сотрудничества, характеризуется усилением внимания к ученику, к его саморазвитию и самопознанию, обращенностью ученика к окружающему миру и к себе, к воспитанию умения искать и находить свое место в жизни.
Ø В современном обществе актуальной является проблема гуманизации и гуманитаризации образования. Слово «гуманизм» происходит от латинского «humanus» - человечный. Гуманизация образования предпологает «очеловечивание» знаний, т.е. такую организацию учебного процесса, при котором знания имели бы для ученика личностный смысл. Важными условиями гуманизации образования являются усиление мотивации и дифференциации обучения. Слово «гуманитарный» происходит от латинского «humanitas», что означает духовная культура. Смысл гуманитаризации образования заключается в приобщении ученика к духовной культуре, творческой деятельности, методологии открытия нового.
В результате обучение, находящееся в прямой зависимости от образования, реализует идеи личностно-ориентированного подхода в образовании возникновением различных личностно-ориентированных технологий обучения. Это, например такие технологии, как: • адаптивная система обучения, • технология дифференцированного обучения, • технология модульного обучения, • информационные технологии обучения (компьютерные технологии), • технология полного усвоения знаний, • технология коллективного способа обучения, • технология интегрированного урока.
Это далеко не весь перечень существующих на сегодняшний день педагогических технологий.
Вообще, педагогическая технология – это совокупность средств и методов воспроизведения теоретически обоснованных процессов обучения и воспитания, позволяющих успешно реализовывать поставленные образовательные цели [63].
Или более конкретно:
Педагогическая технология – это направление, которое ставит целью повысить эффективность образовательного процесса, гарантировать достижения учащимися запланированных результатов обучения [41].
Технологию обучения понимают как построение системы целей (от общих к конкретным) для достижения определенного результата развития ученика с высокой вариативностью использования методов, приемов, средств и форм организации обучения [41].
Итак, анализируя традиционные требования к уроку, учитывая ключевые направления развития образования, попытаемся сформулировать современную систему требований к современному уроку.
Каждый урок направляется на достижение триединой цели: обучить, воспитать, развить. С учетом этого конкретизируем всевозможные требования к уроку в три группы: образовательные требования, воспитательные и развивающие требования.
Образовательные требования.
1. Целенаправленность урока.
Требования к целям и к постановке целей урока уже были рассмотрены выше (см. стр.10).
2. Рационализация и дифференциация информационного наполнения урока:
§ научность содержания;
§ дифференциация содержания (по степени сложности, глубине, объему усвоения и видам помощи);
§ структурирование содержания (в содержании предусмотрены задания в соответствии со всеми целями урока и этапами усвоения; структурное основание блоков знаний идет с опорой на модели, схемы, таблицы совместно с учащимися на всех этапах урока).
3. Обоснованный выбор средств, методов и приемов, ориентированных на обучение, развивающее личность:
§ выбранные методы соответствуют целям урока, оптимально соотносятся с содержанием урока (широкий арсенал, оптимальное сочетание) ;
§ оптимальное сочетание репродуктивных (объяснительно-иллюстративный, репродуктивный) и продуктивных методов обучения (проблемный, частично-поисковые, исследовательский);
§ оптимальное сочетание методов работы под управлением учителя и самостоятельной работы учащихся;
§ диалогичность методов, создание условий для того, чтобы каждый ученик мог выразить собственную точку зрения, соотнести ее с позицией других;
§ ориентация методов на самостоятельность и активность учащихся в процессе обучения, частичную передачу функции организации и управления от учителя ученикам, сотворчество учащихся и преподавателя (деятельностный подход к обучению).
4. Разнообразие форм организации учебной деятельности учащихся:
§ оптимальное соотношение форм организации учебной деятельности учащихся с целями и содержанием урока;
§ преимущественное использование таких форм организации учебной деятельности учащихся, которые обеспечивают сотрудничество, совместную деятельность учащихся.
5. Вариативный подход к формированию структуры урока:
§ использование современных технологий обучения;
§ рациональное использование уроков традиционных и нетрадиционных форм;
§ творческая основа конструирования структуры урока.
Также структура урока должна соответствовать цели урока и логике усвоения знаний (восприятие, осмысление, запоминание, применение, обобщение).
6. Реализация на уроке в оптимальном соотношении всех дидактических принципов и правил из них вытекающих.
В настоящее время выделяют следующие дидактические принципы обучения: воспитывающего и развивающего обучения; научности; связи теории с практикой, обучения с жизнью; наглядности; доступности; систематичности и последовательности; самостоятельности и активности учащихся в процессе обучения; сознательности и прочности усвоения знаний и умений; целенаправленности и мотивации обучения; индивидуального и дифференцированного подхода к обучению учащихся.
Из дидактических принципов вытекают правила обучения, которые подчиняются принципу, конкретизируют его, определяют характер отдельных методических приемов, используемых преподавателем, и ведут к реализации данного принципа. Принципы отражают сущность процесса обучения, а правила – его отдельные стороны.
Воспитательные требования.
«Сорок пять минут урока – одно из удивительных педагогических явлений, когда многообразные влияния сливаются в единый комплекс. И, сливаясь, они образуют такой огромной силы фактор развития ребенка, становления его как личности… воспитание в школе надо строить, начиная с урока, этого важнейшего фактора развития личности вообще и нравственного развития в частности» ([81]).
Реализация воспитательных целей, воспитательных требований урока – один из важнейших элементов современного обучения. В некоторой мере это результат перехода к личностно-ориентированному образованию. Ведь воспитательная среда на уроке позволяет раскрыть потенциал человека, реализовать ему свои сущностные принципы.
Урок обладает возможностями влиять на становление очень многих качеств личности учащихся. И эти возможности необходимо использовать в полной мере.
Итак, «урок должен быть воспитывающим» (Ю. Б. Зотов, одно из требований к уроку).
Что под этим подразумевается.
1 . Выявление и использование на уроке воспитательных возможностей:
§ содержания учебного материала, методов обучения, форм организации познавательной деятельности в их взаимодействии;
§ системы отношений, складывающейся на уроке.
Так Н. Е. Щуркова считает, что воспитывающее обучение – это такое обучение, в процессе которого организуется целенаправленное формирование запланированных педагогом отношений учащихся к различным явлениям окружающей жизни, с которыми ученик сталкивается на уроке.
2. Четкая постановка воспитательных целей и реализация этих целей через систему воспитательных задач.
Постановка воспитательных целей урока осуществляется в русле целостного подхода к процессу формирования базовой культуры личности, основными направлениями которой являются духовно-нравственная, экологическая, трудовая, интеллектуальная, эстетическая культура.
Достижение почти всех воспитательных целей невозможно на одном уроке и поэтому необходимо из урока в урок, имея в виду одну воспитательную цель, ставить различные воспитательные задачи эту цель реализующие.
3. Организация сотрудничества в процессе урока.
Сотрудничество – определенные взаимоотношения между участниками совместной деятельности, в которой они равноправны, доверяют, помогают и проявляют терпимость друг к другу, окружающим людям ([70]).
Т. В. Машарова считает, что важнейшими признаками сотрудничества являются [40]:
1. Осознание общей цели, которая мобилизует учителя и учащихся; стремление к ее достижению, взаимная заинтересованность в этом; положительная мотивация деятельности.
2. Высокая организация совместного учебного труда участников учебного процесса, их общие усилия; взаимная ответственность за результаты деятельности.
3. Активно-положительный, гуманистический стиль взаимоотношений учащихся и взрослых при решении учебных задач; взаимное доверие, доброжелательность, взаимопомощь при затруднениях и учебных неудачах. Этот стиль несовместим с авторитарным отчуждением между учащимися и взрослыми, преобладанием прав у взрослых и обязанностей школьников.
4. Методика обучения, стимулирующая интересы учащихся, их самостоятельность, практическую и интеллектуальную инициативу, творчество. Она исключает принуждение, монополию педагогов на интерпретацию знаний, пассивное восприятие учащимися готовой информации.
5. Взаимодействие учащихся друг с другом, их деловое общение и коллективная ответственность за результат общего труда.
6. Сотрудничество учащихся с другими объектами социальной среды в процессе выполнения учебных заданий.
Выполнимость воспитательных требований на уроке, достижение воспитательных целей определяется, как правило, в процессе наблюдения за уровнем гуманистических отношений, которые складываются между одноклассниками и между школьниками и учителем.
Вообще, «воспитание начинается с нравственности» [81]. Поэтому главная цель воспитания: развитие нравственного сознания, нравственного самосознания и нравственных мотивов. Ожидаемый результат: нравственная позиция, нравственное поведение участников педагогического процесса.
Развивающие требования.
1. Развитие умений творческого характера (формирование опыта творческой деятельности).
2. Развитие речи, развитие мышления, развитие памяти, развитие сенсорной сферы, развитие двигательной сферы, развитие познавательного интереса и любознательности.
3. Формирование и развитие у учащихся системы не только специальных предметных, но и общеучебных умений и навыков, которые служат основой для реализации любой деятельности (развитие умений учебно-познавательной деятельности).
4. Изучение и учет уровня развития и психологических особенностей учащихся, проектирование «зоны ближайшего развития».
5. Проведение учебных занятий на «опережающем» уровне, стимулирование наступления новых качественных изменений в развитии.
6. Развитие интеллектуальной, волевой, эмоциональной, мотивационной сфер личности.
Сделаем некоторые выводы. Целью данного параграфа было конструирование системы требований к современному уроку. Система требований к уроку строилась на основе анализа требований к уроку различных педагогов, а также при построении системы требований учитывались ключевые направления развития образования.
В заключении хочется еще немного поговорить об общении, о педагогическом общении.
« Опыт педагогической деятельности показывает, что недостаточно только знания учителем основ наук и методики учебно-воспитательной работы. Ведь все его знания и практические умения могут передаваться учащимся только через систему живого и непосредственного общения с ними» ([25]).
Выше мы сконструировали современную систему требований к современному уроку. Эффективная реализация большинства требований возможна только посредством педагогического общения.
Педагогическое общение – это профессиональное общение преподавателя с учащимися на уроке и вне его (в процессе обучения и воспитания), имеющее определенные педагогические функции и направленное (если оно полноценно и оптимально) на создание благоприятного психологического климата, а также на другого рода психологическую оптимизацию учебной деятельности и отношений между педагогом и учащимися внутри ученического коллектива ([22]).
Понятие общения тесно связано с понятием сотрудничества. Вообще, общение возникает из потребности сотрудничества ([70]). Как «работает» общение при реализации целей урока (обучающей, воспитывающей и развивающей) описано в книге Кан-Калика В.А. «Учителю о педагогическом общении».
Итак, система требований к современному уроку сконструирована. Посмотрим теперь, как реализуются эти требования на уроках математики.
Глава 2. Реализация требований к современному уроку математики .
§1. Реализация требований к современному уроку в опыте работы учителей математики.
Поговорим немного о современном математическом образовании.
Математика на протяжении всей истории человечества являлась составной частью человеческой культуры, ключом к познанию окружающего мира, базой научно-технического прогресса. Математическое образование является неотъемлемой частью гуманитарного образования в широком понимании этого слова, существенным элементом формирования личности.
Математика есть часть общего образования. Ныне ни одна область человеческой деятельности не может обходиться без математики – как без конкретных математических знаний, так и интеллектуальных качеств, развивающихся в ходе овладения этим учебным предметом. Школьное математическое образование способствует: овладению конкретными знаниями, необходимыми для ориентации в современном мире; приобретению навыков логического и алгоритмического мышления; развитию воображения и интуиции; формированию мировоззрения; формированию нравственных черт; воспитанию способности к эстетическому восприятию мира; обогащение запаса историко-научных знаний.
Огромно значение математического образования в воспитании всесторонне развитой личности. Это еще раз убеждает о необходимости проведения уроков математики с учетом общих требований к современному уроку, выполнение которых повышает эффективность уроков математики, а значит и качество математического образования.
Итак, как на сегодняшний день реализуются требования к современному уроку в опыте работы учителей математики.
В 30-х годах прошлого столетия в связи с восстановлением урока в качестве основной организационной формы учебной работы в школе, усилия методистов стали направляться на разработку требований к уроку математики, выявление особенностей построения отдельных его этапов, совершенствование методов и приемов обучения. В этот период в теории и практике урока математики начинают использоваться достижения педагогической психологии (концепции программированного обучения, алгоритмизации обучения, проблемного обучения и др.), распространяется опыт работы, как учителей целых регионов, так и отдельных учителей. К концу данного периода назрели проблемы дифференциации и индивидуализации в обучении математике.
В методике преподавания математики проблемы дифференциации, личностной ориентации в обучении и развитии интенсивно стали исследоваться с середины 80-х годов 20 века (М. Б. Волович, А. Г. Мордкович, Г. И. Саранцев, Л. М. Фридман и др.). Расширились возможности реализации в практике обучения результатов данных исследований, равно как и совершенствование процесса обучения математике в целом, с предоставлением общеобразовательным учреждениям самостоятельности в выборе форм обучения в пределах, определенных Законом Российской Федерации «Об образовании».
В этих условиях стал более востребованным и опыт работы учителей-новаторов А. А. Окунева, В. И. Рыжика, Р. Г. Хазанкина, Н. И. Зильберберга и др. В их работах освещались отдельные вопросы подготовки и проведения современного урока математики.
В 1997 г. завершается крупное исследование проблем современного урока математики С. Г. Манвеловым, результаты которого составили основу его докторской диссертации, а также вышедшей в 2002 году работы «Конструирование современного урока математики».
В итоге на сегодняшний день в практике обучения математики накоплен богатейший опыт проведения уроков, частично отраженный в психолого-педагогической и методической литературе.
Постараемся выделить основные направления совершенствования урока математики. Они возникли в результате анализа статей теоретиков и практиков урока математики в газете «Математика» и журнале «Математика в школе», а также соответствующей литературы, и заключаются в соблюдении современных требований к уроку.
Основные направления совершенствования урока математики:
1. Современный урок математики характеризуется усилением функции управления процессом формирования новых знаний.
Под управлением процессом формирования новых знаний понимается такой способ формирования новых знаний, при котором учитель вместо изложения учебного материала в готовом виде подводит учащихся к «переоткрытию» теорем, их доказательств, к самостоятельному формулированию определений, к составлению задач и т. д. В результате учащиеся включаются в активную, творческую, познавательную деятельность.
В связи с этим на уроке математики часто используют активные методы формирования знаний: проблемного изложения, частично-поисковые (эвристические), исследовательские (см. стр. 22). Перечисленные методы (продуктивные) отличаются от репродуктивных (объяснительно-иллюстративный и репродуктивный), которые связаны с усвоением учеником готовых знаний и воспроизведения, известных ему способов деятельности, тем, что ученик добывает субъективно новые знания в результате творческой деятельности.
Проблемное изложение относят к промежуточной группе, ибо оно в равной мере предполагает как усвоение готовой информации, так и элементы творческой деятельности.
Но продуктивные методы имеют и ряд недостатков ([10]), поэтому нельзя полностью игнорировать репродуктивные методы как эффективные.
Т. М. Карелина в своей статье «Методы проблемного обучения» ([26]) приводит три конкретных примера создания проблемных ситуаций. Приведем один из них. Т. М. Карелина считает, что проблемная ситуация возникнет, если предложить ученикам выполнить какое-то действие, на первый взгляд не вызывающее затруднения. Так, перед изучением темы о сумме внутренних углов треугольника можно предложить такую задачу: «Построить треугольник по трем заданным углам:
1. ÐА=90°, ÐВ=60°, ÐС=45°;
2. ÐА=70°, ÐВ=30°, ÐС=50°;
3. ÐА=50°, ÐВ=60°, ÐС=70°.
Учащиеся, вооружившись линейкой и транспортиром, начинают строить треугольники. В первом случае, построив углы А и В и отложив угол в 45° от луча АС (или ВС, кому как нравится), ребята увидят, что вместо треугольника получается четырехугольник. Во втором случае независимо от того, какие первые два угла школьники выбирают для построения, всегда получается треугольник, третий угол которого либо больше, либо меньше заданного. И только в третьем случае выстраивается треугольник по трем заданным углам. По окончании уже можно выдвинуть предположение о сумме внутренних углов треугольника.
Приведем пример использование на уроках математики исследовательского метода. Так, в [43] предлагаются задачи и упражнения, включающие элементы исследования. Авторы считают, что простейшие исследования при решении задач следует предлагать уже с первых уроков алгебры и геометрии и даже на уроках математики в 4-5 классах. Например:
1. Существуют ли числа, обратные самим себе? Сколько таких чисел? Назовите их.
2. При каких значениях a и b верны: а) равенства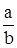 
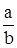=0; =1; 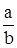=-1; б) неравенства 
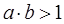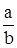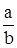; >1; <-1?
3. Установите вид треугольника (классифицируя по углам), если один из его внутренних углов: 1) равен сумме двух других; 2) больше ее; 3) меньше ее.
В последующих классах следует предлагать не только задачи с элементами исследований, но и задачи, включающие исследования в качестве обязательной составной части. Такие исследования необходимо включаются в решение многих геометрических задач на построение (как в планиметрии, так и в стереометрии), уравнений и неравенств (особенно тригонометрических, показательных и логарифмических с параметрами), также исследования находят широкое применение при изучении функций и их свойств в курсе алгебры и начал анализа.
2. Творческое отношение к структуре урока математики.
Стремление заинтересовать учащихся, разнообразить ход урока ведут к тому, что учителя включают в урок различные игровые методики. Как показывает педагогическая практика и анализ педагогической литературы, до недавнего времени игру использовали лишь на занятиях математического кружка, при проведении тематических вечеров и др., а возможности использования дидактической игры в учебном процессе недооценивались.
В настоящее время игру используют при организации начала урока, при изучении нового материала, при организации контроля, при окончании урока. Часто проводятся и игровые уроки.
Приведем пример использования элементов игры при организации контроля. Миненкова М. и Широкова О. [45] несколько лет подряд проводили комбинированные зачеты по теме «Решение уравнений и координатная плоскость», для которых разработали карточки с индивидуальными заданиями. Например, в каждой карточке для 6-ого класса содержится несколько уравнений и пара чисел, одно из которых – буква. Ученики решают уравнение, находят соответствующую координату и строят соответствующие точки. Последовательно решая ряд уравнений, выстраивая точки и соединяя их, они получают рисунок.
Приведем пример одной из карточек для 6-ого класса.
Решите уравнения, и построить по точкам соответствующий рисунок.
1. 6х+10=4х+12. (х;3)
2. 
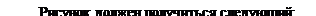7х+25=10х+6. (х;6)
3. 3у+16=8у-9. (5;у)
4. 0,4(6у-7)=0,5(3у+7). (5;у)
5. 4(3-х)=7(2х-5). (х;8)
6. 9,6-(2,6+х)=4. (х;8)
7. 1,7-0,6а=0,3-0,4а. (-6;а)
8. 17-4х=5-6х. (х;5)
9. 2,8-3,2х=-4,8-5,1х. (х;6)
10. 0,2(5х-2)=0,3(2х-1)-0,9. (х;3)
11. 5м+27=4м+21. (м;-4)
12. 4(1-0,5а)=-2(3+2а). (а;-7)
13. 3у-17=8у+18. (4;у)
14. 1-5(1,5+х)=6-7,5х. (х;-4)
15. 2у-1,5(у-1)=3. (1;у)
Очень важен творческий подход учителя к организации урока, в частности к организации начала урока. «Как правило, удачно выбранный вид деятельности учащихся вначале урока настраивает их на плодотворную работу на протяжении всех 45 минут»[50, с.18]. Новое начало урока позволяет избежать однообразия в построении занятия, обеспечивает интерес учащихся.
Как известно, предварительная содержательная работа на уроке направлена главным образом на подготовку учащихся к усвоению нового материала, применению имеющихся знаний, овладению определенными умениями. С этой целью Манвелов С. Г. предлагает использовать в начале урока: устный счет, математический диктант, игровые задания, задания на поиск закономерностей, на обнаружение типичных ошибок учащихся и их предупреждение, на выбор рациональных способов решения задач, комментированное чтение текста учебника и т.д. [37]. Окунев А. А. в своей работе «Спасибо за урок, дети!» предлагает 15 способов организации начала урока [50].
Рассмотрим пример организации начала урока в 6-ом классе, приведенный Манвеловым С. Г. в [37]. На уроке предстоит отработка умений складывать числа с разными знаками. Ранее уже было введено правило сложения чисел с разными знаками, поэтому перед учителем, прежде всего, стоит задача - выяснить, знают и понимают ли это правило учащиеся. Начать урок можно с решения следующего задания, подготовленного учителем.
Раскрывается одно из крыльев доски с таблицей
| 2 | -3 | 4 | -12 | |
| -5 | 3 | -2 | -8 | |
| -7 | 6 | -5 | 4 |
Учитель ставит задачу: найти правило, по которому составлена таблица, и вписать пропущенные числа. Выясняется, что числа верхней и нижней строк таблицы есть слагаемые, а средней – их сумма. Учитель предлагает обосновать это предположение, в ходе чего проверяет знания и понимание учащимися правила сложения двух чисел с разными знаками на конкретны примерах.
Необычность упражнения захватывает ребят, класс получает положительный заряд эмоций на весь оставшийся урок.
Традиционно, конец урока предвещает постановку домашнего задания. Однако способы окончания урока также полезно разнообразить: ∙ путем подведения итогов; ∙ ознакомления учащихся с обобщающими выводами и идеями; ∙ привлечения исторических сведений; ∙ выполнения игровых упражнений; ∙ решения головоломок, кроссвордов, ребусов на математическую тему.
Конечно это неполный список. Этот список может пополниться в результате вашего творчества!!!
Третье направление совершенствования урока математики.
3. Развитие технологического подхода к обучению математике.
К сожалению, в нашей педагогической, и особенно методической литературе, мало уделено внимания данной теме (именно использованию педагогических технологий на уроках математики).
Отметим, основные известные сегодня, частно-педагогические технологии обучения математике, которые на методическом уровне решают проблему конструирования процесса обучения, направленного на достижение запланированных результатов [17]:
1. Технология «Укрупнения дидактических единиц – УДЕ» (П. Эрдниев).
2. Технология, направленная на формирование общих подходов к организации усвоения вычислительных правил, определений и теорем через алгоритмизацию учебных действий учащихся (М. Волович), реализует теорию поэтапного формирования умственных действий П. Гальперина.
3. Технология обучения математики на основе решения задач (Р. Хазанкин).
Эта технология основана на следующих концептуальных положениях: 1) личностный подход, педагогика успеха, педагогика сотрудничества; 2) обучать математике = обучать решению задач; 3) обучать решению задач = обучать умениям типизации + умение решать типовые задачи; 4) индивидуализация обучения «трудных» и «одаренных»; 5) органическая связь индивидуальной и коллективной деятельности; 6) управление общением старших и младших школьников; 7) сочетание урочной и внеурочной работы.
4. Технология на основе системы эффективных уроков (А. Окунев).
5. Парковая технология обучения математике (А. Гольдин).
6. Технология мастерских построения знаний по математике (А. Окунев).
Применяются на уроках математики и различные личностно-ориентированные технологии обучения: технология дифференцированного обучения, технология модульного обучения, технология коллективного способа обучения, технология интегрированного урока.
Рассмотрим, для примера, более подробно технологию интегрированного урока. Цели интегрированных курсов – формирование целостного и гармоничного понимания и восприятия мира. Так, интересен опыт проведения интегрированного преподавания информатики и спецкурсов по математике Брейтигама Э. К. и Тевса Д. П. В статье [6] они приводят схему проведения интегрированных уроков, посвященных выполнению творческого задания по исследованию функции и построению ее графика. Авторы статьи предлагают провести 6 уроков. На совместном вводном уроке преподаватели информатики и спецкурса по алгебре и началам анализа определяют цель, план, этапы выполнения задания. Каждому ученику предлагается свое задание: устанавливаются сроки и требования к выполнению и защите творческого задания. На этом же уроке проводится первичная консультация по индивидуальным заданиям. Математическая составляющая этого урока включает разбор схемы исследования функции, работу с параметром. Составляющая по информатике включает построение алгоритма для решения задачи, схему реализации алгоритма с помощью языка программирования. Второй и третий уроки посвящены выполнению учащимися творческих индивидуальных заданий с консультациями преподавателей математики и информатики. Пятый и шестой уроки итоговые. Они строятся по схеме: индивидуальный отчет по заданию преподавателю, ведущему спецкурс по алгебре и началам анализа, после успешной защиты учащиеся отчитываются по этому же заданию преподавателю информатики. Также в статье приводятся цели работы с точки зрения математики и информатики, пример творческого задания.
4. Развитие способностей к математическому творчеству.
Развитие творческих способностей – это необходимый элемент современного урока математики. Воспитанию стремления к творчеству следует уделять пристальное внимание на всех этапах обучения. Каждый предмет школьного курса способен внести свою долю воздействия на творческий облик учащегося. Математика представляет для этого исключительные возможности.
Способности к математическому творчеству, и конечно творчеству вообще, развиваются в результате:
ü поиска решения нестандартных задач;
ü решения задач и упражнений, включающих элементы исследования;
ü решения задач на доказательство;
ü решения задач и упражнений в отыскании ошибок;
ü решения занимательных задач;
ü в отыскании различных вариантов решения одной задачи и выбора лучшего из них;
ü при решении задач, в которых применяются сведения из всех математических дисциплин (комбинированных задач);
ü при решении синтетических задач.
Важно и то, что от степени творческой активности учащихся зависит эффективность учебной деятельности по развитию мышления.
Подробнее о развитии способностей к математическому творчеству можно найти в статье Канина Е.С. «Некоторые вопросы психологии обучения решению математических задач» ([24]).
Итак, основные идеи современного урока, требования к современному уроку на уроке математики в опыте работы учителей находят свое отражение.
§2. Реализация требований к современному уроку в личном опыте преподавания математики.
Подготовка к проведению эксперимента.
Мною была проведена опытно-экспериментальная работа, целью которой было: выяснить повышает ли качество математического обучения соблюдение современных требований к современному уроку.
Эксперимент проводился в школе № 27 г. Кирова, в 10 “б” физико-математическом классе. Обучение в данном классе велось по учебнику Алимова М. А. «Алгебра и начала анализа 10-11».
Для достижения цели опытно-экспериментальной работы было проведено диагностирование обученности учащихся класса. Диагностирование обученности – это контроль и оценка знаний и умений обучаемых.
Приведем методику определения уровня обученности по П.И. Третьякову [74].
Обученность – это уровень реально усвоенных знаний, умений и навыков.
Существует пять уровней обученности.
Первый уровень обученности – различение. Он характеризуется тем, что ученик может отличить объект, процесс по наиболее существенным признакам от их аналогов.
Второй уровень обученности – запоминание. При этой степени обученности ученик может пересказать содержание текста, правила, положения, теоретические утверждения, но это не является доказательством его понимания, т. е. это только воспроизведение.
Третий уровень обученности – понимание. Ученик может находить существенные признаки и связи предметов и явлений, вычленять их из несущественных на основе анализа и синтеза; применять правила логического умозаключения, устанавливать сходства и различия.
Четвертый уровень обученности – умений и навыков.
Это наиболее высокий уровень обученности. Умения – закрепленные на практике способы применения знаний. Навык – умение, доведенное до автоматизма. Этот уровень обученности характеризуется умением применять на практике полученные теоретические знания, решать задачи с использованием усвоенных законов и правил.
Пятый уровень обученности – перенос знаний, умений и навыков в новую ситуацию. Обладающие этой степенью обученности умеют обобщать, применять полученные знания в новой ситуации.
Для определения обученности обычно используют самостоятельные работы, составленные в соответствии с уровнями обученности. Приведем ключевые слова для заданий самостоятельной работы по определению уровня обученности:
I уровень - различение: сравни, выбери, сопоставь, найди лишнее…
II уровень - воспроизведение: воспроизведи, нарисуй, напиши, перескажи товарищу…
III уровень – понимание: отчего, почему, зачем, в связи с чем, установи причинно-следственные связи, что может быть общего, выдели единичное, обобщи…
IV уровень – умений и навыков: выполни по образцу, по правилу, по формуле, перескажи, сопоставляя что-то с чем-то, какая закономерность, какие свойства…
V уровень – перенос: сочини, придумай, спроектируй, смоделируй, докажи, разыграй, выведи…
Диагностирование обученности включало в себя предварительный контроль, текущий контроль и итоговый контроль.
Предварительный контроль проводился с целью фиксации исходного уровня обученности (реально усвоенные знания, умения, навыки) и осуществлялся с помощью специально организованной самостоятельной работы по определению уровня обученности.
Текущий контроль необходим для диагностирования хода дидактического процесса, выявления динамики последнего; осуществлялся с помощью отслеживания итогов самостоятельных работ.
Итоговый контроль проводился с целью фиксации конечного уровня обученности и осуществлялся с помощью специально организованной самостоятельной работы по определению уровня обученности.
Сравнение исходного уровня обученности с конечным уровнем обученности позволяет судить об эффективности дидактического процесса и в итоге о повышении или понижении качества математического образования.
На момент проведения эксперимента класс изучил тему «Показательная функция, ее свойства и график». На эту тему и была организована самостоятельная работа диагностического характера, для определения исходного уровня обученности.
Предварительный контроль. Самостоятельная работа на тему «Показательная функция, ее свойства и график» (см. Приложение № 1).
Результаты предварительного контроля (см. Приложение № 2).
Дата: 2019-04-22, просмотров: 491.
