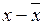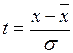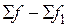Цель работы: ознакомление с расчетными приемами проверки соответствия данных выборочного наблюдения нормальному закону распределения
Ход работы
Этап 1. На основе данных о возрастном составе рабочих (лет): 18; 38; 28; 29; 26; 38; 34; 22; 28; 30; 22; 23; 35; 33; 27; 24; 30; 32; 28; 25; 29; 26; 31; 24; 29; 27; 32; 25; 29; 29 разработать интервальный ряд распределения и обработать исходные данные по следующей схеме (табл. 7):
Таблица 7
Интервальный ряд распределения
| Группы рабочих по возрасту (лет) x | Число рабочих f | Накопленная частота S |
| … | … | … |
| Итого |
Этап 2. Построить гистограмму распределения данных. Проверить нормальность распределения исследуемого факторного признака с помощью правила «трех сигм» (предварительно необходимо определить математическое ожидание m и среднее квадратическое отклонение s исследуемых данных).
Правило «трех сигм» определяет, что для нормально распределенной
случайной величины все рассеивание с точностью до долей процента укладывается на участке m ±3s. Это позволяет, зная s и m случайной величины, ориентировочно указать интервал ее практически возможных значений.
Правило трех сигм как способ оценки диапазона возможных значений случайной величины позволяет формировать интервал возможного изменения случайной величины [m-3 s; m+3 s] .
Результаты проверки на нормальность распределения представить в табличной форме (табл. 8).
Таблица 8
Проверка данных на соответствие нормальному закону распределения
| Интервалы значений признака | Число единиц, входящих в интервал | Удельный вес единиц, входящих в интервал, в общем их объеме, % | Удельный вес единиц, входящих в интервал, при нормальном распределении, % |
| 1 | 2 | 3 | 4 |
| [m-s;m+s] | 68,3 | ||
| [m-2s;m+2s] | 95,4 | ||
| [m-3s;m+3s] | 99,7 |
Этап 3. Провести выравнивание данных по теоретической кривой нормального распределения и проверить соответствие данных нормальному закону с помощью критерия согласия Колмогорова. В качестве данных для проверки соответствия нормальному закону распределения выбрать один из рядов динамики по результатам выполнения лабораторной работы № 5, этап 4.
Теоретическая кривая распределения выражает функциональную связь между изменением варьирующего признака и частот, характеризующих определенный тип распределения. Для выравнивания данных по теоретической кривой нормального распределения необходимо провести последовательную обработку показателей ряда, по которому проводится проверка на соответствие нормальному закону распределения в соответствии с табл. 9.
Таблица 9
Выравнивание по кривой нормального распределения
| х | f |
|
| f(t) | Теоретические частоты f1(t) | Кумулятивные частоты |
| |
| фактич. | теор. | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Для заполнения таблицы необходимы данные по математическому ожиданию и среднему квадратическому отклонению показателя, для которого проводится проверка. В гр. 2 заносятся частоты появления отдельных вариант показателя, в гр. 4 рассчитывается нормированное отклонение по приведенной формуле. В пятую графу заносятся табличные значения функции f ( t ). В графе 6 исчислены теоретические значения кривой нормального распределения по формуле
f1( t )= f ( t )·постоянный множитель,
где постоянный множитель равен (n*i)/ s;
n – число наблюдений или сумма частот по гр. 2;
i – средний интервал между x;
s – среднее квадратическое отклонение в данном ряду.
Девятая графа демонстрирует разность между теоретическими и фактическими частотами распределения независимо от знака М. Эта разница является основой для подтверждения наличия нормального закона распределения с помощью критерия согласия.
Критерий согласия-это показатель, по которому можно судить, насколько теоретическое распределение близко к фактическому. Критерий согласия Колмогорова l равен максимальной разнице М, деленной на корень из числа наблюдений. По специальной таблице вероятностей для критерия согласия l, т.е. определяется вероятность, соответствующая полученному значению лямбда.
Если вероятность высокая, то с полученной вероятностью можно утверждать, что отклонения теоретических частот от фактических являются случайными, следовательно, можно считать, что в основе распределения данных лежит нормальный закон распределения.
Библиографический список
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики :Учеб. –М.: Финансы и статистика, 1995.
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учеб. –М.: ИНФА-М, 1998.
3. Общая теория статистики / Под ред. Л. М. Спирина. М.: Финансы и статистика, 1994.
4. Статистика: Текст лекций / Под ред. В. Г. Ионина. –М.: ИНФА-М, 1998.
5. Статистический анализ в экономике / Под ред. Г.Л. Громыко. – М.: Изд-во МГУ, 1992.
6. Четыркин Е.М. Статистические методы прогнозирования. – М.: Статистика, 1997.
7. Шураков В.В. и др. Автоматизированное рабочее место для статистической обработки данных. – М.: Финансы и статистика, 1990.
Учебное издание
Дата: 2019-03-05, просмотров: 344.