Цель работы: ознакомление с классификацией статистических наблюдений и освоение методов разработки программы статистических наблюдений.

Ход работы

     Этап 1. Изучить классификацию статистических наблюдений в соответствии со следующей схемой (рис. 2.1).

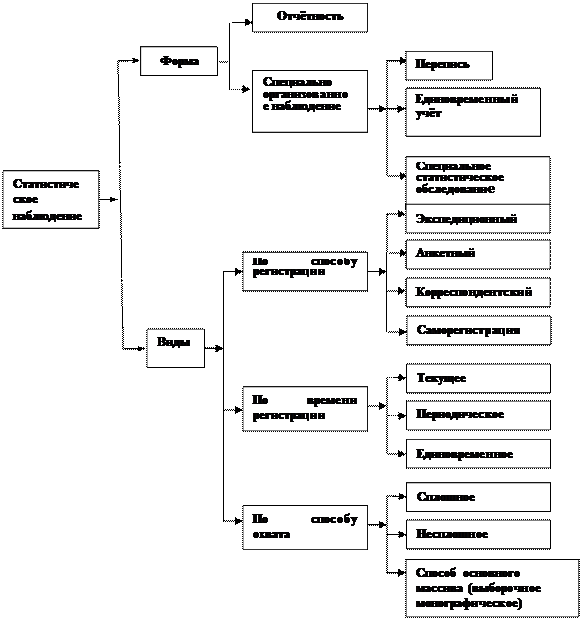Рис. 2.1

Описать характеристики статистического наблюдения, представленного в первой лабораторной работе, в соответствии с классификацией.

      Этап 2. Представить перечень показателей (вопросов), по которым можно разработать программу статистического наблюдения.

     Варианты экономических показателей:

1. Уровень успеваемости студенческой группы.

2. Культурно-массовые мероприятия в университете.

3. Уровень благосостояния семьи.

4. Показатели, характеризующие производительность труда на предприятии.

5. Финансовое состояние предприятия.

6. Уровень образованности жителей города.

7. Занятость населения города.

8. Демографическая ситуация в городе.

9. Спортивные достижения университета.

10.  Состояние основных фондов на предприятии.

     Этап 3. Разработать программу обследования численности и состава работников промышленного электроэнергетического предприятия города.

     Примечание. Программы обследования второго и третьего этапов должны включать 6–9 вопросов, ответы на которые позволяют накопить статистическую информацию по данному вопросу.

Лабораторная работа № 3

ИЗУЧЕНИЕ МЕТОДОВ РАСЧЕТА И ОСНОВНЫХ СВОЙСТВ СТЕПЕННЫХ СРЕДНИХ ВЕЛИЧИН

     Цель работы: ознакомление с порядком расчета и взаимосвязанностью степенных средних величин.

Ход работы

Этап 1. По значению любого количественного признака, представленного в анкете (лабораторная работа № 1), рассчитать все виды степенных средних в простой и взвешенной форме (табл. 2). Сделать вывод о соблюдении правила мажорантности степенных средних

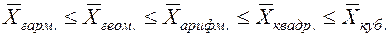
Таблица 2

Виды степенных средних

Вид степенной средней	Показатель степени m	Формула расчёта
		простая	взвешенная
Гармоническая	-1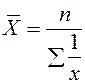
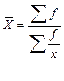
Геометрическая	0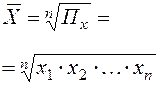
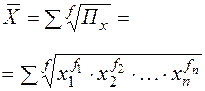
Арифметическая	1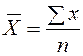
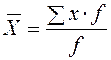
Квадратическая	2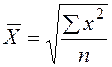
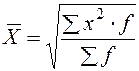
Кубическая	3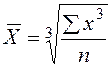

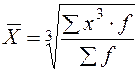
Этап 2. Проверить выполнение важнейших свойств средней арифметической.

     1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты:

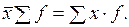
     2. Если от каждой варианты отнять какое-либо произвольное число, то новая средняя уменьшится на то же число:

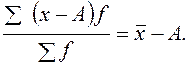
     3. Если к каждой варианте прибавить какое-либо произвольное число, то средняя увеличится на это же число:

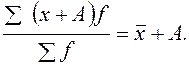
     4. Если каждую варианту разделить на какое-либо произвольное число, то средняя уменьшится во столько же раз:

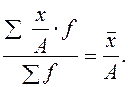
     5. Если каждую варианту умножить на какое-либо число, то средняя арифметическая увеличится во столько же раз:

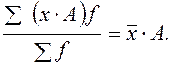
     6. Если все частоты (веса) разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится.

     7. Сумма отклонений вариант от средней арифметической всегда  равна 0:

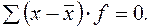
Лабораторная работа № 4