Цель работы: ознакомление с порядком расчета показателей вариации конкретного экономического показателя.
Ход работы
Этап 1. Рассчитать показатели вариации по данным двух рядов динамики (табл. 3.) по заданию преподавателя.
Для измерения вариации в статистике применяют несколько способов. Наиболее простым является расчет показателя размаха вариации Н как разницы между максимальным Хmax и минимальным Хmax наблюдаемыми значениями признака:
H = Хmax - Хmin.
Однако размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается.
Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – среднее линейное отклонение Л как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:
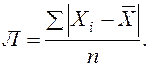
При повторяемости отдельных значений Х используют формулу средней арифметической взвешенной
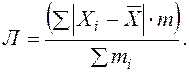
Напомним, что алгебраическая сумма отклонений от среднего уровня равна нулю.
Таблица 3
Исходные данные для прогнозирования развития отраслей топливно-энергетического комплекса Российской Федерации
| Показатель | Год | |||||||
| 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1.1.Производство первичных энергоресурсов по видам (млн т усл. топ.) | ||||||||
| Всего | 1862 | 1758 | 1656 | 1539 | 1438 | 1402 | 1396 | 1359 |
| в том числе: - нефть (включая - газовый конденсат) | 738 | 661 | 571 | 506 | 454 | 439 | 431 | 437 |
| - естественный газ | 739 | 742 | 740 | 713 | 698 | 685 | 694 | 659 |
| - уголь | 270 | 241 | 230 | 209 | 186 | 181 | 171 | 164 |
| - топливный торф (условной влажности) | 1,8 | 1,6 | 2,7 | 0,9 | 1,0 | 1,5 | 1,4 | 1,1 |
| - сланцы | 1,3 | 1,2 | 1,1 | 0,9 | 0,9 | 0,7 | 0,5 | 0,6 |
| - дрова | 17,2 | 17,5 | 13,4 | 13,7 | 8,5 | 8,1 | 7,0 | 6,0 |
| - электроэнергия, вырабатываемая ГЭС, АЭС и геотермальными электростанциями | 94,7 | 93,7 | 97,8 | 95,5 | 89,0 | 86,2 | 91,1 | 91,6 |
| 1.2. Установленная мощность электростанций (на конец года), млн кВт | ||||||||
| Всех электростанций | 213,3 | 213,0 | 212,0 | 213,4 | 214,9 | 215,0 | 214,5 | 214,2 |
| в том числе: ТЭС | 149,7 | 149,5 | 148,4 | 148,8 | 149,7 | 149,7 | 149,2 | 149,0 |
| ГЭС | 43,4 | 43,3 | 43,4 | 43,4 | 44,0 | 44,0 | 44,0 | 43,9 |
| АЭС | 20,2 | 20,2 | 20,2 | 21,2 | 21,2 | 21,3 | 21,3 | 21,3 |
| 1.3. Производство и потребление электроэнергии, млрд кВт·ч - произведено электроэнергии | 1082 | 1068 | 1008 | 956,6 | 875,9 | 860,0 | 847,2 | 834,1 |
| - получено из-за пределов РФ | 35,0 | 35,1 | 27,7 | 24,7 | 22,2 | 18,4 | 12,3 | 7,1 |
| - отпущено за пределы РФ | 43,4 | 47,2 | 44,0 | 43,4 | 41,7 | 38,0 | 31,8 | 26,8 |
| - потреблено электроэнергии всего | 1074 | 1056 | 992,2 | 937,9 | 856,4 | 840,4 | 827,7 | 814,4 |
| в том числе: Промышленностью | 625,9 | 605,2 | 554,6 | 512,8 | 447,0 | 440,2 | 424,9 | 421,4 |
| сельским хоз-вом | 96,4 | 103,4 | 102,9 | 103,8 | 97,7 | 88,6 | 85,9 | 78,1 |
| транспортом | 103,8 | 96,7 | 86,7 | 76,7 | 68,4 | 65,2 | 64,9 | 63,5 |
| другими отраслями | 247,7 | 250,8 | 247,9 | 244,6 | 243,3 | 246,4 | 252,0 | 251,4 |
| 1.4. Использование вторичных энергетических ресурсов - горючие, млн т усл. топ. | - | 14,4 | 13,2 | 10,8 | 9,8 | 13.3 | 9,2 | 11,8 |
| % от выхода | - | 90 | 90 | 92 | 92. | 95 | 94 | 95 |
| - тепловые, млн Гкал | - | 68,5 | 67,7 | 61,0 | 52,0 | 56,5 | 52,8 | 51,4 |
| % от выхода | - | 20 | 19 | 18 | 17 | 20 | 18 | 20 |
| - всего сэкономлено, млн т усл. топ. | - | 25,9 | 24,6 | 21,2 | 18,4 | 22,9 | 18,1 | 20,5 |
Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования. Но, к сожалению, этот показатель усложняет расчеты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии.
Дисперсия признака s2 определяется на основе квадратической степенной средней:
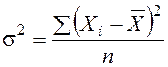 или
или 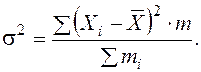
Показатель s, равный 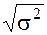 , называется средним квадратическим отклонением.
, называется средним квадратическим отклонением.
В общей теории статистики показатель дисперсии является оценкой одноименного показателя теории вероятностей и (как сумма квадратов отклонений) оценкой дисперсии в математической статистике, что позволяет использовать положения этих теоретических дисциплин для анализа социально-экономических процессов.
Простыми преобразованиями могут быть получены формулы расчета дисперсии методом моментов:
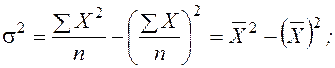

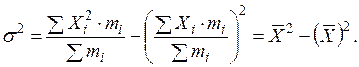
Здесь X2 – среднее значение квадратов признака, или начальный момент второго порядка; Х – среднее значение признака, или начальный момент первого порядка.
Коэффициент вариации 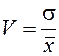 определяет степень колеблемости данных ряда динамики в соответствии с его численным значением:
определяет степень колеблемости данных ряда динамики в соответствии с его численным значением:
до 10 % – слабая колеблемость;
10¸25 % – умеренная колеблемость;
25¸100 % – сильная колеблемость данных рассматриваемо- го ряда динамики
Этап 2. Сделать вывод о степени колеблемости экономического показателя каждого ряда динамики. Провести сравнительную характеристику полученных показателей вариации.
Лабораторная работа № 5
ИЗУЧЕНИЕ РЯДОВ ДИНАМИКИ
Цель работы: ознакомление с порядком расчета показателей, характеризующих ряды динамики.
Ход работы
Этап 1. Рассчитать средние уровни по данным рядов динамики (табл. 3, лабораторная работа № 4).
Этап 2. По данным второго ряда динамики рассчитать все показатели анализа рядов. Порядок расчета показателей анализа ряда динамики представлен в табл. 4.
Таблица 4
Показатели анализа рядов динамики
| Показатель | Базисный | Цепной |
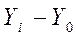 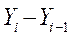 Абсолютный прирост
∆i баз; ∆i цеп Абсолютный прирост
∆i баз; ∆i цеп
| ||
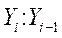 Коэффициент роста Kp Коэффициент роста Kp
| 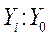
| 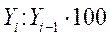
|
| Темп роста Тр | 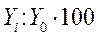
| |
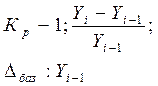 Коэффициент прироста Кпр Коэффициент прироста Кпр
| 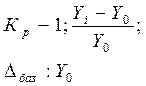
| |
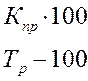 Темп прироста Тпр Темп прироста Тпр
| 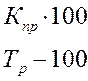
| 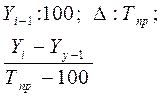
|
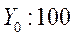 Абсолютное значение одного процента прироста А Абсолютное значение одного процента прироста А
| ∆i баз: Тпр |
Этап 3. Провести выравнивание двух заданных рядов методом наименьших квадратов по теоретическому уравнению регрессии y = a0 + ait.
Рассмотрим реализацию метода наименьших квадратов для линейной зависимости.
y = a0+a1t.
Данное уравнение можно классифицировать как линейную форму. Составим систему нормальных уравнений вида
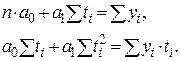
Определяем неизвестные параметры a0 и a1 на основе решения этой системы уравнений методом подстановки. Расчёт промежуточных параметров, необходимых для решения системы уравнений, можно оформить в виде таблицы (табл. 5).
Таблица 5
Обработка исходных данных для реализации метода наименьших квадратов
| Обозначение параметров | Значение по временным интервалам i =1..n | Сумма по интервалам | |||
| yi | y1 | y2 | … | yn | Σ yi |
| ti | 1 | 2 | … | n | Σ ti |
| ti2 | 1*1 | 2*2 | … | n*n | Σ ti2 |
| yi*ti | y1*1 | y2*2 | … | yn*n | Σ yi*ti |
Этап 4. По полученным уравнениям трендов определить прогнозные значения показателей двух заданных рядов динамики до 2010 года.
Лабораторная работа № 6
Дата: 2019-03-05, просмотров: 354.