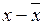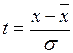МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ЛАБОРАТОРНЫМ РАБОТАМ ПО ДИСЦИПЛИНЕ
“СТАТИСТИКА”
Новочеркасск 2005

УДК 311(076.5)
Рецензент канд. экон. наук, доц. В.В. Кощей
Составитель И.В. Зайцева
Методические указания к лабораторным работам по дисциплине “Статистика” / Юж.-Рос. гос. техн. ун-т. – Новочеркасск: ЮРГТУ, 2005. – 17с.
Практические задания, выполняемые на лабораторных занятиях, позволяют глубже разобраться в методике расчета конкретных статистических показателей. Методические указания предназначены для студентов специальности 0648000 “Экономика и управление на предприятии (в электроэнергетике)”. И могут быть рекомендованы для выполнения индивидуальных заданий слушателями второго высшего образования по данной дисциплине.
Ó Южно-Российский государственный
технический университет, 2005
Ó Зайцева И.В., 2005
Лабораторная работа № 1
СБОР И ПЕРВИЧНАЯ ОБРАБОТКА СТАТИСТИЧЕСКИХ ДАННЫХ
Цель работы: ознакомление с приемами сбора информации и методами первичной обработки статистических данных.
Ход работы
Этап.1. Сформировать анкету, позволяющую собрать статистические сведения о населении по некоторой группе (сотрудники отдела, лаборатории, студенты группы и т.д.). Заполнить анкету по форме, представленной в табл. 1.
Таблица 1
Анкета для обследования населения
| Перечень обследуемых | Признаки, по которым проводится обследование | |||
| Примеры признаков «пол», «возраст», «образование», «семейное положение» и т.д. | ||||
Примечание. Для того, чтобы делать выводы по результатам обследования населения, необходимо опросить около 20 человек по 4–5 признакам.
Этап 2. Выработать значения признаков обследования населения (табл. 1) по следующей схеме.
1. Численная обработка результатов анкеты.
Пример обработки
Признак «пол»
| Варианты признака | Количество единиц совокупности данного признака, чел. | Значение, % |
| Мужской Женский | 15 5 | 75 25 |
| ИТОГО | 20 | 100 |
Этап 3. Графическая обработка результатов анкеты.
Для графического изображения статистических данных используются самые разнообразные виды графиков. При этом наилучшее соотношение масштаба по осям абсцисс и ординат, равное 1,62:1, называется «Золотым сечением»
Линейные диаграммы применяются для характеристики динамики, т.е. оценки изменения явлений во времени; для характеристики вариации в рядах распределения; для оценки выполнения плановых заданий; для оценки взаимосвязи между явлениями. Они строятся в прямоугольной системе координат. По оси абсцисс откладываются отрезки, соответствующие датам или периодам времени, по оси ординат – уровни ряда динамики или темпы их изменения. Полученные точки соединяются отрезками в виде ломаной линии. Каждая точка линейной диаграммы соответствует уровню динамического ряда (или темпу его изменения) на определённый момент или за период времени. На одном графике может быть размещено несколько диаграмм, что позволяет сравнивать динамику различных показателей либо одного показателя по разным регионам или странам.
Столбиковые диаграммы . Столбики располагаются вплотную или раздельно на одинаковом расстоянии. Они имеют одинаковое основание, а их высота должна быть пропорциональна числовым значениям уровней признака. По высоте столбиков этой диаграммы определяют соотношение между уровнями изучаемых показателей.
Секторные диаграммы . Анализ структуры проводится на основе сопоставления различных частей целого при помощи площадей, образуемых секторами круга. Для построения этой диаграммы круг следует разделить на секторы пропорционально удельному весу частей в целом. Сумма удельных весов равна 100 %, что соответствует общему объему изучаемого явления. Размер каждого сектора определяется по величине угла с учётом того, что 1 % соответствует 3,6".
Полосовые диаграммы состоят из прямоугольников, расположенных горизонтально (полосами, лентами). Масштабная шкала этих графиков находится на горизонтальной оси. Принцип построения полосовых диаграмм тот же, что и столбиковых диаграмм.
Иногда для целей сравнительного анализа по регионам, странам используют квадратные, круговые, фигурные диаграммы (диаграммы фигур-знаков). Диаграммы геометрических фигур отражают размер изучаемогообъекта в соответствии с размером своей площади. Для построения квадратной диаграммы, применяемой при сравнительном анализе, следует извлечь квадратные корни из сравниваемых величин статистических показателей, а затем построить квадраты со сторонами, пропорциональными полученным результатам. При построении круговой диаграммы значения показателей вначале делят на число p, т.е. 3,14, а затем из полученных величин извлекают квадратные корни и строят круги с радиусами, пропорциональными полученным результатам. Диаграммы фигур-знаков представляют собой графические изображения в виде рисунков, силуэтов, фигур, соответствующих содержанию статистических данных. Рисунки отличаются друг от друга размером (соответственно величине показателя), либо величины статистических показателей изображаются на рисунках определенным количеством одинаковых по размеру и типу фигур.
Для оценки географического размещения явлений, сравнительного анализа по территориям применяются статистические карты. Они достаточно часто используются в публикациях ООН.
Статистические карты включают картограммы и картодиаграммы. Картограмма показывает территориальное распределение изучаемого признака по отдельным районам и используется для выявления закономерностей этого распределения. Картограммы бывают фоновые и точечные. Фоновые картограммы разной густотой цветовой окраски характеризуют распределение изучаемого признака на различных территориях.
На точечной картограмме каждой точке соответствует одно и то же принятое числовое значение, например равное 100 т. Нанося на контур каждого района соответствующее количество точек, мы получаем точечную картограмму, характеризующую распределение изучаемого признака по районам. Как правило, фоновые картограммы используются при анализе статистических показателей в виде относительных и средних величин, в то время как точечные – для характеристики размещения абсолютных величин.
Картодиаграмма – представляет собой сочетание диаграммы с географической картой. Она позволяет отразить специфику каждого района в распределении изучаемого явления, его структурные особенности.
По вышеприведенной схеме обрабатываются данные по 4–5 признакам, представленным в анкете.
Лабораторная работа должна заканчиваться кратким выводом по полученным результатам.
Лабораторная работа № 2
Ход работы
Этап 1. Изучить классификацию статистических наблюдений в соответствии со следующей схемой (рис. 2.1).
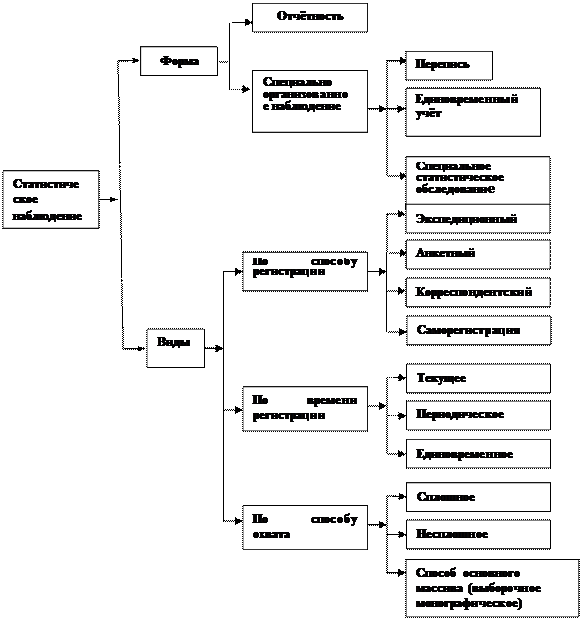 |
Рис. 2.1
Описать характеристики статистического наблюдения, представленного в первой лабораторной работе, в соответствии с классификацией.
Этап 2. Представить перечень показателей (вопросов), по которым можно разработать программу статистического наблюдения.
Варианты экономических показателей:
1. Уровень успеваемости студенческой группы.
2. Культурно-массовые мероприятия в университете.
3. Уровень благосостояния семьи.
4. Показатели, характеризующие производительность труда на предприятии.
5. Финансовое состояние предприятия.
6. Уровень образованности жителей города.
7. Занятость населения города.
8. Демографическая ситуация в городе.
9. Спортивные достижения университета.
10. Состояние основных фондов на предприятии.
Этап 3. Разработать программу обследования численности и состава работников промышленного электроэнергетического предприятия города.
Примечание. Программы обследования второго и третьего этапов должны включать 6–9 вопросов, ответы на которые позволяют накопить статистическую информацию по данному вопросу.
Лабораторная работа № 3
Ход работы
Этап 1. По значению любого количественного признака, представленного в анкете (лабораторная работа № 1), рассчитать все виды степенных средних в простой и взвешенной форме (табл. 2). Сделать вывод о соблюдении правила мажорантности степенных средних
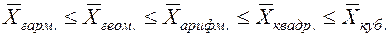
Таблица 2
Виды степенных средних
| Вид степенной средней | Показатель степени m | Формула расчёта | |
| простая | взвешенная | ||
| Гармоническая | -1 | 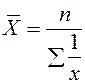
| 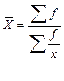
|
| Геометрическая | 0 | 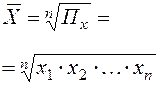
| 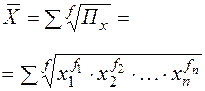
|
| Арифметическая | 1 | 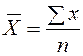
| 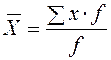
|
| Квадратическая | 2 | 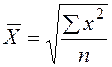
| 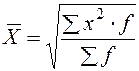
|
| Кубическая | 3 | 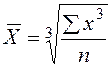
| 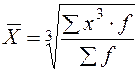
|
Этап 2. Проверить выполнение важнейших свойств средней арифметической.
1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты:
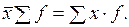
2. Если от каждой варианты отнять какое-либо произвольное число, то новая средняя уменьшится на то же число:
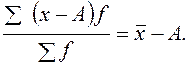
3. Если к каждой варианте прибавить какое-либо произвольное число, то средняя увеличится на это же число:
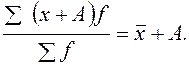
4. Если каждую варианту разделить на какое-либо произвольное число, то средняя уменьшится во столько же раз:
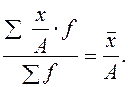
5. Если каждую варианту умножить на какое-либо число, то средняя арифметическая увеличится во столько же раз:
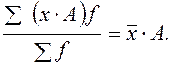
6. Если все частоты (веса) разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится.
7. Сумма отклонений вариант от средней арифметической всегда равна 0:
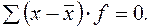
Лабораторная работа № 4
Ход работы
Этап 1. Рассчитать показатели вариации по данным двух рядов динамики (табл. 3.) по заданию преподавателя.
Для измерения вариации в статистике применяют несколько способов. Наиболее простым является расчет показателя размаха вариации Н как разницы между максимальным Хmax и минимальным Хmax наблюдаемыми значениями признака:
H = Хmax - Хmin.
Однако размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается.
Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – среднее линейное отклонение Л как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:
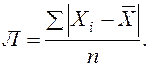
При повторяемости отдельных значений Х используют формулу средней арифметической взвешенной
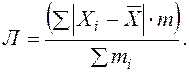
Напомним, что алгебраическая сумма отклонений от среднего уровня равна нулю.
Таблица 3
Исходные данные для прогнозирования развития отраслей топливно-энергетического комплекса Российской Федерации
| Показатель | Год | |||||||
| 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1.1.Производство первичных энергоресурсов по видам (млн т усл. топ.) | ||||||||
| Всего | 1862 | 1758 | 1656 | 1539 | 1438 | 1402 | 1396 | 1359 |
| в том числе: - нефть (включая - газовый конденсат) | 738 | 661 | 571 | 506 | 454 | 439 | 431 | 437 |
| - естественный газ | 739 | 742 | 740 | 713 | 698 | 685 | 694 | 659 |
| - уголь | 270 | 241 | 230 | 209 | 186 | 181 | 171 | 164 |
| - топливный торф (условной влажности) | 1,8 | 1,6 | 2,7 | 0,9 | 1,0 | 1,5 | 1,4 | 1,1 |
| - сланцы | 1,3 | 1,2 | 1,1 | 0,9 | 0,9 | 0,7 | 0,5 | 0,6 |
| - дрова | 17,2 | 17,5 | 13,4 | 13,7 | 8,5 | 8,1 | 7,0 | 6,0 |
| - электроэнергия, вырабатываемая ГЭС, АЭС и геотермальными электростанциями | 94,7 | 93,7 | 97,8 | 95,5 | 89,0 | 86,2 | 91,1 | 91,6 |
| 1.2. Установленная мощность электростанций (на конец года), млн кВт | ||||||||
| Всех электростанций | 213,3 | 213,0 | 212,0 | 213,4 | 214,9 | 215,0 | 214,5 | 214,2 |
| в том числе: ТЭС | 149,7 | 149,5 | 148,4 | 148,8 | 149,7 | 149,7 | 149,2 | 149,0 |
| ГЭС | 43,4 | 43,3 | 43,4 | 43,4 | 44,0 | 44,0 | 44,0 | 43,9 |
| АЭС | 20,2 | 20,2 | 20,2 | 21,2 | 21,2 | 21,3 | 21,3 | 21,3 |
| 1.3. Производство и потребление электроэнергии, млрд кВт·ч - произведено электроэнергии | 1082 | 1068 | 1008 | 956,6 | 875,9 | 860,0 | 847,2 | 834,1 |
| - получено из-за пределов РФ | 35,0 | 35,1 | 27,7 | 24,7 | 22,2 | 18,4 | 12,3 | 7,1 |
| - отпущено за пределы РФ | 43,4 | 47,2 | 44,0 | 43,4 | 41,7 | 38,0 | 31,8 | 26,8 |
| - потреблено электроэнергии всего | 1074 | 1056 | 992,2 | 937,9 | 856,4 | 840,4 | 827,7 | 814,4 |
| в том числе: Промышленностью | 625,9 | 605,2 | 554,6 | 512,8 | 447,0 | 440,2 | 424,9 | 421,4 |
| сельским хоз-вом | 96,4 | 103,4 | 102,9 | 103,8 | 97,7 | 88,6 | 85,9 | 78,1 |
| транспортом | 103,8 | 96,7 | 86,7 | 76,7 | 68,4 | 65,2 | 64,9 | 63,5 |
| другими отраслями | 247,7 | 250,8 | 247,9 | 244,6 | 243,3 | 246,4 | 252,0 | 251,4 |
| 1.4. Использование вторичных энергетических ресурсов - горючие, млн т усл. топ. | - | 14,4 | 13,2 | 10,8 | 9,8 | 13.3 | 9,2 | 11,8 |
| % от выхода | - | 90 | 90 | 92 | 92. | 95 | 94 | 95 |
| - тепловые, млн Гкал | - | 68,5 | 67,7 | 61,0 | 52,0 | 56,5 | 52,8 | 51,4 |
| % от выхода | - | 20 | 19 | 18 | 17 | 20 | 18 | 20 |
| - всего сэкономлено, млн т усл. топ. | - | 25,9 | 24,6 | 21,2 | 18,4 | 22,9 | 18,1 | 20,5 |
Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования. Но, к сожалению, этот показатель усложняет расчеты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии.
Дисперсия признака s2 определяется на основе квадратической степенной средней:
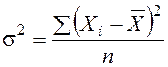 или
или 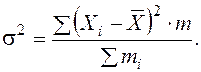
Показатель s, равный 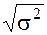 , называется средним квадратическим отклонением.
, называется средним квадратическим отклонением.
В общей теории статистики показатель дисперсии является оценкой одноименного показателя теории вероятностей и (как сумма квадратов отклонений) оценкой дисперсии в математической статистике, что позволяет использовать положения этих теоретических дисциплин для анализа социально-экономических процессов.
Простыми преобразованиями могут быть получены формулы расчета дисперсии методом моментов:
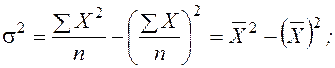

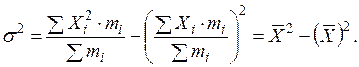
Здесь X2 – среднее значение квадратов признака, или начальный момент второго порядка; Х – среднее значение признака, или начальный момент первого порядка.
Коэффициент вариации 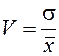 определяет степень колеблемости данных ряда динамики в соответствии с его численным значением:
определяет степень колеблемости данных ряда динамики в соответствии с его численным значением:
до 10 % – слабая колеблемость;
10¸25 % – умеренная колеблемость;
25¸100 % – сильная колеблемость данных рассматриваемо- го ряда динамики
Этап 2. Сделать вывод о степени колеблемости экономического показателя каждого ряда динамики. Провести сравнительную характеристику полученных показателей вариации.
Лабораторная работа № 5
ИЗУЧЕНИЕ РЯДОВ ДИНАМИКИ
Цель работы: ознакомление с порядком расчета показателей, характеризующих ряды динамики.
Ход работы
Этап 1. Рассчитать средние уровни по данным рядов динамики (табл. 3, лабораторная работа № 4).
Этап 2. По данным второго ряда динамики рассчитать все показатели анализа рядов. Порядок расчета показателей анализа ряда динамики представлен в табл. 4.
Таблица 4
Показатели анализа рядов динамики
| Показатель | Базисный | Цепной |
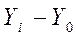 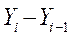 Абсолютный прирост
∆i баз; ∆i цеп Абсолютный прирост
∆i баз; ∆i цеп
| ||
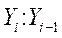 Коэффициент роста Kp Коэффициент роста Kp
| 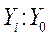
| 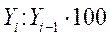
|
| Темп роста Тр | 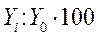
| |
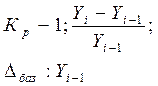 Коэффициент прироста Кпр Коэффициент прироста Кпр
| 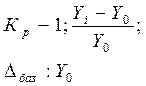
| |
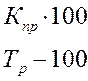 Темп прироста Тпр Темп прироста Тпр
| 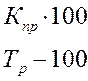
| 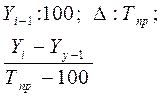
|
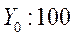 Абсолютное значение одного процента прироста А Абсолютное значение одного процента прироста А
| ∆i баз: Тпр |
Этап 3. Провести выравнивание двух заданных рядов методом наименьших квадратов по теоретическому уравнению регрессии y = a0 + ait.
Рассмотрим реализацию метода наименьших квадратов для линейной зависимости.
y = a0+a1t.
Данное уравнение можно классифицировать как линейную форму. Составим систему нормальных уравнений вида
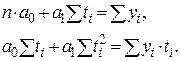
Определяем неизвестные параметры a0 и a1 на основе решения этой системы уравнений методом подстановки. Расчёт промежуточных параметров, необходимых для решения системы уравнений, можно оформить в виде таблицы (табл. 5).
Таблица 5
Обработка исходных данных для реализации метода наименьших квадратов
| Обозначение параметров | Значение по временным интервалам i =1..n | Сумма по интервалам | |||
| yi | y1 | y2 | … | yn | Σ yi |
| ti | 1 | 2 | … | n | Σ ti |
| ti2 | 1*1 | 2*2 | … | n*n | Σ ti2 |
| yi*ti | y1*1 | y2*2 | … | yn*n | Σ yi*ti |
Этап 4. По полученным уравнениям трендов определить прогнозные значения показателей двух заданных рядов динамики до 2010 года.
Лабораторная работа № 6
Ход работы
Этап 1. Рассчитать и проанализировать значение линейного коэффициента корреляции, характеризующего связь между показателями, представленными двумя рядами (лабораторная работа № 5, прогнозные данные до 2010 года).
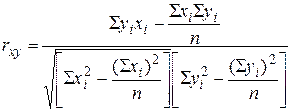 Линейный коэффициент корреляции принимает значения в интервале от - 1 до + 1. Принято считать, что если | r | < 0,30, то связь слабая, при | r | = = (0,3 + 0,7) – средняя, при | r | > 0,70 – сильная, или тесная. Когда | r | = 1 – связь функциональная. Если же r ≈ 0, то это дает основание говорить об отсутствии линейной связи между У и X. Коэффициент корреляции считается по нижеприведенной формуле
Линейный коэффициент корреляции принимает значения в интервале от - 1 до + 1. Принято считать, что если | r | < 0,30, то связь слабая, при | r | = = (0,3 + 0,7) – средняя, при | r | > 0,70 – сильная, или тесная. Когда | r | = 1 – связь функциональная. Если же r ≈ 0, то это дает основание говорить об отсутствии линейной связи между У и X. Коэффициент корреляции считается по нижеприведенной формуле
|
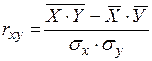 .
.
Можно использовать и другие формулы, но результат должен быть одинаковым для всех вариантов расчета.
Этап 2. Провести выравнивание рядов методом наименьших квадратов по теоретическому уравнению регрессии y=a0 + a1x.
Для системы уравнений
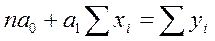 ,
,
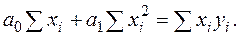
Метод наименьших квадратов применяется для определения параметров а0 и а1.
Смысл параметров:
а1 – это коэффициент регрессии, характеризующий влияние, которое оказывает изменение X на Y, т.е. объем выпущенной продукции на величину заработной платы, а1 показывает, на сколько единиц в среднем изменится Y при изменении X на единицу. Если а1> 0, то наблюдается положительная связь. Если а1< 0, то увеличение Х на единицу влечет за собой уменьшение Y в среднем на а1 (параметр а1 обладает размерностью отношения Y к Х).
Параметр а0 – это постоянная величина в уравнении регрессии, часто экономического смысла не имеет, но в ряде случаев ее интерпретируют как начальное значение Y.
Значение функции y=a0+a1х называется расчетным значением и на графике образует теоретическую линию регрессии. Смысл теоретической регрессии заключается в том, что это оценка среднего значения переменной Y для заданного значения Х.
Построить график теоретической прямой регрессии.
Этап 3. На основе полученного уравнения регрессии рассчитать значение корреляционного отношения и коэффициента детерминации и сделать вывод о степени связи между исследуемыми показателями.
Рассмотрим метод расчета коэффициента детерминации на основе уравнения парной линейной регрессии Ỹi=a0+a1·Xi. Анализ уравнения регрессии позволяет оценить роль исследуемого факторного признака в формировании результативного. Для этого необходимо определить долю фактора в общей изменчивости вариации результативного признака.
Рассмотрим метод разложения вариации по факторам.
Вариация любого показателя оценивается дисперсией. Для результата Y дисперсия s2носит название общей и обозначается s2общ (y):
s2общ (y)=М(у2)-[M(y)]2,
где М – математическое ожидание.
Далее для последовательной оценки вариации по сформированному уравнению регрессии нужно рассчитать теоретические значения результата. Обычно этот расчет оформляется в виде табл. 6.
Таблица 6
Расчет теоретических значений признака - результата
| Номер наблюдения | Значения Хi | Теоретические значения Ỹi=a0+a1·Xi | Ỹi2 |
| 1 | |||
| 2 | |||
| … | |||
| 20÷25 |
Далее оценивается так называемая факторная дисперсия
s2факт (Ỹ)=M(Ỹ2)-[M(Ỹ)]2.
Кроме представленного в данном уравнении регрессии фактора на конечный результат влияют другие факторы. Это влияние случайно. Дисперсию, вызываемую влиянием этих случайных факторов, называют остаточной:
s2ост (Y)= s2 общ (Y)- s2 факт (Ỹ).
Таким образом,
s2общ (Y)= s2факт (Ỹ)+ s2ост (Y).
Отношение 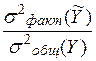 показывает долю факторной вариации в общей. Если это отношение равно 1, то результат Y полностью зависит только от влияния данного рассматриваемого фактора. Если это отношение равно 0, то данный результат зависит от случайных факторов.
показывает долю факторной вариации в общей. Если это отношение равно 1, то результат Y полностью зависит только от влияния данного рассматриваемого фактора. Если это отношение равно 0, то данный результат зависит от случайных факторов.
В экономическом анализе это отношение имеет особое значение и называется отношением детерминации:
η2= 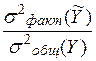 .
.
По нашим рассуждениям получаем
η2+ 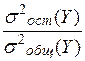 =1.
=1.
Отсюда получаем
η2=1- 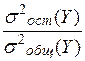 .
.
Это преобразование сделано для расчета так называемого коэффициента детерминации, который является универсальным показателем для оценки связи между исследуемыми признаками. Определяется он по формуле
η= 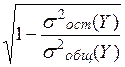 .
.
Границы изменения η от 0 до 1. Если η=1, то в наличии полная функциональная связь признака результата и признака фактора. Если η=0 – связь не обнаруживается. Коэффициент детерминации является универсальным потому, что он не зависит от вида связи между X и Y.
Лабораторная работа № 7
Ход работы
Этап 1. На основе данных о возрастном составе рабочих (лет): 18; 38; 28; 29; 26; 38; 34; 22; 28; 30; 22; 23; 35; 33; 27; 24; 30; 32; 28; 25; 29; 26; 31; 24; 29; 27; 32; 25; 29; 29 разработать интервальный ряд распределения и обработать исходные данные по следующей схеме (табл. 7):
Таблица 7
Интервальный ряд распределения
| Группы рабочих по возрасту (лет) x | Число рабочих f | Накопленная частота S |
| … | … | … |
| Итого |
Этап 2. Построить гистограмму распределения данных. Проверить нормальность распределения исследуемого факторного признака с помощью правила «трех сигм» (предварительно необходимо определить математическое ожидание m и среднее квадратическое отклонение s исследуемых данных).
Правило «трех сигм» определяет, что для нормально распределенной
случайной величины все рассеивание с точностью до долей процента укладывается на участке m ±3s. Это позволяет, зная s и m случайной величины, ориентировочно указать интервал ее практически возможных значений.
Правило трех сигм как способ оценки диапазона возможных значений случайной величины позволяет формировать интервал возможного изменения случайной величины [m-3 s; m+3 s] .
Результаты проверки на нормальность распределения представить в табличной форме (табл. 8).
Таблица 8
Проверка данных на соответствие нормальному закону распределения
| Интервалы значений признака | Число единиц, входящих в интервал | Удельный вес единиц, входящих в интервал, в общем их объеме, % | Удельный вес единиц, входящих в интервал, при нормальном распределении, % |
| 1 | 2 | 3 | 4 |
| [m-s;m+s] | 68,3 | ||
| [m-2s;m+2s] | 95,4 | ||
| [m-3s;m+3s] | 99,7 |
Этап 3. Провести выравнивание данных по теоретической кривой нормального распределения и проверить соответствие данных нормальному закону с помощью критерия согласия Колмогорова. В качестве данных для проверки соответствия нормальному закону распределения выбрать один из рядов динамики по результатам выполнения лабораторной работы № 5, этап 4.
Теоретическая кривая распределения выражает функциональную связь между изменением варьирующего признака и частот, характеризующих определенный тип распределения. Для выравнивания данных по теоретической кривой нормального распределения необходимо провести последовательную обработку показателей ряда, по которому проводится проверка на соответствие нормальному закону распределения в соответствии с табл. 9.
Таблица 9
Выравнивание по кривой нормального распределения
| х | f |
|
| f(t) | Теоретические частоты f1(t) | Кумулятивные частоты |
| |
| фактич. | теор. | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Для заполнения таблицы необходимы данные по математическому ожиданию и среднему квадратическому отклонению показателя, для которого проводится проверка. В гр. 2 заносятся частоты появления отдельных вариант показателя, в гр. 4 рассчитывается нормированное отклонение по приведенной формуле. В пятую графу заносятся табличные значения функции f ( t ). В графе 6 исчислены теоретические значения кривой нормального распределения по формуле
f1( t )= f ( t )·постоянный множитель,
где постоянный множитель равен (n*i)/ s;
n – число наблюдений или сумма частот по гр. 2;
i – средний интервал между x;
s – среднее квадратическое отклонение в данном ряду.
Девятая графа демонстрирует разность между теоретическими и фактическими частотами распределения независимо от знака М. Эта разница является основой для подтверждения наличия нормального закона распределения с помощью критерия согласия.
Критерий согласия-это показатель, по которому можно судить, насколько теоретическое распределение близко к фактическому. Критерий согласия Колмогорова l равен максимальной разнице М, деленной на корень из числа наблюдений. По специальной таблице вероятностей для критерия согласия l, т.е. определяется вероятность, соответствующая полученному значению лямбда.
Если вероятность высокая, то с полученной вероятностью можно утверждать, что отклонения теоретических частот от фактических являются случайными, следовательно, можно считать, что в основе распределения данных лежит нормальный закон распределения.
Библиографический список
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики :Учеб. –М.: Финансы и статистика, 1995.
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учеб. –М.: ИНФА-М, 1998.
3. Общая теория статистики / Под ред. Л. М. Спирина. М.: Финансы и статистика, 1994.
4. Статистика: Текст лекций / Под ред. В. Г. Ионина. –М.: ИНФА-М, 1998.
5. Статистический анализ в экономике / Под ред. Г.Л. Громыко. – М.: Изд-во МГУ, 1992.
6. Четыркин Е.М. Статистические методы прогнозирования. – М.: Статистика, 1997.
7. Шураков В.В. и др. Автоматизированное рабочее место для статистической обработки данных. – М.: Финансы и статистика, 1990.
Учебное издание
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ЛАБОРАТОРНЫМ РАБОТАМ ПО ДИСЦИПЛИНЕ
“СТАТИСТИКА”
Новочеркасск 2005

УДК 311(076.5)
Рецензент канд. экон. наук, доц. В.В. Кощей
Составитель И.В. Зайцева
Методические указания к лабораторным работам по дисциплине “Статистика” / Юж.-Рос. гос. техн. ун-т. – Новочеркасск: ЮРГТУ, 2005. – 17с.
Практические задания, выполняемые на лабораторных занятиях, позволяют глубже разобраться в методике расчета конкретных статистических показателей. Методические указания предназначены для студентов специальности 0648000 “Экономика и управление на предприятии (в электроэнергетике)”. И могут быть рекомендованы для выполнения индивидуальных заданий слушателями второго высшего образования по данной дисциплине.
Ó Южно-Российский государственный
технический университет, 2005
Ó Зайцева И.В., 2005
Лабораторная работа № 1
СБОР И ПЕРВИЧНАЯ ОБРАБОТКА СТАТИСТИЧЕСКИХ ДАННЫХ
Цель работы: ознакомление с приемами сбора информации и методами первичной обработки статистических данных.
Ход работы
Этап.1. Сформировать анкету, позволяющую собрать статистические сведения о населении по некоторой группе (сотрудники отдела, лаборатории, студенты группы и т.д.). Заполнить анкету по форме, представленной в табл. 1.
Таблица 1
Анкета для обследования населения
| Перечень обследуемых | Признаки, по которым проводится обследование | |||
| Примеры признаков «пол», «возраст», «образование», «семейное положение» и т.д. | ||||
Примечание. Для того, чтобы делать выводы по результатам обследования населения, необходимо опросить около 20 человек по 4–5 признакам.
Этап 2. Выработать значения признаков обследования населения (табл. 1) по следующей схеме.
1. Численная обработка результатов анкеты.
Пример обработки
Признак «пол»
| Варианты признака | Количество единиц совокупности данного признака, чел. | Значение, % |
| Мужской Женский | 15 5 | 75 25 |
| ИТОГО | 20 | 100 |
Этап 3. Графическая обработка результатов анкеты.
Для графического изображения статистических данных используются самые разнообразные виды графиков. При этом наилучшее соотношение масштаба по осям абсцисс и ординат, равное 1,62:1, называется «Золотым сечением»
Линейные диаграммы применяются для характеристики динамики, т.е. оценки изменения явлений во времени; для характеристики вариации в рядах распределения; для оценки выполнения плановых заданий; для оценки взаимосвязи между явлениями. Они строятся в прямоугольной системе координат. По оси абсцисс откладываются отрезки, соответствующие датам или периодам времени, по оси ординат – уровни ряда динамики или темпы их изменения. Полученные точки соединяются отрезками в виде ломаной линии. Каждая точка линейной диаграммы соответствует уровню динамического ряда (или темпу его изменения) на определённый момент или за период времени. На одном графике может быть размещено несколько диаграмм, что позволяет сравнивать динамику различных показателей либо одного показателя по разным регионам или странам.
Столбиковые диаграммы . Столбики располагаются вплотную или раздельно на одинаковом расстоянии. Они имеют одинаковое основание, а их высота должна быть пропорциональна числовым значениям уровней признака. По высоте столбиков этой диаграммы определяют соотношение между уровнями изучаемых показателей.
Секторные диаграммы . Анализ структуры проводится на основе сопоставления различных частей целого при помощи площадей, образуемых секторами круга. Для построения этой диаграммы круг следует разделить на секторы пропорционально удельному весу частей в целом. Сумма удельных весов равна 100 %, что соответствует общему объему изучаемого явления. Размер каждого сектора определяется по величине угла с учётом того, что 1 % соответствует 3,6".
Полосовые диаграммы состоят из прямоугольников, расположенных горизонтально (полосами, лентами). Масштабная шкала этих графиков находится на горизонтальной оси. Принцип построения полосовых диаграмм тот же, что и столбиковых диаграмм.
Иногда для целей сравнительного анализа по регионам, странам используют квадратные, круговые, фигурные диаграммы (диаграммы фигур-знаков). Диаграммы геометрических фигур отражают размер изучаемогообъекта в соответствии с размером своей площади. Для построения квадратной диаграммы, применяемой при сравнительном анализе, следует извлечь квадратные корни из сравниваемых величин статистических показателей, а затем построить квадраты со сторонами, пропорциональными полученным результатам. При построении круговой диаграммы значения показателей вначале делят на число p, т.е. 3,14, а затем из полученных величин извлекают квадратные корни и строят круги с радиусами, пропорциональными полученным результатам. Диаграммы фигур-знаков представляют собой графические изображения в виде рисунков, силуэтов, фигур, соответствующих содержанию статистических данных. Рисунки отличаются друг от друга размером (соответственно величине показателя), либо величины статистических показателей изображаются на рисунках определенным количеством одинаковых по размеру и типу фигур.
Для оценки географического размещения явлений, сравнительного анализа по территориям применяются статистические карты. Они достаточно часто используются в публикациях ООН.
Статистические карты включают картограммы и картодиаграммы. Картограмма показывает территориальное распределение изучаемого признака по отдельным районам и используется для выявления закономерностей этого распределения. Картограммы бывают фоновые и точечные. Фоновые картограммы разной густотой цветовой окраски характеризуют распределение изучаемого признака на различных территориях.
На точечной картограмме каждой точке соответствует одно и то же принятое числовое значение, например равное 100 т. Нанося на контур каждого района соответствующее количество точек, мы получаем точечную картограмму, характеризующую распределение изучаемого признака по районам. Как правило, фоновые картограммы используются при анализе статистических показателей в виде относительных и средних величин, в то время как точечные – для характеристики размещения абсолютных величин.
Картодиаграмма – представляет собой сочетание диаграммы с географической картой. Она позволяет отразить специфику каждого района в распределении изучаемого явления, его структурные особенности.
По вышеприведенной схеме обрабатываются данные по 4–5 признакам, представленным в анкете.
Лабораторная работа должна заканчиваться кратким выводом по полученным результатам.
Лабораторная работа № 2
Дата: 2019-03-05, просмотров: 384.