Цель работы. Познакомиться с порядком построения линейного уравнения регрессии и расчета коэффициентов корреляционной связи.
Ход работы
Этап 1. Рассчитать и проанализировать значение линейного коэффициента корреляции, характеризующего связь между показателями, представленными двумя рядами (лабораторная работа № 5, прогнозные данные до 2010 года).
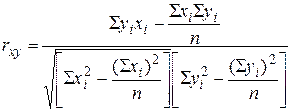 Линейный коэффициент корреляции принимает значения в интервале от - 1 до + 1. Принято считать, что если | r | < 0,30, то связь слабая, при | r | = = (0,3 + 0,7) – средняя, при | r | > 0,70 – сильная, или тесная. Когда | r | = 1 – связь функциональная. Если же r ≈ 0, то это дает основание говорить об отсутствии линейной связи между У и X. Коэффициент корреляции считается по нижеприведенной формуле
Линейный коэффициент корреляции принимает значения в интервале от - 1 до + 1. Принято считать, что если | r | < 0,30, то связь слабая, при | r | = = (0,3 + 0,7) – средняя, при | r | > 0,70 – сильная, или тесная. Когда | r | = 1 – связь функциональная. Если же r ≈ 0, то это дает основание говорить об отсутствии линейной связи между У и X. Коэффициент корреляции считается по нижеприведенной формуле
|
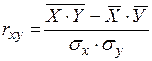 .
.
Можно использовать и другие формулы, но результат должен быть одинаковым для всех вариантов расчета.
Этап 2. Провести выравнивание рядов методом наименьших квадратов по теоретическому уравнению регрессии y=a0 + a1x.
Для системы уравнений
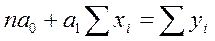 ,
,
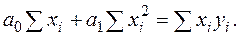
Метод наименьших квадратов применяется для определения параметров а0 и а1.
Смысл параметров:
а1 – это коэффициент регрессии, характеризующий влияние, которое оказывает изменение X на Y, т.е. объем выпущенной продукции на величину заработной платы, а1 показывает, на сколько единиц в среднем изменится Y при изменении X на единицу. Если а1> 0, то наблюдается положительная связь. Если а1< 0, то увеличение Х на единицу влечет за собой уменьшение Y в среднем на а1 (параметр а1 обладает размерностью отношения Y к Х).
Параметр а0 – это постоянная величина в уравнении регрессии, часто экономического смысла не имеет, но в ряде случаев ее интерпретируют как начальное значение Y.
Значение функции y=a0+a1х называется расчетным значением и на графике образует теоретическую линию регрессии. Смысл теоретической регрессии заключается в том, что это оценка среднего значения переменной Y для заданного значения Х.
Построить график теоретической прямой регрессии.
Этап 3. На основе полученного уравнения регрессии рассчитать значение корреляционного отношения и коэффициента детерминации и сделать вывод о степени связи между исследуемыми показателями.
Рассмотрим метод расчета коэффициента детерминации на основе уравнения парной линейной регрессии Ỹi=a0+a1·Xi. Анализ уравнения регрессии позволяет оценить роль исследуемого факторного признака в формировании результативного. Для этого необходимо определить долю фактора в общей изменчивости вариации результативного признака.
Рассмотрим метод разложения вариации по факторам.
Вариация любого показателя оценивается дисперсией. Для результата Y дисперсия s2носит название общей и обозначается s2общ (y):
s2общ (y)=М(у2)-[M(y)]2,
где М – математическое ожидание.
Далее для последовательной оценки вариации по сформированному уравнению регрессии нужно рассчитать теоретические значения результата. Обычно этот расчет оформляется в виде табл. 6.
Таблица 6
Расчет теоретических значений признака - результата
| Номер наблюдения | Значения Хi | Теоретические значения Ỹi=a0+a1·Xi | Ỹi2 |
| 1 | |||
| 2 | |||
| … | |||
| 20÷25 |
Далее оценивается так называемая факторная дисперсия
s2факт (Ỹ)=M(Ỹ2)-[M(Ỹ)]2.
Кроме представленного в данном уравнении регрессии фактора на конечный результат влияют другие факторы. Это влияние случайно. Дисперсию, вызываемую влиянием этих случайных факторов, называют остаточной:
s2ост (Y)= s2 общ (Y)- s2 факт (Ỹ).
Таким образом,
s2общ (Y)= s2факт (Ỹ)+ s2ост (Y).
Отношение 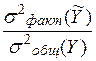 показывает долю факторной вариации в общей. Если это отношение равно 1, то результат Y полностью зависит только от влияния данного рассматриваемого фактора. Если это отношение равно 0, то данный результат зависит от случайных факторов.
показывает долю факторной вариации в общей. Если это отношение равно 1, то результат Y полностью зависит только от влияния данного рассматриваемого фактора. Если это отношение равно 0, то данный результат зависит от случайных факторов.
В экономическом анализе это отношение имеет особое значение и называется отношением детерминации:
η2= 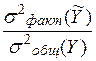 .
.
По нашим рассуждениям получаем
η2+ 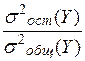 =1.
=1.
Отсюда получаем
η2=1- 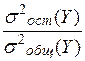 .
.
Это преобразование сделано для расчета так называемого коэффициента детерминации, который является универсальным показателем для оценки связи между исследуемыми признаками. Определяется он по формуле
η= 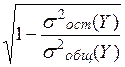 .
.
Границы изменения η от 0 до 1. Если η=1, то в наличии полная функциональная связь признака результата и признака фактора. Если η=0 – связь не обнаруживается. Коэффициент детерминации является универсальным потому, что он не зависит от вида связи между X и Y.
Лабораторная работа № 7
Дата: 2019-03-05, просмотров: 335.