Производная широко используется для исследования функций, т. е. для изучения различных свойств функций. Например, с помощью производных можно находить промежутки возрастания и убывания функции, ее наименьшие и наибольшие значения, точки максимума и минимума.
Пример. Построить график функции 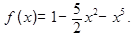
Решение .
1. Область определения — множество R всех действительных чисел.
2. 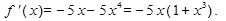
3. Решая уравнение 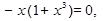 находим стационарные точки
находим стационарные точки 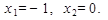
4. Производная положительная на интервале (-1;0), следовательно, на этом интервале функция возрастает. На промежутках 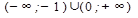 производная отрицательна, следовательно, на этих промежутках функция убывает.
производная отрицательна, следовательно, на этих промежутках функция убывает.
5. Стационарная точка 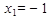 является точкой минимума, так как при переходе через эту точку производная меняет знак с «-» на «+»;
является точкой минимума, так как при переходе через эту точку производная меняет знак с «-» на «+»; 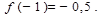 Точка
Точка 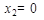 — точка максимума, так как при переходе через нее производная меняет знак с «+» на «-»;
— точка максимума, так как при переходе через нее производная меняет знак с «+» на «-»; 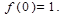
Использую результаты исследования, строим график функции.
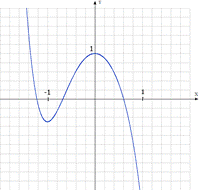
График функции построен с помощью исследования некоторых свойств этой функции. По графику можно выявить и другие свойства данной функции. Например, из рисунка видно, что уравнение 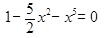 имеет три различных действительных корня.
имеет три различных действительных корня.
Фронтальная практическая работа
Построить график функции
1. 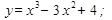 6.
6. 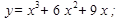
2. 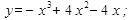 7.
7. 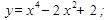
3. 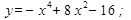 8.
8. 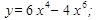
4. 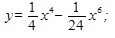 9.
9. 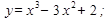
5. 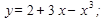 10.
10. 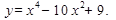
Практическая работа №15
Тема: Нахождение наибольшего, наименьшего значения и экстремальных значений функции.
Теоретические сведения к практической работе
Пусть функция 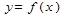 непрерывна на отрезке
непрерывна на отрезке 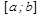 и имеет несколько критических точек на этом отрезке. Для нахождения наибольшего и наименьшего значений функции на данном отрезке нужно:
и имеет несколько критических точек на этом отрезке. Для нахождения наибольшего и наименьшего значений функции на данном отрезке нужно:
1. найти значения функции на концах отрезка, т. е. числа f ( a ) , f ( b ) ;
2. найти ее значения в тех критических точках, которые принадлежат интервалу ( a ; b ) ;
Из всех найденных значений выбрать наибольшее и наименьшее.
Пример 1. Функция 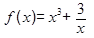 непрерывна на отрезке
непрерывна на отрезке 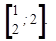 Найти ее наибольшее и наименьшее значения.
Найти ее наибольшее и наименьшее значения.
Решение .
1) 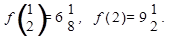
2) 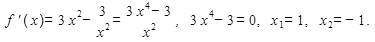
Интервалу 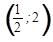 принадлежит одна стационарная точка
принадлежит одна стационарная точка 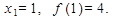
3) Из чисел 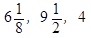 наибольшее
наибольшее 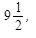 наименьшее 4.
наименьшее 4.
Пусть дана функция 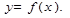 Для того, чтобы исследовать функцию на максимум и минимум необходимо придерживаться следующего алгоритма:
Для того, чтобы исследовать функцию на максимум и минимум необходимо придерживаться следующего алгоритма:
Найти производную функции.
Найти критические точки функции, т. е. точки, в которых производная обращается в нуль или терпит разрыв.
3. Исследовать знак производной в промежутках, на которые найденные критические точки делят область определения функции. При этом критическая точка есть точка минимума, если производная меняет знак с «минуса» на «плюс» при переходе через эту точку, иначе точка максимума.
Дата: 2019-03-05, просмотров: 543.