Классическое определение вероятности

       Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению данного события А, к числу n всех исходов (несовместных, единственно возможных и равновозможных), т. е.

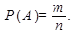
Пример 1. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?

Решение. Общее число различных исходов есть n =1000. Число исходов, благоприятствующих получению выигрыша, составляет m =200. Согласно определению, получим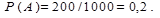

Пример 2. Из урны, в которой находятся 12 белых и 8 черных шаров, вынимают наудачу два шара. Какова вероятность того, что оба шара окажутся черными?

Решение. Обозначим событие, состоящее в появлении двух черных шаров, через А. Общее число возможных случаев n равно числу сочетаний из (12+8) элементов по два. Тогда

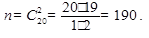
Число случаев m, благоприятствующих событию А, составляет

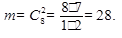
По определению находим вероятность появления двух черных шаров

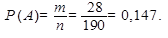
       Теоремы сложения вероятностей.

       Теорема сложения вероятностей несовместных событий

       Вероятность одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

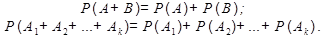
       Теорема сложения вероятностей совместных событий

       Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

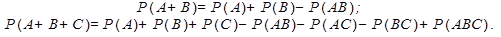
Пример 3. В ящике в случайном порядке разложены 20 деталей, причем пять из них стандартные. Рабочий берет наудачу три детали. Найти вероятность того, что по крайней мере одна из взятых деталей окажется стандартной (событие А).

Решение. По крайней мере одна из взятых деталей окажется стандартной, если произойдет любое из трех несовместных событий: В — одна деталь стандартная, две нестандартные; С — две детали стандартные, одна не стандартная и D — три детали стандартные.

       Таким образом, событие А можно представить в виде суммы этих трех событий: A = B + C + D. По теореме сложения имеем P ( A )= P ( B )+ P ( C )+ P ( D ). Находим вероятность каждого из этих событий:

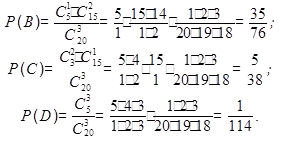
Сложив найденные величины, получим P ( A )=0,601.

Пример 4. Найти вероятность того, что наудачу взятое двузначное число кратно 3, либо 5, либо тому и другому одновременно.

Решение. Пусть А — событие, состоящее в том, что наудачу взятое число кратно 3, а В — в том, что оно кратно 5. Найдем Р(А+В). Так как А и В совместные события, то воспользуемся теоремой сложения вероятностей совместных событий.

       Всего 90 двузначных чисел. Из них 30 являются кратными 3; 18 кратными 5 и 6 — кратными одновременно 3 и 5. Таким образом, 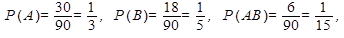т. е. Р(А+В)=0,467.