Физический смысл производной заключается в том, что производная выражает скорость протекания процесса, описываемого зависимостью 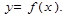
Пример 1. Материальная точка движется прямолинейно по закону 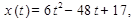 где x - расстояние от точки отсчета в метрах, t - время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9с.
где x - расстояние от точки отсчета в метрах, t - время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9с.
Решение. Производная функции х(t): 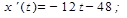
подставляем в производную значение момента времени t=9с., тогда x'(9)=60. Таким образом, скорость точки в момент t=9 с составит 60 м/с.
Геометрический смысл производной заключается в том, что производная функции 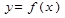 в точке А равна угловому коэффициенту касательной, проведенной к графику функции в этой точке и равна тангенсу угла наклона касательной.
в точке А равна угловому коэффициенту касательной, проведенной к графику функции в этой точке и равна тангенсу угла наклона касательной.
Пример 2. Найти угол наклона параболы 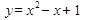 к оси Ох в точке
к оси Ох в точке 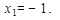
Решение. Для вычисления угла наклона кривой найдем производную функции в данной точке:
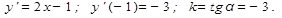 По таблице определяем
По таблице определяем 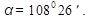
Фронтальная практическая работа
1. Точка движется по закону 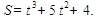 Найдите величины скорости в момент времени
Найдите величины скорости в момент времени 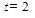 c.
c.
2. Точка движется прямолинейно по закону 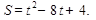 В какой момент времени
В какой момент времени 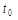 скорость точки окажется равной нулю?
скорость точки окажется равной нулю?
3. Тело массой m=12 кг движется прямолинейно по закону 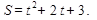 Найдите кинетическую энергию тела через 5 с после начала движения.
Найдите кинетическую энергию тела через 5 с после начала движения.
4. Зависимость температуры тела Т от времени t задана уравнением 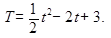 С какой скоростью нагревается это тело в момент времени t=10с?
С какой скоростью нагревается это тело в момент времени t=10с?
5. Сила тока изменяется в зависимости от времени по закону 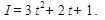 Найдите скорость изменения силы тока через 8 с.
Найдите скорость изменения силы тока через 8 с.
6. Найдите угловой коэффициент касательной, проведенной к параболе 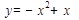 в точке
в точке 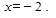
7. Найдите угол наклона параболы 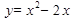 к оси Ох в точке х=2.
к оси Ох в точке х=2.
Практическая работа №13
Тема: Уравнение касательной в общем виде.
Теоретические сведения к практической работе
Геометрический смысл производной состоит в том, что значение производной функции 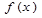 в точке х равно угловому коэффициенту касательной к графику функции в точке
в точке х равно угловому коэффициенту касательной к графику функции в точке 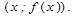
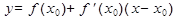 — уравнение касательной к графику дифференцируемой функции в точке
— уравнение касательной к графику дифференцируемой функции в точке 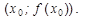
Пример 1. Найти уравнение касательной к графику функции 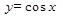 в точке с абсциссой
в точке с абсциссой 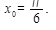
Решение . Найдем значения функции 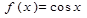 и ее производной в точке
и ее производной в точке 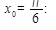
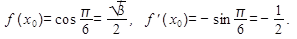 Используя формулу, найдем уравнение касательной:
Используя формулу, найдем уравнение касательной: 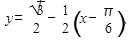 или
или 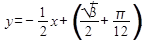
Пример 2. Показать, что касательная к параболе 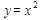 в точке с абсциссой х0 пересекает ось Ох в точке
в точке с абсциссой х0 пересекает ось Ох в точке 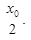
Решение . Пусть 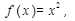 тогда
тогда 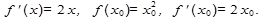
По формуле найдем уравнение касательной: 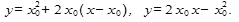
Найдем точку пересечения этой касательной с осью абсцисс. Из равенства 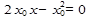 находим
находим 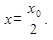
Фронтальная практическая работа
Написать уравнение касательной к графику функции 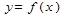 в точке с абсциссой х0:
в точке с абсциссой х0:
1. 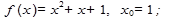 6.
6. 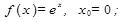
2. 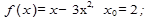 7.
7. 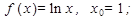
3. 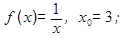 8.
8. 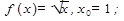
4. 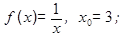 9.
9. 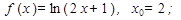
5. 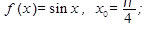 10.
10. 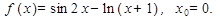
Практическая работа №14
Тема: Исследование функции с помощью производной.
Дата: 2019-03-05, просмотров: 438.