(Описание решений для задания № 3 к контрольной работе)
Рассмотрим решение транспортной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (таблица 3.4).
Задача 2.
Таблица 3.4
Исходные данные транспортной задачи
| Тарифы, грн. шт. | 1-й магазин | 2-й магазин | 3-й магазин | Запасы, шт. |
| 1-й склад | 2 | 9 | 7 | 25 |
| 2-й склад | 1 | 0 | 5 | 50 |
| 3-й склад | 5 | 4 | 100 | 35 |
| 4-й склад | 2 | 3 | 6 | 75 |
| Потребности шт. | 45 | 90 | 50 |
Целевая функция и ограничения данной задачи имеют вид
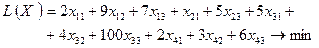
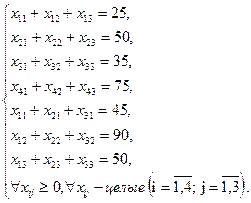(3.13)
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий транспортной задачи (3.13) и ее решение представлены на рисунках 3.1, 3.2, 3.3 и в таблице 3.4
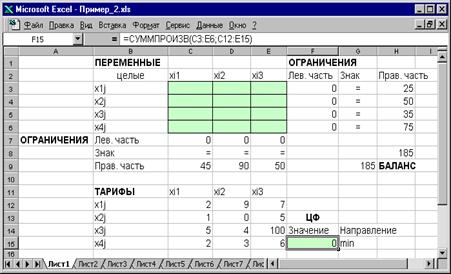
Рисунок 3.1 Экранная форма транспортной задачи 2 (курсор в целевой ячейке F 15)
Таблица 3.5.
Формулы экранной формы задачи (1.5)
| Объект математической модели | Выражение в Excel |
| Переменные задачи | C3:E6 |
| Формула в целевой ячейке F15 | =СУММПРОИЗВ(C3:E6;C12:E15) |
| Ограничения по строкам в ячейках F3, F4, F5, F6 | =СУММ(C3:E3) =СУММ(C4:E4) =СУММ(C5:E5) =СУММ(C6:E6) |
| Ограничения по столбцам в ячейках С7, D7, E7 | =СУММ(C3:C6) =СУММ(D3:D6) =СУММ(E3:E6) |
| Суммарные запасы и потребности в ячейках H8, G9 | =СУММ(H3:H6) =СУММ( C 9: E 9) |
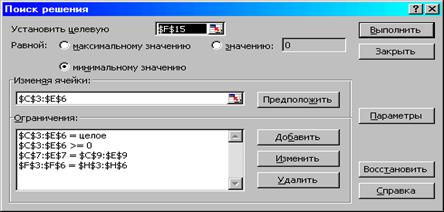
Рисунок 3.2. Ограничения и граничные условия задачи 2
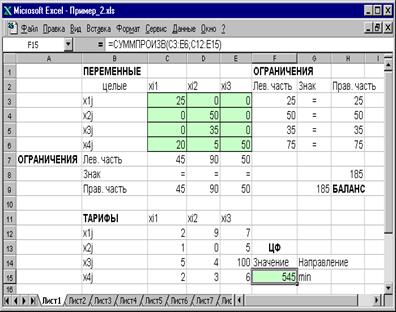
Рисунок 3.3. Экранная форма после получения решения задачи (1.5) (курсор в целевой ячейке F 15)
Задание к контрольной работе № 3.
Используя MS Excel, найти решение транспортной задачи, соответствующей заданному варианту.
Вариант № 1.
| ai \ вj | 700 | 300 | 200 | 400 |
| 900 | 18 | 20 | 14 | 10 |
| 300 | 10 | 20 | 30 | 30 |
| 400 | 16 | 22 | 10 | 20 |
Вариант № 2.
| ai \ вj | 60 | 65 | 75 | 50 |
| 70 | 0 | 4 | 3 | 1 |
| 80 | 4 | 3 | 2 | 2 |
| 80 | 6 | 3 | 5 | 5 |
| 20 | 4 | 7 | 6 | 1 |
Вариант № 3.
| ai \ вj | 100 | 400 | 200 | 300 |
| 100 | 2 | 4 | 2 | 1 |
| 150 | 3 | 1 | 5 | 6 |
| 250 | 1 | 7 | 3 | 5 |
| 500 | 5 | 8 | 6 | 1 |
Вариант № 4.
| ai \ вj | 400 | 200 | 200 | 200 |
| 250 | 6 | 1 | 4 | 2 |
| 300 | 3 | 5 | 1 | 3 |
| 350 | 5 | 6 | 7 | 1 |
| 100 | 2 | 1 | 8 | 5 |
Вариант № 5.
| ai \ вj | 30 | 70 | 50 | 100 |
| 70 | 7 | 5 | 1 | 6 |
| 120 | 5 | 3 | 4 | 9 |
| 20 | 6 | 8 | 7 | 7 |
| 40 | 4 | 3 | 5 | 5 |
Вариант № 6.
| ai \ вj | 75 | 125 | 60 | 140 |
| 80 | 4 | 5 | 2 | 10 |
| 40 | 7 | 3 | 2 | 4 |
| 160 | 3 | 4 | 3 | 5 |
| 120 | 5 | 7 | 9 | 6 |
Вариант № 7.
| ai \ вj | 450 | 400 | 50 | 140 |
| 300 | 7 | 9 | 9 | 5 |
| 150 | 2 | 5 | 8 | 9 |
| 350 | 5 | 6 | 4 | 8 |
| 200 | 3 | 11 | 2 | 3 |
Вариант № 8.
| ai \ вj | 25 | 35 | 45 | 35 |
| 50 | 6 | 8 | 2 | 4 |
| 30 | 7 | 2 | 5 | 4 |
| 40 | 8 | 1 | 7 | 2 |
| 20 | 1 | 2 | 8 | 10 |
Вариант № 9.
| ai \ вj | 60 | 40 | 35 | 65 |
| 45 | 4 | 2 | 3 | 2 |
| 30 | 7 | 5 | 7 | 3 |
| 50 | 2 | 6 | 8 | 4 |
| 75 | 5 | 1 | 3 | 1 |
Вариант № 10.
| ai \ вj | 200 | 100 | 80 | 120 |
| 60 | 2 | 5 | 4 | 2 |
| 140 | 3 | 1 | 3 | 1 |
| 160 | 6 | 3 | 3 | 2 |
| 140 | 3 | 4 | 6 | 0 |
Вариант № 11.
| ai \ вj | 600 | 400 | 200 |
| 100 | 6 | 15 | 9 |
| 400 | 7 | 10 | 16 |
| 700 | 9 | 11 | 15 |
Вариант № 12.
| ai \ вj | 40 | 120 | 40 | 20 |
| 150 | 1 | 1 | 3 | 2 |
| 50 | 4 | 8 | 4 | 3 |
| 20 | 3 | 3 | 2 | 2 |
Вариант № 13.
| ai \ вj | 250 | 250 | 400 | 600 |
| 350 | 8 | 1 | 10 | 8 |
| 650 | 11 | 15 | 11 | 7 |
| 500 | 12 | 7 | 15 | 12 |
Вариант № 14.
| ai \ вj | 700 | 300 | 200 | 400 |
| 900 | 18 | 20 | 14 | 10 |
| 300 | 10 | 20 | 30 | 30 |
| 400 | 16 | 22 | 10 | 20 |
Вариант № 15.
| ai \ вj | 100 | 100 | 400 | 1000 |
| 500 | 20 | 10 | 30 | 50 |
| 800 | 30 | 20 | 30 | 20 |
| 300 | 30 | 50 | 50 | 50 |
Вариант № 16.
| ai \ вj | 450 | 350 | 550 | 650 |
| 500 | 4 | 1 | 3 | 5 |
| 600 | 2 | 2 | 3 | 7 |
| 900 | 4 | 3 | 5 | 3 |
Список используемой литературы
1. Костевич Л.С. Математическое программирование: Информ. технологии оптимальных решений. – Мн.: Новое знание, 2003. – 424 с.
2. Дорохина Е.Ю., Халиков М.А. Моделирование микроэкономики. учебное пособие для вузов/ под общ. ред. Н.П. Тихомирова – М.:Издательство «Экзамен», 2003. – 224 с.
3. Замков О.О., Толстопятенко А.В.,Черемных Ю.Н Математические методы в экономике: Учебник МГУ им. М,В. Ломоносова. М.: ДИС, 2000.- 346 с.
4. Интрилигатор М. Математические методы оптимизации и экономическая теории. М.: Прогресс, 2001. – 300 с.
5. Нейман Дж., Моргенштерн О. Теория игр и экономическое моделирование. М.: Наука, 2003. – 206 с.
Дата: 2019-03-05, просмотров: 405.
