МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ»
Факультет «Экономика, управление и информационные системы в строительстве и недвижимости
Кафедра «Менеджмент строительных организаций»
А.О. Коломыцева
Математические методы и модели в экономике и менеджменте.
Реализация в MS Excel
Учебно-методические материалы к организации самостоятельной работы студентов и выполнения контрольной работы студентов заочной формы обучения
Макеевка 2018
Содержание
Введение 4
Оптимизационные модели производства и распределения ресурсов 5
1.1. Понятие экономико-математической модели 5
1.2. Задача на максимум дохода 7
1.3. Задача на минимум затрат 11
1.4. Решение задач линейного программирования (ЛП) с помощью MS Excel 19
1.5. Задание к контрольной работе № 1. 21
2. Оптимизационные целочисленные модели 26
2.1. Вариантная производственная задача 26
2.2. Решение целочисленных задач линейного программирования (ЛП) с помощью MS Excel 28
2.3. Решение задач линейного программирования (ЛП) с булевыми переменными с помощью MS Excel 29
2.4. Задание к контрольной работе № 2. 31
3. Построение и анализ транспорно-производственных моделей 31
3.1. Модификация транспортной задачи 31
3.2. Решение транспортной задачи с помощью MS Excel 34
3.3. Задание к контрольной работе № 3. 37
Список используемой литературы 39
Введение
Моделирование – специфический научный метод, применяемый для анализа и синтеза систем управления. Это особенный познавательный способ, когда субъект исследования вместо непосредственного исследования объекта познания выбирает или создает подобный ему вспомогательный объект – образ или модель, исследует его, а полученные новые знания переносит на объект-оригинал.
При построении модели с использованием электронных таблиц, во-первых, не теряется алгоритм решения задачи, во-вторых, студент освобождается от рутинной работы расчетов, и в-третьих, студент обучается в совершенстве владеть электронными таблицами.
Широкое использование информационных технологий в значительной степени интенсифицирует процесс освоения методики построения моделей.
Цель подготовки учебного пособия – дать взаимосвязанное и достаточно полное описание основных теоретико-методологических принципов и методических подходов к постановке, моделированию, решению и анализу экономических задач в сфере микроэкономики на основе экономико-математических методов.
Оптимизационные модели производства и распределения ресурсов в экономике и менеджменте
(описание теоретического материала по дисциплине необходимого для подготовки к выполнению заданий контрольной работы 1, примеры выполнения которой приведены ниже)
Задача на минимум затрат
Введем новое обозначение: 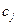 - себестоимость единицы j-й продукции.
- себестоимость единицы j-й продукции.
Запишем простую модель с критерием оптимальности - минимум затрат на весь объем выпуска:
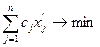 ;
;
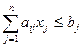
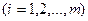
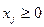
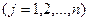 .
.
Поиск оптимального решения в этом случае очень прост - им является тривиальное (все неизвестные равны нулю) решение. Действительно, при 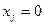
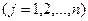 все ограничении выполняются, т.е. данное решение допустима A из вcex допустимых решений оно дает наименьшее значение критерия оптимальности, т.е. затраты в данном случае равны нулю (очевидно, что отрицательными они быть не мoгyт).
все ограничении выполняются, т.е. данное решение допустима A из вcex допустимых решений оно дает наименьшее значение критерия оптимальности, т.е. затраты в данном случае равны нулю (очевидно, что отрицательными они быть не мoгyт).
Такое математически правильное решение с экономической точки зрения абсурдно, ибо представляет собой план «максимальной экономии ресурсов», в соответствии с которым ничего не производится и все ресурсы остаются целиком неиспользованными.
Ничего не изменит и запись модели, усложненная за счет введении различных технологических способов производства одноименной продукции, где 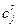 - себестоимость единицы продукции j-гo вида, произведенной по s-му способу.
- себестоимость единицы продукции j-гo вида, произведенной по s-му способу.
Чтобы значение критерия оптимальности не «скатывалось» до нуля, необходимо ограничит снизу (т.е. ввести ограничение вида 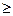 ) решение. Такими условиями, как мы уже знаем, являются условия по выполнению директивно заданного плана производства.
) решение. Такими условиями, как мы уже знаем, являются условия по выполнению директивно заданного плана производства.
Экономическая деятельность, как одна из видов человеческой, целенаправленна и предполагает достижение определенных результатов производства, что, и в свою очередь, связано с осуществлением затрат. Одной из основных задач экономики (как науки, так и практики) является сопоставление затрат и результатов. Как правило, существует несколько вариантов получении заранее заданною (планируемого, желаемого, предполагаемого, фиксированного) результата. Также существует несколько вариантов использования известного (имеющегося), фиксированного количества ресурсом. Правильный выбор наилучшею варианта из нескольких допустимых возможен при следующих постановках задачи:
- максимизация результата (эффекта) при фиксированном уровне затрат (ресурсов);
- минимизация затрат при фиксированном уровне результатов.
Сам отбор наилучшего варианта решения (плана производства) по минимуму затрат возможен вследствие эквивалентности результатов по всем вариантам. В случае же различной величины результатов вариант с меньшими затратами может и не быть лучшим (просто с меньшими затратами мы достигаем и меньшего результата). Именно это имело место выше. «Лучшее», нулевое решение давало наименьший (выпуск равен нулю) результат.
Рассмотрим модель задачи на минимум затрат при фиксированных планах производства, предположив, что каждый вид продукции производится лишь одним технологическим способом:
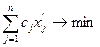
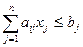
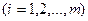 ;
;
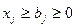
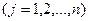 .
.
Любой сверхплановый выпуск, даже самых скромных размеров, увеличит значение критерия оптимальности. Ясно, что наименьший уровень затрат возможен лишь при строгом выполнении плановых заданий, т.е. при 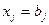 . Тем самым данная модель теряет смысл, так как в подобной задаче нечего искать. Оптимальный план известен: он задается числами
. Тем самым данная модель теряет смысл, так как в подобной задаче нечего искать. Оптимальный план известен: он задается числами 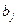 .
.
Однако это не значит, что при отсутствии нескольких способов производства одноименной продукции постановка задачи на минимум затрат бессмысленна. Нужно лишь задать peзультат с меньшей, степенью подробности, нежели искомые величины:
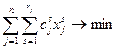 ; (1.16)
; (1.16)
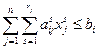
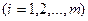 ; (1.17)
; (1.17)
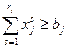
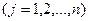 ; (1.18)
; (1.18)
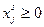
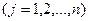
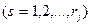 (1.19)
(1.19)
В модели (1.16)-(1.19) переменные 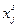 детализированы и по видам продукции j и по способам производства s, а плановые задания
детализированы и по видам продукции j и по способам производства s, а плановые задания 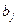 - лишь по продукции. Поэтому оптимизация осуществляется подбором разных величин
- лишь по продукции. Поэтому оптимизация осуществляется подбором разных величин 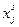 в рамках единой фиксированной величины
в рамках единой фиксированной величины 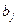 , т.e. подбором сочетания различных технологий для выпуска данной j-й продукции.
, т.e. подбором сочетания различных технологий для выпуска данной j-й продукции.
Рассмотрим еще один подход, позволяющий ограничить решение в задаче на минимум затрат снизу. Обозначим в данном случае через 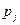 цены на продукцию j-ro вида, а через Р - план по валовой продукции. Заменим детальные ограничения
цены на продукцию j-ro вида, а через Р - план по валовой продукции. Заменим детальные ограничения 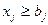 aгpегированным ограничением
aгpегированным ограничением 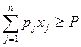 (если вернутся к первоначальному определению величии
(если вернутся к первоначальному определению величии 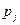 , то Р будет не чем иным, как запланированным уровнем валового дохода от выпуска продукции)
, то Р будет не чем иным, как запланированным уровнем валового дохода от выпуска продукции)
Тогда модель на минимум затрат в случае, когда каждый вид продукта производится лишь одним технологическим способом, запишется так

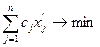 ; (1.20)
; (1.20)
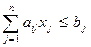
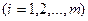 ; (1.21)
; (1.21)
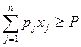 ; (1.22)
; (1.22)
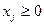
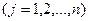 . (1.23)
. (1.23)
Отметим одну важную особенность рассмотренных моделей (1.16)-(1.19) и (1 20)-(1.23). Ограничения на область допустимых решений (1.17)-(1.18) и (1.21)-(1.22) в принципе противоречивы: ограничения вида « 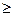 » по объему производства или валовому доходу могут потребовать расхода одного или нескольких ресурсов, превышающего их наличный зaпаc, учитываемый в ограничениях вида «
» по объему производства или валовому доходу могут потребовать расхода одного или нескольких ресурсов, превышающего их наличный зaпаc, учитываемый в ограничениях вида « 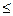 ».
».
Противоречивость рассматриваемых ограничений при решении задачи с конкретными значениями 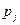 и
и 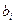 может привести к тому, что область допустимых решений окажется пустой и оптимизационная задача будет неразрешимой.
может привести к тому, что область допустимых решений окажется пустой и оптимизационная задача будет неразрешимой.
Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода задачи 1 вместе с введенными в нее исходными данными представлена на рисунок 1.1.
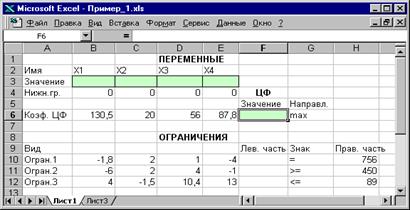
Рисунок 1.1. Экранная форма задачи 1 (курсор в ячейке F6)
В экранной форме на рис.1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи (1.1) соответствуют ячейки B3 ( 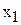 ), C3 (
), C3 ( 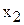 ), D3 (
), D3 ( 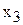 ), E3 (
), E3 ( 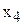 ), коэффициентам ЦФ соответствуют ячейки B6 (
), коэффициентам ЦФ соответствуют ячейки B6 ( 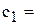 130,5), C6 (
130,5), C6 ( 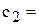 20), D6 (
20), D6 ( 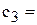 56), E6 (
56), E6 ( 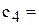 87,8), правым частям ограничений соответствуют ячейки H 10 (
87,8), правым частям ограничений соответствуют ячейки H 10 ( 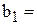 756), H 11 (
756), H 11 ( 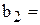 450), H 12 (
450), H 12 ( 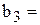 89) и т.д.
89) и т.д.
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку F 6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
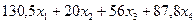 (1.25)
(1.25)
Используя обозначения соответствующих ячеек в Excel (см. рисунок 1.1), формулу для расчета ЦФ (1.25) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B6, C6, D6, E6), то есть
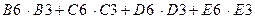 (1.26)
(1.26)
Чтобы задать формулу (1.3) необходимо в ячейку F 6 ввести следующее выражение и нажать клавишу " Enter "
=СУММПРОИЗВ( B$3: E$3; B6: E6), (1.27)
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись B6:E6 указывает на ячейки B6, C6, D6 и E6). После этого в целевой ячейке появится 0 (нулевое значение) (рисунок 1.2).
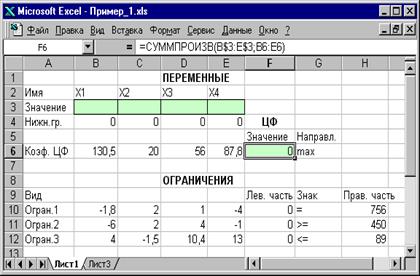
Рисунок 1.2. Экранная форма задачи 1 после ввода всех необходимых формул (курсор в ячейке F6)
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима "Вставка функций", который можно вызвать из меню "Вставка" или при нажатии кнопки "  " на стандартной панели инструментов. Так, например, формулу (1.27) можно задать следующим образом:
" на стандартной панели инструментов. Так, например, формулу (1.27) можно задать следующим образом:
· курсор в поле F 6;
· нажав кнопку "  ", вызовите окно "Мастер функций – шаг 1 из 2";
", вызовите окно "Мастер функций – шаг 1 из 2";
· выберите в окне "Категория" категорию "Математические";
· в окне "Функция" выберите функцию СУММПРОИЗВ;
· в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B $3: E $3, а в строку "Массив 2" – выражение B 6: E 6 (рис.1.3);
· после ввода ячеек в строки "Массив 1" и "Массив 2" в окне "СУММПРОИЗВ" появятся числовые значения введенных массивов (см. рис.1.3), а в экранной форме в ячейке F 6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
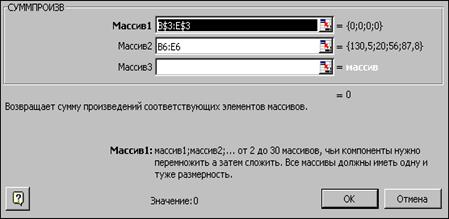
Рисунок 1.3. Ввод формулы для расчета ЦФ в окно "Мастер функций"
Зависимости для левых частей ограничений
Левые части ограничений задачи 1 представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10, D10, E10 – 1-е ограничение; B11, C11, D11, E11 – 2-е ограничение и B12, C12, D12, E12 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в таблице 1.2.
Таблица 1.2
Формулы, описывающие ограничения модели 1.
| Левая часть ограничения | Формула Excel |
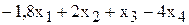 или или
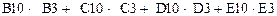
| =СУММПРОИЗВ (B$3:E$3;B10:E10) |
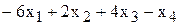 или или
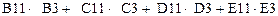
| =СУММПРОИЗВ (B$3:E$3;B11:E11) |
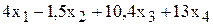 или или
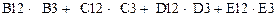
| =СУММПРОИЗВ (B$3:E$3;B12:E12) |
Как видно из таблицы 1.1, формулы, задающие левые части ограничений задачи 1, отличаются друг от друга и от формулы (1.27) в целевой ячейке F 6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:
· поместить курсор в поле целевой ячейки F 6 и скопировать в буфер содержимое ячейки F 6 (клавишами " Ctrl - Insert ");
· помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F 10, F 11 и F 12, и вставлять в эти поля содержимое буфера (клавишами " Shift - Insert ") (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);
· на экране в полях F 10, F 11 и F 12 появится 0 (нулевое значение) (см. рисунок 1.2).
Запуск задачи на решение
Запуск задачи на решение производится из окна "Поиск решения" путем нажатия кнопки "Выполнить".
После запуска на решение задачи ЛП на экране появляется окно "Результаты поиска решения" с одним из сообщений, представленных на рисунках 1.9, 1.10 и 1.11.
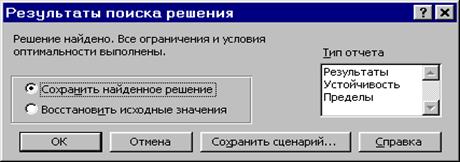
Рисунок 1.9. Сообщение об успешном решении задачи
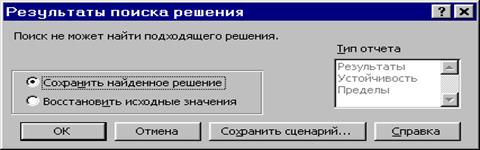
Рисунок 1.10. Сообщение при несовместной системе ограничений задачи
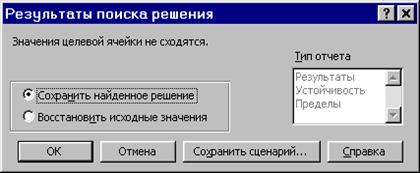
Рисунок 1.11. Сообщение при неограниченности ЦФ в требуемом направлении
Иногда сообщения, представленные на рис.1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна "Поиск решения" были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра "Относительная погрешность" не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне "Результаты поиска решения" представлены названия трех типов отчетов: "Результаты", "Устойчивость", "Пределы". Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку "OK". После этого в экранной форме появляется оптимальное решение задачи (рисунок 1.12).
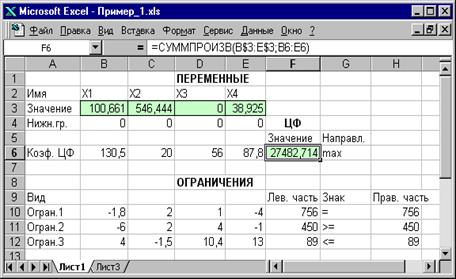
Рисунок 1.12. Экранная форма задачи 1 после получения решения
Задание к контрольной работе № 1.
Используя MS Excel, найти решение для модели ЛП, соответствующей заданному варианту.
Вариант № 1.
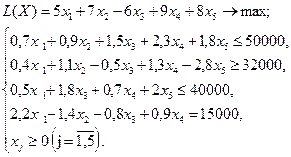
Вариант № 2
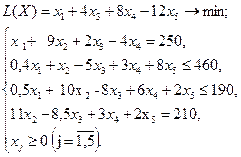
Вариант № 3
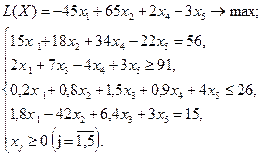
Вариант № 4
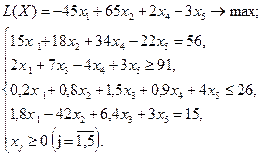
Вариант № 5
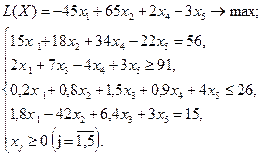
Вариант № 6
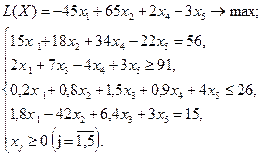
Вариант № 7
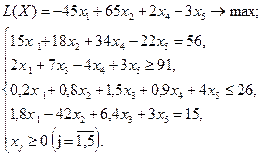
Вариант № 8
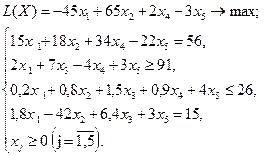
Вариант № 9
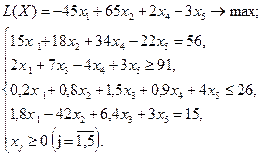
Вариант № 10
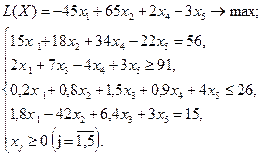
Вариант № 11
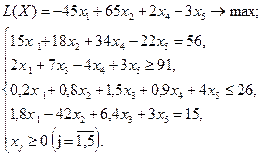
Вариант № 12
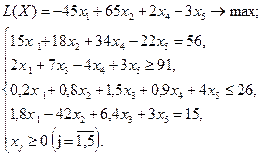
Вариант № 13
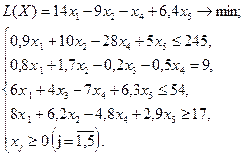
Вариант № 14
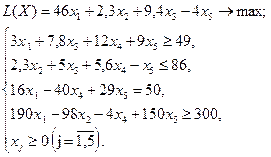
Вариант № 15
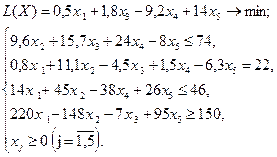
Вариант № 16
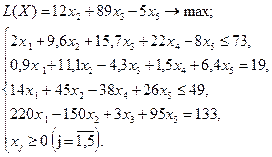
Вариантная производственная задача
Рассмотрим одну из целочисленных моделей. Предельный проявлением целочисленности является использование в модели булевых переменных - единицы и нули. Логически –это соответствует выбору между «да» и «нет». Это, в свою очередь, требует заранее сформулировать те варианты производственной программы, варианты развития экономического поведения, которые и будут в дальнейшем подвергнуты анализу и отбору. Таким образом, содержание задачи в данном случае состоит в следующим: принять или отвергнуть варианты из их заранее известного сформированною набора. Причем целиком принять или целиком отвергнуть (частичные решения запрещены) каждый из них. Соответствуюшую модель принято называть вариантной, ибо она построена на основании заранее известныx заданных вариантов и ее содержание будет ивляться сортировка таких вариантов на эффективные, принятые в оптимальный план, и неэффективные , т.е. отвергнутые.
Введем следующие oбозначения:
i - индекс ресурсов 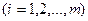 ;
;
j - индекс продукции 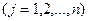 ;
;
k - индекс предприятия, входящего в данное объединение, фирму 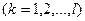 ;
;
r - индекс варианта плана производства на k-м предприятии 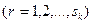 ;
;
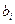 - наличный объем i-го ресурса;
- наличный объем i-го ресурса;
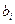 - план выпуска j-ой продукции;
- план выпуска j-ой продукции;
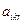 - общий объем потребления i-го ресурса на k-м предприятии при его работе целиком по r-му варианту;
- общий объем потребления i-го ресурса на k-м предприятии при его работе целиком по r-му варианту;
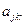 - общие размеры выпуска j-й продукции на k-м предприятии при его работе целиком по r-му варианту;
- общие размеры выпуска j-й продукции на k-м предприятии при его работе целиком по r-му варианту;
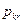 - общее количество прибыли k-го предприятия при его работе целиком по r-му варианту;
- общее количество прибыли k-го предприятия при его работе целиком по r-му варианту;
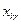 - булевая переменная принятая или не принятая.
- булевая переменная принятая или не принятая.
Таким образом, набор известных величин 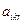 ,
, 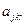 и
и 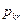 однозначно определит любой из вариантов на каждом предприятии. Следует, подчеркнуть, что в отличие от предыдущих моделей, величины
однозначно определит любой из вариантов на каждом предприятии. Следует, подчеркнуть, что в отличие от предыдущих моделей, величины 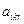 ,
, 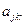 и
и 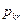 не являются удельными величинами. Они характеризуют расход ресурсов, выпуск продукции и прибыль при реализации на k-м предприятии r-го варианта в полном его объеме. Кроме того, сразу оговорим, что критерием оптимальности может быть не обязательно максимум прибыли, а любой из рассмотренных выше.
не являются удельными величинами. Они характеризуют расход ресурсов, выпуск продукции и прибыль при реализации на k-м предприятии r-го варианта в полном его объеме. Кроме того, сразу оговорим, что критерием оптимальности может быть не обязательно максимум прибыли, а любой из рассмотренных выше.
В принятых обозначениях модель вариантной производственной задачи запишется следующим образом.
Найти значения переменных. 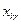 максимизирующих целевую функцию вида
максимизирующих целевую функцию вида
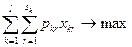 (2.1)
(2.1)
(т.е. максимизировать совокупный объем прибыли всего объединения, фирмы) при выполнении ограничений на использование ресурсов
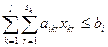
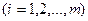 ; (2.2)
; (2.2)
по выполнению производственной программы
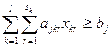
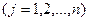 ; (2.3)
; (2.3)
по выбору вариантов
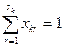
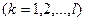 ; (2.4)
; (2.4)
и целочисленности переменных
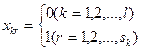 . (2.5)
. (2.5)
Ограничения вида (2.5) показывает, что интенсивность использования любого из вариантов может принимать лишь два значения соответственно которым он может быть либо принят (в случае 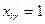 ), либо отвергнуть (в случае
), либо отвергнуть (в случае 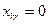 ). Ограничения вида (2.4) обеспечиваю на каждом предприятии выбор только одного из всех возможных на нем вариантов. Левая часть должна представлять собой сумму одной единицы: и нулей, иначе равенство в (2.4) нарушится. Таким образом, на одном предприятии нельзя выбрать как cpaзу несколько вариантов, так и ни иного. В левой части ограничений (2.2) и (2.3) каждое предприятие фактически будет представлено не суммарным по всем вариантам использованием ресурсов и выпуском продукции, а лишь теми показателями, которые описывание использование ресурсов и выпуск продукции по выбранному варианту работы данного предприятия. В силу (2.4) и (2.5)
). Ограничения вида (2.4) обеспечиваю на каждом предприятии выбор только одного из всех возможных на нем вариантов. Левая часть должна представлять собой сумму одной единицы: и нулей, иначе равенство в (2.4) нарушится. Таким образом, на одном предприятии нельзя выбрать как cpaзу несколько вариантов, так и ни иного. В левой части ограничений (2.2) и (2.3) каждое предприятие фактически будет представлено не суммарным по всем вариантам использованием ресурсов и выпуском продукции, а лишь теми показателями, которые описывание использование ресурсов и выпуск продукции по выбранному варианту работы данного предприятия. В силу (2.4) и (2.5)
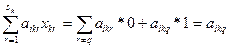
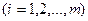 ;
;
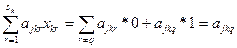
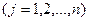 .
.
где 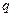 индекс того варианта работы k-го предприятия, который вошел в план (не обязательно оптимальный, но допустимый) и для которого
индекс того варианта работы k-го предприятия, который вошел в план (не обязательно оптимальный, но допустимый) и для которого 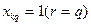 . Таким oбpaзом, все прочие отвергнутые варианты как бы пропадают и не участвуют как в использовании ресурсов, так и в выпуске продукции. Аналогично и общая прибыль по объединению, фирме будет фактически формироваться включительно как сумма прибыли, oт вошедших в план вариантов.
. Таким oбpaзом, все прочие отвергнутые варианты как бы пропадают и не участвуют как в использовании ресурсов, так и в выпуске продукции. Аналогично и общая прибыль по объединению, фирме будет фактически формироваться включительно как сумма прибыли, oт вошедших в план вариантов.
Условие (2.4) может быть сформулировано и менее жестко, если предположить, что для каждого предприятия (в случае его меньшей выгодности по сравнению с другими) могут быть, отвергнуты все предложенные варианты. Здесь мы будем иметь случай уже не только отбора того или иного варианта на предприятии, но и отбора среди самих предприятий, сортировки их на эффективные, вошедшие в план, и неэффективные, отвергнутые. Для такой ситуации ограничения вида (2.4) будут модифицированы следующим образом:
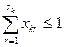
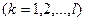 (2.6)
(2.6)
Зачастую возникает и промежуточная ситуация, когда для части предприятий выбор одною из возможных вариантов обязателен. Введем обозначения:
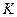 - множество индексов предприятий
- множество индексов предприятий 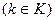 ;
;
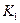 - множество индексов предприятий, участие которых в плане не обязательно, т.е. которые могут быть закрыты, перепрофилированы и т.д.
- множество индексов предприятий, участие которых в плане не обязательно, т.е. которые могут быть закрыты, перепрофилированы и т.д. 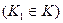 ;
;
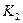 - множество индексов предприятий, участие которых в плане обязательно, т.е. не подлежащих -закрытию, перепрофилированию и т.п.
- множество индексов предприятий, участие которых в плане обязательно, т.е. не подлежащих -закрытию, перепрофилированию и т.п. 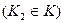 .
.
С учетом этих обозначений вместо ограничений вида (2.4) в модели вариантной задачи появятся ограничения двух видов:
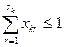
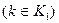 ; (2.7)
; (2.7)
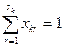
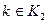 . (2.8)
. (2.8)
В ограничениях вида (2.8) допускаются нулевые значения всех 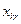 ,а следовательно, и нулевые значения, левой части в целом. Это будет свидетельствовать о невыгодности ни одного из вариантов работы данного предприятия, а следовательно, и о его невыгодности в целом. Выполнение условия (2.7) как строгого неравенства может свидетельствовать либо о целесообразности закрытия, перепрофилирования соответствующего предприятия, либо о недостаточном качестве набора вариантов и необходимости нахождения для него более эффективных вариантов.
,а следовательно, и нулевые значения, левой части в целом. Это будет свидетельствовать о невыгодности ни одного из вариантов работы данного предприятия, а следовательно, и о его невыгодности в целом. Выполнение условия (2.7) как строгого неравенства может свидетельствовать либо о целесообразности закрытия, перепрофилирования соответствующего предприятия, либо о недостаточном качестве набора вариантов и необходимости нахождения для него более эффективных вариантов.
Здесь отчетливо проявляется дна из основных проблем, возникающих при выборе хозяйственных решений, а именно: проблема существования и подготовки качественной исходной информации для последующего выбора на ее основе тех или иных решений.
Задание к контрольной работе № 2.
Используя MS Excel, найти решение для задачи целочисленного линейного программирования, соответствующей заданному варианту (см. лабораторную роботу №1). Решить задачу (см. задачу лабораторной роботы №1) с учетом булевых переменных.
Исходные данные транспортной задачи
| Тарифы, грн. шт. | 1-й магазин | 2-й магазин | 3-й магазин | Запасы, шт. |
| 1-й склад | 2 | 9 | 7 | 25 |
| 2-й склад | 1 | 0 | 5 | 50 |
| 3-й склад | 5 | 4 | 100 | 35 |
| 4-й склад | 2 | 3 | 6 | 75 |
| Потребности шт. | 45 | 90 | 50 |
Целевая функция и ограничения данной задачи имеют вид
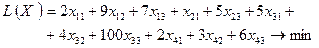
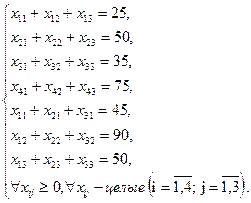 (3.13)
(3.13)
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий транспортной задачи (3.13) и ее решение представлены на рисунках 3.1, 3.2, 3.3 и в таблице 3.4
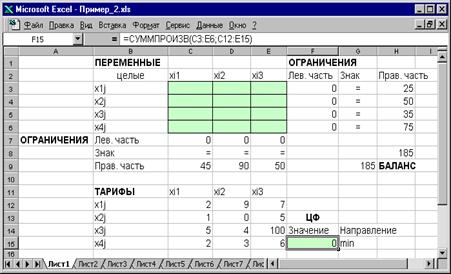
Рисунок 3.1 Экранная форма транспортной задачи 2 (курсор в целевой ячейке F 15)
Таблица 3.5.
Формулы экранной формы задачи (1.5)
| Объект математической модели | Выражение в Excel |
| Переменные задачи | C3:E6 |
| Формула в целевой ячейке F15 | =СУММПРОИЗВ(C3:E6;C12:E15) |
| Ограничения по строкам в ячейках F3, F4, F5, F6 | =СУММ(C3:E3) =СУММ(C4:E4) =СУММ(C5:E5) =СУММ(C6:E6) |
| Ограничения по столбцам в ячейках С7, D7, E7 | =СУММ(C3:C6) =СУММ(D3:D6) =СУММ(E3:E6) |
| Суммарные запасы и потребности в ячейках H8, G9 | =СУММ(H3:H6) =СУММ( C 9: E 9) |
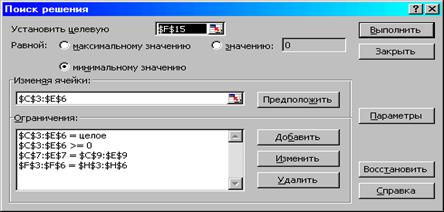
Рисунок 3.2. Ограничения и граничные условия задачи 2
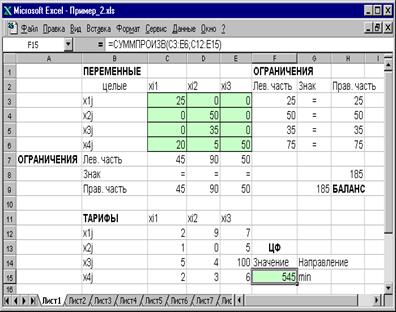
Рисунок 3.3. Экранная форма после получения решения задачи (1.5) (курсор в целевой ячейке F 15)
Задание к контрольной работе № 3.
Используя MS Excel, найти решение транспортной задачи, соответствующей заданному варианту.
Вариант № 1.
| ai \ вj | 700 | 300 | 200 | 400 |
| 900 | 18 | 20 | 14 | 10 |
| 300 | 10 | 20 | 30 | 30 |
| 400 | 16 | 22 | 10 | 20 |
Вариант № 2.
| ai \ вj | 60 | 65 | 75 | 50 |
| 70 | 0 | 4 | 3 | 1 |
| 80 | 4 | 3 | 2 | 2 |
| 80 | 6 | 3 | 5 | 5 |
| 20 | 4 | 7 | 6 | 1 |
Вариант № 3.
| ai \ вj | 100 | 400 | 200 | 300 |
| 100 | 2 | 4 | 2 | 1 |
| 150 | 3 | 1 | 5 | 6 |
| 250 | 1 | 7 | 3 | 5 |
| 500 | 5 | 8 | 6 | 1 |
Вариант № 4.
| ai \ вj | 400 | 200 | 200 | 200 |
| 250 | 6 | 1 | 4 | 2 |
| 300 | 3 | 5 | 1 | 3 |
| 350 | 5 | 6 | 7 | 1 |
| 100 | 2 | 1 | 8 | 5 |
Вариант № 5.
| ai \ вj | 30 | 70 | 50 | 100 |
| 70 | 7 | 5 | 1 | 6 |
| 120 | 5 | 3 | 4 | 9 |
| 20 | 6 | 8 | 7 | 7 |
| 40 | 4 | 3 | 5 | 5 |
Вариант № 6.
| ai \ вj | 75 | 125 | 60 | 140 |
| 80 | 4 | 5 | 2 | 10 |
| 40 | 7 | 3 | 2 | 4 |
| 160 | 3 | 4 | 3 | 5 |
| 120 | 5 | 7 | 9 | 6 |
Вариант № 7.
| ai \ вj | 450 | 400 | 50 | 140 |
| 300 | 7 | 9 | 9 | 5 |
| 150 | 2 | 5 | 8 | 9 |
| 350 | 5 | 6 | 4 | 8 |
| 200 | 3 | 11 | 2 | 3 |
Вариант № 8.
| ai \ вj | 25 | 35 | 45 | 35 |
| 50 | 6 | 8 | 2 | 4 |
| 30 | 7 | 2 | 5 | 4 |
| 40 | 8 | 1 | 7 | 2 |
| 20 | 1 | 2 | 8 | 10 |
Вариант № 9.
| ai \ вj | 60 | 40 | 35 | 65 |
| 45 | 4 | 2 | 3 | 2 |
| 30 | 7 | 5 | 7 | 3 |
| 50 | 2 | 6 | 8 | 4 |
| 75 | 5 | 1 | 3 | 1 |
Вариант № 10.
| ai \ вj | 200 | 100 | 80 | 120 |
| 60 | 2 | 5 | 4 | 2 |
| 140 | 3 | 1 | 3 | 1 |
| 160 | 6 | 3 | 3 | 2 |
| 140 | 3 | 4 | 6 | 0 |
Вариант № 11.
| ai \ вj | 600 | 400 | 200 |
| 100 | 6 | 15 | 9 |
| 400 | 7 | 10 | 16 |
| 700 | 9 | 11 | 15 |
Вариант № 12.
| ai \ вj | 40 | 120 | 40 | 20 |
| 150 | 1 | 1 | 3 | 2 |
| 50 | 4 | 8 | 4 | 3 |
| 20 | 3 | 3 | 2 | 2 |
Вариант № 13.
| ai \ вj | 250 | 250 | 400 | 600 |
| 350 | 8 | 1 | 10 | 8 |
| 650 | 11 | 15 | 11 | 7 |
| 500 | 12 | 7 | 15 | 12 |
Вариант № 14.
| ai \ вj | 700 | 300 | 200 | 400 |
| 900 | 18 | 20 | 14 | 10 |
| 300 | 10 | 20 | 30 | 30 |
| 400 | 16 | 22 | 10 | 20 |
Вариант № 15.
| ai \ вj | 100 | 100 | 400 | 1000 |
| 500 | 20 | 10 | 30 | 50 |
| 800 | 30 | 20 | 30 | 20 |
| 300 | 30 | 50 | 50 | 50 |
Вариант № 16.
| ai \ вj | 450 | 350 | 550 | 650 |
| 500 | 4 | 1 | 3 | 5 |
| 600 | 2 | 2 | 3 | 7 |
| 900 | 4 | 3 | 5 | 3 |
Список используемой литературы
1. Костевич Л.С. Математическое программирование: Информ. технологии оптимальных решений. – Мн.: Новое знание, 2003. – 424 с.
2. Дорохина Е.Ю., Халиков М.А. Моделирование микроэкономики. учебное пособие для вузов/ под общ. ред. Н.П. Тихомирова – М.:Издательство «Экзамен», 2003. – 224 с.
3. Замков О.О., Толстопятенко А.В.,Черемных Ю.Н Математические методы в экономике: Учебник МГУ им. М,В. Ломоносова. М.: ДИС, 2000.- 346 с.
4. Интрилигатор М. Математические методы оптимизации и экономическая теории. М.: Прогресс, 2001. – 300 с.
5. Нейман Дж., Моргенштерн О. Теория игр и экономическое моделирование. М.: Наука, 2003. – 206 с.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ»
Факультет «Экономика, управление и информационные системы в строительстве и недвижимости
Кафедра «Менеджмент строительных организаций»
А.О. Коломыцева
Математические методы и модели в экономике и менеджменте.
Реализация в MS Excel
Учебно-методические материалы к организации самостоятельной работы студентов и выполнения контрольной работы студентов заочной формы обучения
Макеевка 2018
Содержание
Введение 4
Дата: 2019-03-05, просмотров: 373.